TMUA Guides
TMUA Paper 1- Understanding the First Part of the TMUA
Written by: Matt Amalfitano-Stroud
Preparing for the TMUA can feel like a big task due to the two papers required for it. It’s a lot to get ready for, but looking at each paper separately may be useful to pace the workload and increase your revision efficiency. Let’s take a look at Paper 1 to see what you need to know to get a great score!
1/5
WHAT IS THE TMUA?
The Test of Mathematics for University Admission (TMUA) is exactly what it sounds like. Before we get into the nitty-gritty, let’s take a quick look at how the TMUA works.

The Test of Mathematics for University Admission (TMUA) is exactly what it sounds like. The exam is designed to test all the mathematical knowledge you’ve learned so far in different contexts. You will need to answer both pure mathematical questions and scenario-based questions based on logical thinking.
You’ll be taking the TMUA if you’re applying to subjects with a heavy mathematical basis, which could range from pure mathematics to economics or computer sciences.
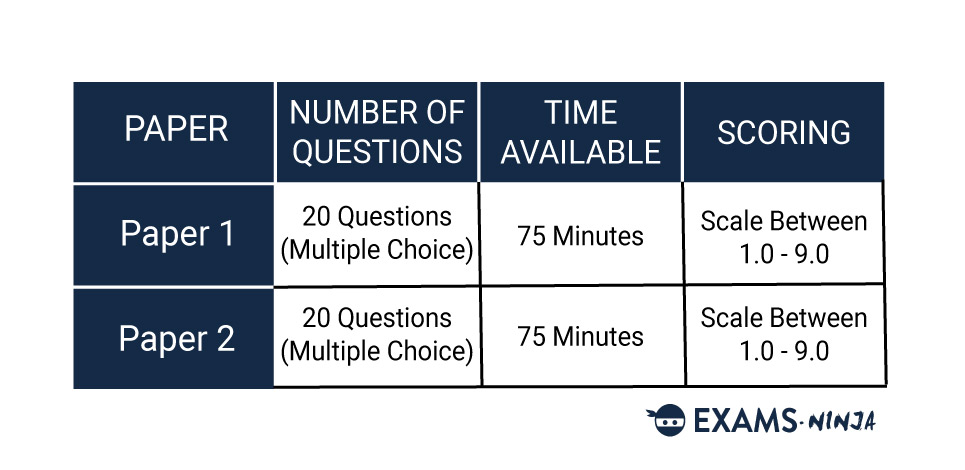
The TMUA consists of 2 papers, both of which are 75 minutes long and are sat back-to-back. Both papers consist of 20 multiple-choice questions and do not allow access to a formulae book or a calculator. Paper 1 will see you answering pure mathematical problems while Paper 2 will require you to use your conceptual knowledge of mathematics in various scenarios.
TMUA Structure
How is the TMUA Scored?
Your result for the TMUA is based on a scale that runs from 1 (lowest) to 9 (highest) and is calculated using the results of both papers. Applicants are not penalised for wrong answers and only receive points for correct answers, so it is encouraged to answer every question.
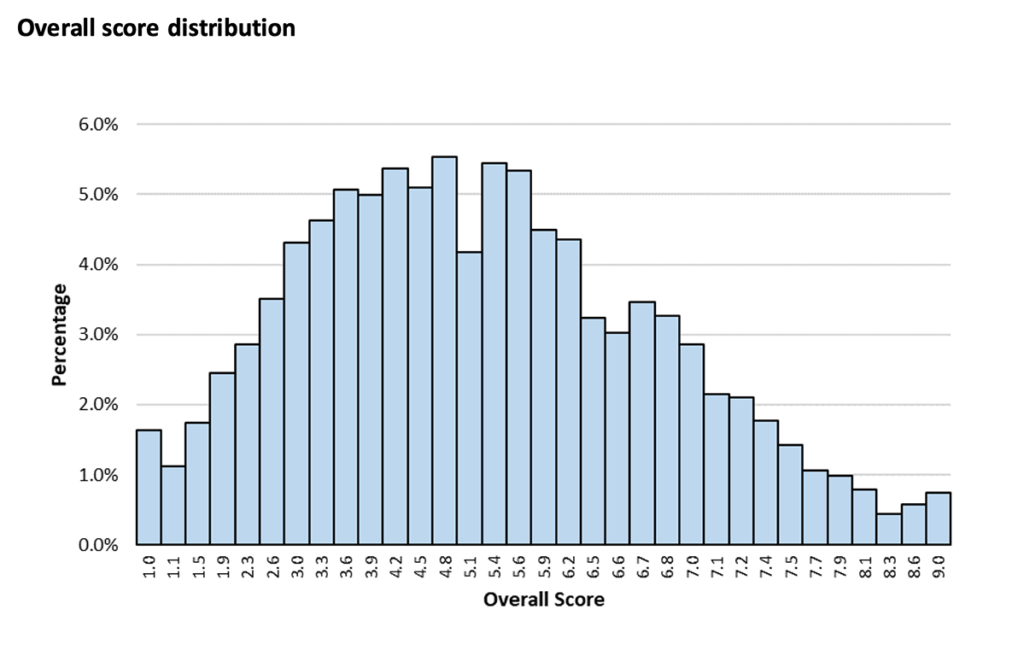
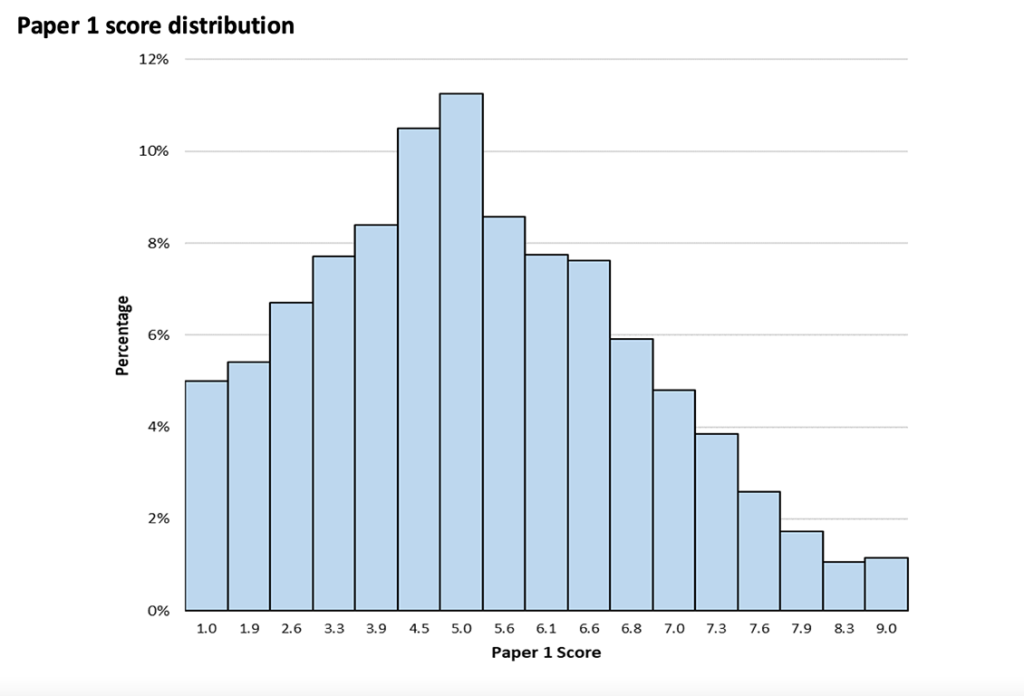
Below you can find the distribution of TMUA results for both Paper 1 and overall results, as reported for 2020-21 by Cambridge Assessment Admissions Testing, the former operators of the TMUA.
As you can see, the most common result was 4.8 with around 5.5% of applicants reaching this score. Paper 1 specifically saw a most common score of 5.0 from around 11% of applicants.
2/5
WHAT TO EXPECT FROM THE TMUA PAPER 1
As we know, each paper has 20 multiple-choice questions. Each question is a purely mathematical problem that will need to be solved using a variety of disciplines that you should have learnt throughout your current education.
Of course, all questions are multiple-choice so you won’t be completely without guidance as to what the answer may be. Each question has a selection of up to eight answers, only one of which will need to be selected. The TMUA is fully computer-based, so all questions and answers are presented on a dedicated testing software.
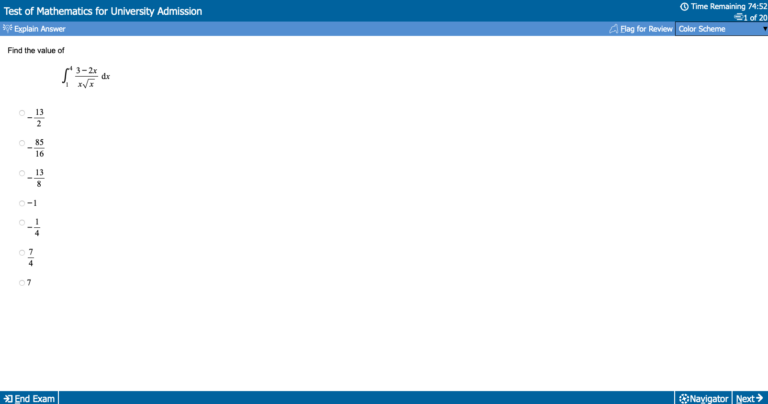
Here’s how a typical question page in the paper is laid out:
The page itself is laid out with a lot of free space, with options to move forward and backward and flag the question you’re currently on, which will highlight that you wish to return to it once you’ve worked through the other questions. You can also see the time remaining for the paper in the top right corner.
You will be given paper to do rough working out, so be sure to bring a pencil with you. Calculators and other supporting materials are not permitted.
There’s a lot to revise for the TMUA, so why not get some help?
With our TMUA Preparation Platform, you can get access to guides and practice questions for all content of the TMUA. Click below to find out how you can optimise your TMUA revision.
3/5
WHAT MATHS IS COVERED IN THE TMUA?
None of what we’ve discussed so far should be too out of the ordinary for you, as Paper 1 is set out like a fairly standard mathematics exam. Most of the mathematical knowledge required for the paper is featured in the Pure Mathematical specification for AS Level Maths and Higher Level GCSE maths, meaning nothing included should be unknown to you. Let’s dive deeper and see what kind of mathematics you’ll actually be taking on!

Numerical Skills & Units
The foundation of all mathematics, you will need to make sure you have the basics down to a tee. This will include the core functions, vocabulary and methods of the following:
- Numeracy
- Conversions
- Index Laws
- Direct and Indirect Proportion
- Ratio Notions
- Number Operations
- Surds and Pi in Exact Calculations
As for units, the required knowledge is fairly simple:
- Standard Units (mass, money, time, length, etc)
- Compound Units (speed, density, pressure, etc)
- Conversions Between Related Units
Algebra and Functions
As a key component of mathematical equations, it shouldn’t come as a surprise that you’ll be answering questions based on algebra.
You’ll need to revise this topic thoroughly as there’s a lot of ground to cover when talking about algebra. Knowledge of the basic formulae and uses are essential, but there are plenty of more complex principles to revise before you enter the exam. These include:
- Laws of Indices for Rational Exponents
- Solving Linear and Quadratic Inequalities
- Algebraic Manipulation of Polynomials
- Simultaneous Equations (with one Linear and one Quadratic Equation)
- Using and Manipulating Surds
- Quadratic Functions and their Graphs
You can more algebra tips, tricks and practice questions in our TMUA Algebra Guide!
Sequences and Series
Sequences can link into a variety of mathematical disciplines, from algebra to geometry. Understanding pattern recognition and being able to express the series of a sequence will be important for your success in both papers of the TMUA. You’ll want to make sure you’re familiar with:
- Arithmetic Series
- Geometric Series
- Binomial Expansion
Geometry
Geometry is another fairly varied subject and can be a favourite among more visual learners. The questions on Paper 1 will rarely be based on solid geometry (three-dimensional) which helps simplify things to a certain degree. However, you will need to know about the following:
- Circle Properties
- Coordinate Geometry
- Angle Properties
- Rotational Symmetry
- Congruence and Similarity
Trigonometry
The branch of geometry focusing on triangles, you’ll need to be sure to give this subject just as much attention as pure geometry due to the number of unique rules at play. Skills needed in this area include:
- Pythagoras’ Theorem
- Rules and functions of Sine, Cosine and Tangent
- Radian Measure
- Simple Trigonometric Equations
Ratio & Proportion
Recently included in the specification, applicants need to have an understanding and ability to use ratios and proportions:
- Scale Factors & Diagrams
- Ratio Notation
- Express Quantities as Fractions
- Apply Ratio to Real Contexts
- Basic Proportion
- Direct & Inverse Proportion
- Fractions within Ratio Problems
- Percentages,& Percentage Change
- Compare Length, Area & Volume with Ratio Notation
- Growth & Decay Problems
Exponentials and Logarithms
Exponential functions and logarithmic functions have an endless amount of real-world applications, so you’ll need to make sure you have a good understanding of how they work for the TMUA, as well as your future career, be it Accountancy, Engineering and many more. Starting with the basics of y=ax, you will also want to revise:
- The Laws of Logarithms, including special cases
- The solution to equations of the form ax = b
Differentiation
Derivatives are a fundamental tool within calculus and have a wide variety of practical uses. You will want to revise the following:
- The Derivative of f (x) as the gradient of the tangent to the graph y=f (x) at a point
- Second-Order Derivatives
- Differentiation of xn for the rational n
- Applications of Differentiation to; tangents, normals, gradients and stationary points
Statistics and Probability
Another highly practical area of mathematics, statistics and probability have a pretty equal balance of numerical and graphical working. When revising, bear these topics in mind:
- Estimates and Measures of Probability
- Venn, Tree and Scatter diagram Construction
- Averages
- Graph and Chart Interpretation
- Data Comparisons
- Data Collection Critical Analysis
Integration
Integration is a tricky topic, but you’ll need to make sure you know it as it will support you with many other areas of maths, including algebra and graphic interpretation. Some key areas to revise are:
- Definite and Indefinite Integration
- Fundamental Theorem of Calculus
- Combining Integrals with Equal or Contiguous Ranges
- The Trapezium Rule
Graphs of Functions
You’ll likely have seen hundreds of graphs in your studies by now, so you should hopefully know how to use them! Remember to revise the following areas:
- Graph Sketching relating to common functions
- Simple Graphic Transformations and Alterations
- Geometric Interpretation of Algebraic Solutions of Equations
- Use of Differentiation and Algebraic Techniques
A fully comprehensive list of everything you will need to revise has been created, known as the TMUA Specification. This will be essential to look through in order to know which formulae, equations and disciplines you’ll need to have revised before you sit the paper.
4/5
HOW DO I PREPARE FOR THE TMUA PAPER 1?
Now you’ve seen what you need to know, your next question will likely be
“How can I memorise all this?”.
While revision isn’t simply about memorising facts, it certainly will play a big part in your exam preparations.
Here are a few key areas that can help with your revision for the TMUA.
1. Make a Revision Plan
Burnout and disorganisation are all too common in exam revision, especially for a topic as complicated and varied as Mathematics. Approaching your revision the wrong way could potentially cost you your place at your dream university, so planning your revision will be a huge benefit to you in the long run.
Your first step could be to create a schedule based on what you realistically think you’ll need and be able to achieve. Every person will have different needs and different ways of learning and revising, so your revision schedule should be unique to you. Think about the areas you struggle with compared to what you’re confident with. While it’s handy to sharpen your skills in every area, there will always be places that require more attention than others, so it’s always best to focus on those to increase your odds of understanding them.
Remember, you’re not a machine! Humans need breaks and downtime no matter how important the task is, so the schedule should take this into account. Burning out in the middle of your preparation could have disastrous results and it’s common knowledge by now that cramming at the last minute does very little to help your chances of success.
If you want to learn more about this, why not check out our TMUA 6-Month Preparation Timeline to find out what you should be doing in every step of the way to the TMUA!
2. Complete Lots of Practice Questions
As you’ve likely heard a hundred times by now, Practise Makes Perfect, and it’s true! Testing your knowledge with actual problems will help you to understand your methodology in a practical way. Whether through textbook examples or questions from previous papers, there’s a multitude of channels to practise your skills.
To help you understand what a correct answer actually means, using questions with worked solutions will allow you to see a full explanation of why an answer is correct and why the other options are incorrect. This is a great tool to utilise no matter your skill level in a certain topic, as you can either confirm your understanding of a solution or learn why you were previously solving the problem incorrectly.
Practice questions can come from a variety of places, including Exam.Ninja’s TMUA preparation platform, which features over 500 exam quality questions to attempt, each with worked solutions.
3. Take Past Papers
Everyone has different ways of learning, but everyone also sits the paper in the same way, so why leave anything open to surprises? Taking a past paper in a controlled environment is helpful in a variety of ways.
Sitting the paper within the 75-minute time limit will give you an idea of how you’ll perform under pressure and will allow you to adjust your methods to complete the exam on time. It will also be important to allow yourself some extra time within the 75 minutes to go over your answers, perhaps around 5-10 minutes. It’s easy to make mistakes when in a stressful environment but checking your work gives you a much better chance of catching out any mistakes before it’s too late.
Completing practice questions is a fantastic revision technique, as we’ve already discussed, but completing official past papers will give you an accurate idea of the kind of questions you can expect to see, as well as the layout of the exam. All of the TMUA past papers are available on our site, so be sure to check them out!
Since the TMUA is now a computer-based test, you should also be sure to try out the official practice test that uses the UAT testing system. This test gives you a realistic look at how the exam works, but be aware that the question selection is very limited.
Get access to hundreds of exam quality TMUA practice questions.
The TMUA Preparation Platform is the most effective way to revise for your exam! You can get access to over 500 practice questions, each with a worked solution, as well as 5 full past papers to complete. Click below to try it out for free!
5/5
TMUA PAPER 1 PRACTICE QUESTIONS
Let’s take a look at some example questions, complete with worked examples. These should give you a clearer idea of what your exam questions will look like.
TMUA Practice Question 1
Given that, in the expansion of (3x + b)7, the coefficient of x4 is the same as the coefficient of x2 in (3b + x)4, find the positive constant b.
A) 2/105
B)105/2
C)107/3
D) 3/107
E) 109/4
The correct answer is A.
In the first expansion, the coefficient of x4 is given by (7 4) 34b3 = 2835b3 and in the second, the coefficient of x2 is (4 2) (3b)2= 54b2, and equating, we see that b = 54/2835 = 2/105.
TMUA Practice Question 2
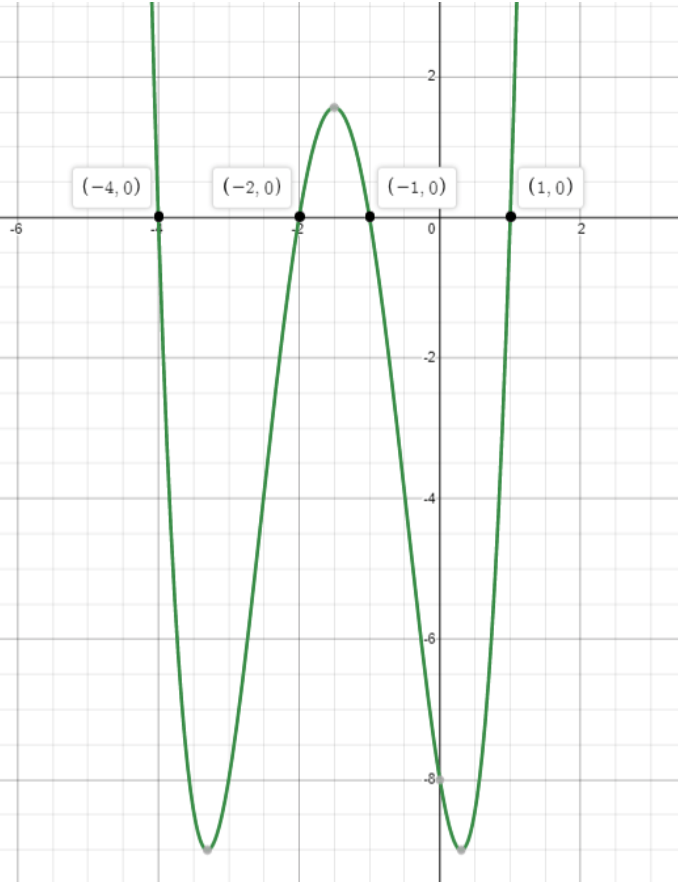
In which of the following ranges is (x2 – 1)(x + 2)(x + 4) > 0?
A)-2 < x < 1
B) -1 < x < 2
C) -2 < x < -1
D) x ≥ 1
E) x < -3
The correct answer is C
We may factorise the function as (x -1)(x -1)(x + 2)(x + 4), which allows us to graph it.
TMUA Practice Question 3
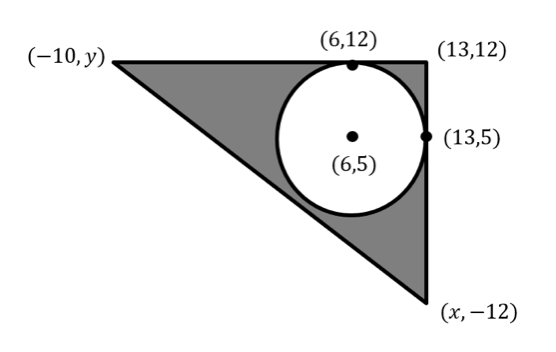
A circle has the equation x2 – 12x + y2 – 10y +12 = 0, and is tangent to two sides of the triangle. Some coordinates on the triangle are labelled.
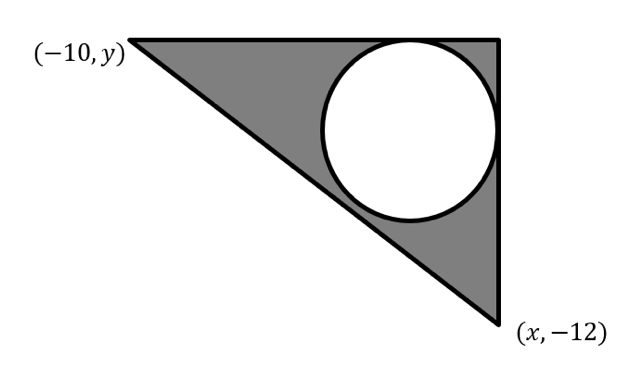
Find the exact value of the shaded area.
A) 305
B) 528 – 49π
C) 552 – 492π
D) 4290 – 362π
E) 276 – 49π
F) 169 – 36π
The correct answer is E.
Find the equation of the circle by completing the square:
x2 – 12x + y2 – 10y + 12 = 0
(x – 6)2 – 36 + (y – 5)2 – 25 + 12 = 0
(x – 6)2 + (y – 5)2 = 45
Radius + 7 centre (6, 5)
Area of the triangle = 1/2 x 23 x 24 = 276
Circle Area = 49π
Shaded Area + 276 – 49π
TMUA Practice Question 4
On a cheese farm, the mass of cheese produced and measured on the scales T minutes after the cheese machine has started, is G grams. For any time, the rate of cheese production is proportional to the mass of cheese formed. However, cheese is removed from scales at a constant rate of 10 grams per minute. When the mass of cheese on the scales was 150g, and the rate of change of cheese weight on the scales was 90 g/minute.
When the rate of change of mass of cheese was 50g/min, what was the mass of cheese formed?
(You may find it beneficial to create a differential equation to show this.)
A) 150
B) 50
C) 40
D) 90
E) 0.3
F) 160
G) 60
The correct answer is D.
The rate of change of cheese mass equals the rate of formation – rate of removal of cheese from the scales
dG/dT = kG -10
90 = 150k -10
k = 2/3
dG/dT = 50, G = 90.
TMUA Practice Question 5
I have 2 blue balls and 3 red balls which I will throw into 5 indistinguishable boxes. Assuming I don’t miss, how many distinct situations could I be in after all the balls are thrown?
A) 14
B) 55
C) 32
D) 16
E) 8
F) 4
G) 53 + 52
The correct answer is D
This is a problem about counting. The boxes are indistinguishable, which means we only care about how the balls are distributed, not specifically which boxes they are in.
A good way to approach these is to have an order to the counting. We shall do it based on how many boxes are empty at the end:
0– This is only true if there is 1 ball in each box, and there is only one way to do this.
1– There must be 2 balls in 1 box and 1 in the other 3. The 2 balls could both be blue, both be red, or be 1 of each.
2– There are two possibilities here, a 3,1,1 split, or a 2,2,1 split. In the former case, the 3 balls could be all red, 2 red 1 blue, or all blue. Either way they uniquely determine the other balls. In the latter case, we consider where the 2 blue balls are; they could be in the same box, one could be in each of the boxes with 2 balls in, or one could be in a 2 box and the other in the 1 box. As there are no other ways to distribute the blue balls, this is an exhaustive list.
3 – All balls being only in 2 boxes means they are split 1,4 or 2,3. In the former, there are 2 possibilities, the single ball is red, or it is blue. In the latter, there are 3 possibilities for the box with 2 balls in, RR, BB or RB, but no matter what this also determines what is in the other box.
4 – Only one way, all the balls are in the same box
Summing these possibilities, we have 16 ways.
TMUA Practice Question 6
Let f(x) = ax2 + bx2 + cx -75 for some integers a, b, c . f (3/4) = f(-5) = 0 and f(x) = 0 for only these values. What is the mean of the numbers a, b, c?
A) 50
B) -35
C) 115/3
D) 35
E) -43/3
F) 12
The correct answer is C.
Instead of trying to calculate sums involving 53, we can treat this like a factorisation problem. We are told that (4x – 3) (x – 5) are the only roots, so we can deduce their powers in the factorisation of f(x) by looking at the constant term. 75 = 52 x 3 which means our polynomial must be equal to (4x – 3) (x – 5)2. From here, we can simply expand this and find our answer; (4x – 3) (x – 5)2 = (4x – 3)(x2 – 10x + 25) = 4x2 + 53x2 + 58x – 71. Then our average is:
4 + 53 + 58/3 = 115/3 .
TMUA Practice Question 7
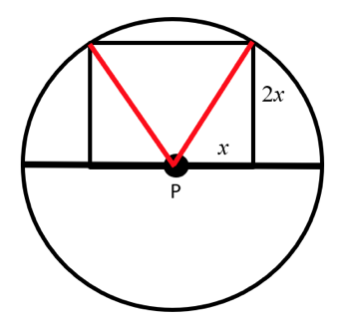
A circle, with a diameter of 4cm, contains a square with two vertices on the diameter of the circle, and 2 vertices on the circumference of the circle, as shown below.
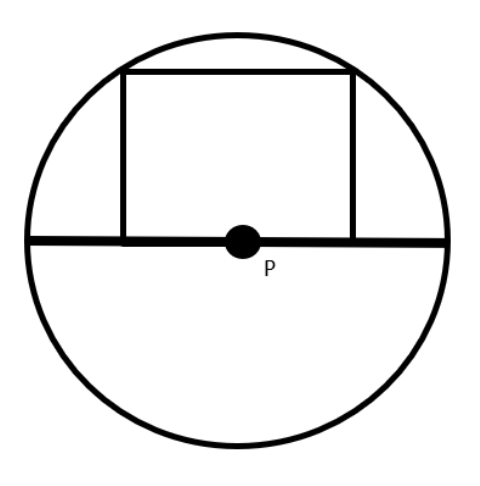
Calculate the area of the square.
A) 4/5
B) 16/5
C) 4
D) 7/2
E) 9/2
F) 17/4
G) 64/5
The correct answer is B
You can form two triangles, using two radii, each of length 2cm.
We can label the length of each side of the square as 2x, so the distance from P to the vertex is x
Using Pythagoras’ theorem:
22 = x2 + (2x)2
4 + 5x2
x2 = 4/5
Area of square:
4x2 = 4 x 4/5 = 16/5
TMUA Practice Question 8
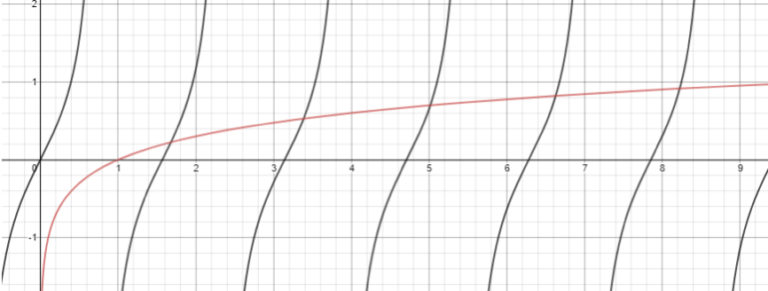
How many solutions does the equation cos2x x logx + sin2x have in the range 0 < x < 3π?
A) 0
B) 3
C) 5
D) 6
E) 7
The correct answer is C
Note that we may divide through by cos2x to obtain the equation logx = tan2x. We have to be careful though that we have no solutions when cos2x = 0, but this is clear since if cos2x = 0 then sin2x = ± 1 . Now draw a graph of logx, and of tan2x and count the number of intersections in the range. There are 5.
This should give you just a good idea of what quality practice questions should look like. Attempting as many of these as possible will help you increase your skills in every area of maths in a highly practical way.
Keep an eye out for more TMUA practice questions on Exams.Ninja coming soon!
You should now have a good understanding of what to expect now, so the next step is to get on with your preparations! Don’t forget about Paper 2, which you will need to take directly after Paper 1. A lot of knowledge thankfully overlaps, the differences come more from the context of the questions you’ll need to answer.
The key to succeeding in the TMUA is to understand the core principles of advanced maths, so you’ll want to plan your revision and make the most of your time and resources.
Combine all your TMUA preparation in one comprehensive package.
Exams.Ninja’s TMUA Preparation Platform allows you to optimise all areas of your revision in one easy to use platform. With the Preparation Platform, you’ll get access to:
Training Temple- exclusive tips, life-saving revision notes and over 100 expert tutorials to guide you every step of the way.
Practice Dojo- over 500 practice questions, each one matching the difficulty of real TMUA questions with fully worked solutions to help you understand everything you need to know.
Exam Arena- Attempt 5 full TMUA past papers in a real exam scenario. See where you’re at and how you will do on the big day.
Start preparing for the TMUA today to maximise your chances of success.