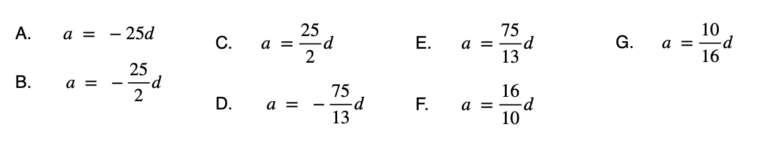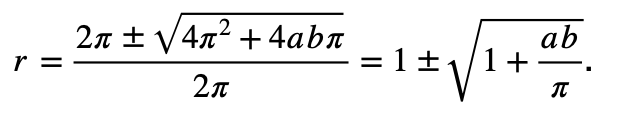TMUA Guides

TMUA Paper 2 - The Definitive Guide to Paper 2 of the TMUA

Written by: Matt Amalfitano-Stroud

The TMUA is a tough exam, as you probably already know. With two papers covering two different styles of questions, it can be overwhelming to try and study not just the pure maths but also the techniques to answer each paper. It’s too much to do in one go, so we’ve created a guide dedicated to Paper 2 of the exam to help you get through your revision one paper at a time. Let’s take a look at the essential info you’ll need to get a great score!

1/5

WHAT IS THE TMUA?

It’s important to know everything that you can about the exam you’re taking, so firstly we’re going to go over the basics you’ll need to know to prepare.

The Test of Mathematics for University Admission (TMUA) is pretty self-explanatory, it’s a university admission mathematics test! In the UK, 5 universities will use your TMUA results within your application as a demonstration of your academic abilities either as a requirement or an option. As you’d expect, you’ll be taking this test if you’re applying for any mathematics course at these unis, although there are a couple of additional courses as well, including Computer Science at the University of Cambridge and Economics, Finance and Data Science at Imperial College London.

How does the TMUA work?

The TMUA is designed to test you on your knowledge of the pure mathematics that is covered in GCSE and A-Levels (or their equivalents). You’ll be answering both pure mathematical questions and scenario-based questions based on logical thinking that rely on your ability to use context in problem-solving and evaluation.

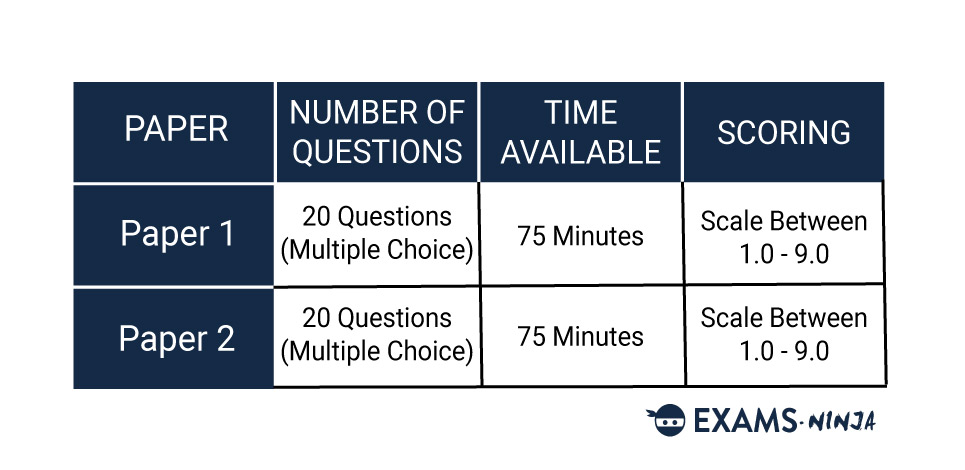
You will have 2 papers to complete in the exam, both of which are 75 minutes long and taken one after the other. There are 20 multiple-choice questions in each paper, featuring pure mathematical problems in Paper 1 and more contextual/scenario-based questions in Paper 2. Both papers are computer-based, though paper is provided for rough working out.

TMUA Structure

How is the TMUA Scored?

The TMUA is scored on a scale from 1 (lowest) to 9 (highest) and is calculated using your results from both papers. It’s important to note that the examiners only use positive marking, meaning your score can only increase with correct answers and won’t decrease from incorrect answers. Therefore, you should be sure to answer every question, even if you run out of time to properly attempt to solve some.

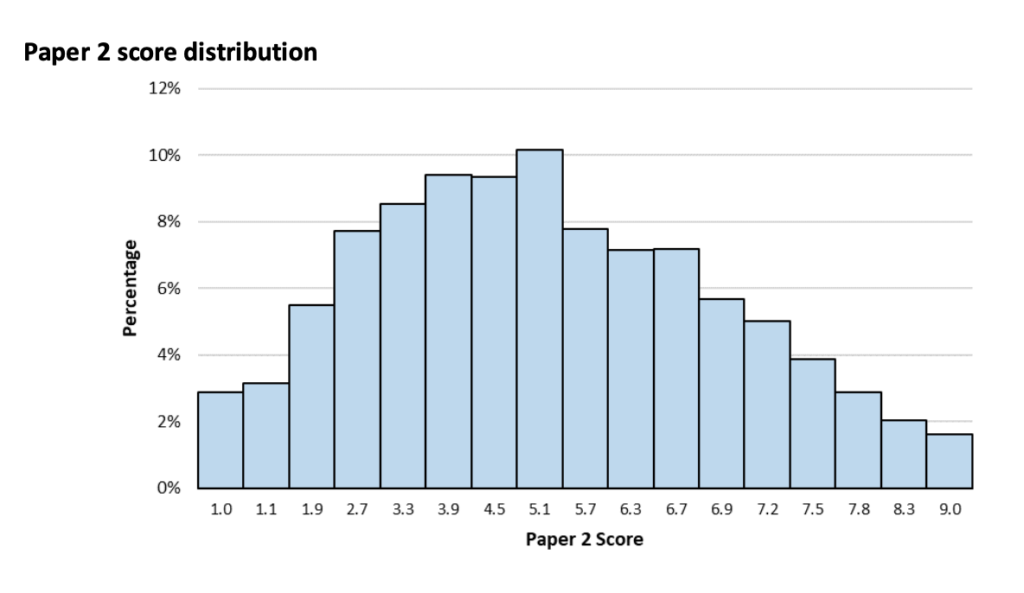
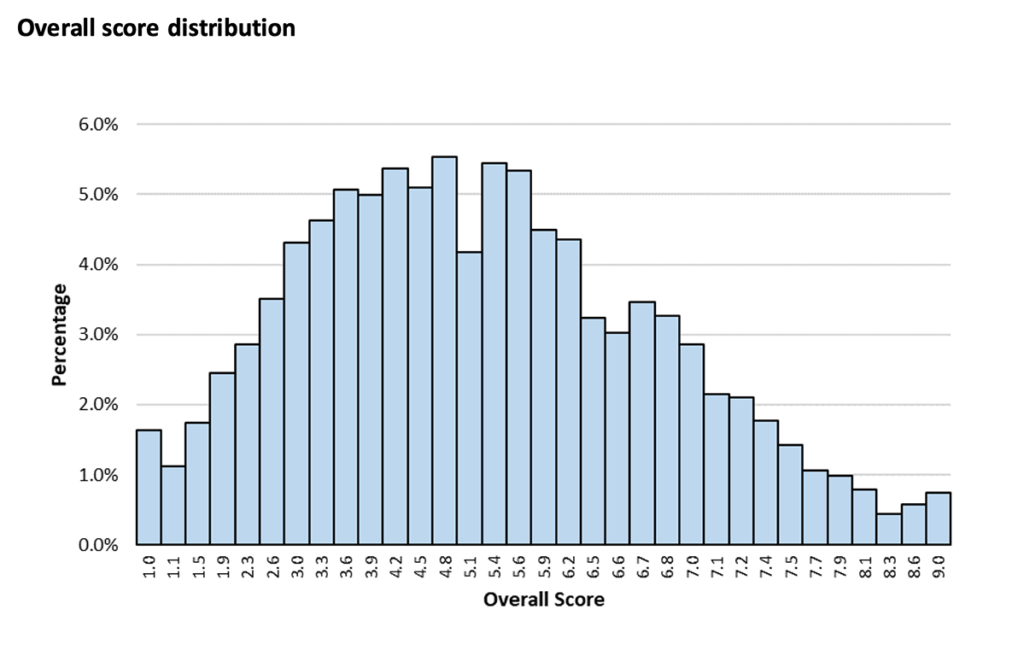
Below you’ll find the distribution of TMUA results for Paper 2 and overall results, as reported for 2021:

What is a Good TMUA Score?

It is reported that approximately one-third of candidates score about 6.5 in the exam, which is generally considered a good minimum score to aim for. You can see that the majority of candidates (over 10%) scored 5.1 in Paper 2.

Remember, Paper 2 is only half the story. To learn more about Paper 1 of the TMUA, check out our Definitive TMUA Paper 1 Guide.

Want to get a head start on your TMUA prep?

Exams.Ninja is here to help with our TMUA Preparation Platform! When you sign up, you’ll have instant access to hundreds of practice questions and loads of past papers! Set up your free account today to start preparing!

2/5

WHAT TO EXPECT FROM THE TMUA PAPER 2

It’s time to take a look at the paper itself! Paper 2 has a very different style of questions from the first paper, so you’ll want to make sure you understand how to they work.

At first glance, both papers of the TMUA seem pretty identical. 20 multiple-choice questions, 75 minutes to finish and each paper even covers the same mathematical disciplines:

The presentation is the same as Paper 1, so the differences come down to the question content. Remember, a lot of the questions in Paper 2 are scenario-based, meaning there’s more information to consider than the pure maths of the first paper. While not every question is as wordy as this one, you will still need to be prepared with using this extra information when answering the questions.

Exams.Ninja Tip

It may sound obvious, but read the question properly! Longer questions have more elements that can trip you up if you don’t read them properly, so you need to be careful.

During your preparation, you should take some time to revise your question reading, as this will allow you to learn the tricks that these questions sometimes try to pull. During the actual exam, you should read the question as many times as you need to until you understand exactly what it’s trying to ask. If you need to, move forward and come back to the question when you’re more comfortable with answering it.

However, this isn’t to say you’ll need to be reading or writing essays! All the questions are still multiple choice and answering these kinds of questions correctly is still going to require you to solve the pure mathematical problem that’s at the centre of the question. Some of the questions in Paper 2 won’t even have a large amount of context and will feel very similar to Paper 1’s questions. So it’s not going to feel like taking a completely different exam, it’s just a matter of reading the words of the question carefully to decipher the answer.

As we said, nothing’s really changed from Paper 1 in terms of how questions are laid out. Questions are displayed one at a time with up to 8 answer options available for you to click on. You have the option to move to the next question, the previous question, flag the question you’re on or end the exam.

Flagging will highlight the question so that you can return to it if you have time (this can be seen on the review screen that is available once you’ve gone through all 20 questions). In the top right corner, you will find a timer displaying how much time is left for the paper. No calculators are permitted during either paper in the test.

3/5

WHAT'S COVERED IN THE TMUA PAPER 2?

All the mathematics that you have learnt so far will be tested in this paper, but you’ll also need to prepare your abilities in mathematical arguments. Let’s take a look at what that means.

The TMUA is a test of everything that you have learnt during your education so far, so don’t expect anything that you’ve never seen before. However, Paper 2 will be testing you on your critical thinking and reasoning abilities in regards to mathematics, which is an area you may not have as much experience in.

First of all, let’s cover the pure mathematics that you’ll need to know. Luckily, the maths you’ll need to know is exactly the same as Paper 1, so there isn’t any additional or more advanced techniques to revise. Let’s quickly run through Everything you’ll need to practice:

Numerical Skills

The most basic form of mathematics, knowing these fundamentals will be essential to your success:

Numeracy
Conversions
Index Laws
Direct and Indirect Proportion
Ratio Notions
Number Operations
Surds and Pi in Exact Calculations

As for units, the required knowledge is fairly simple:

Algebra and Functions

This is another key component of maths, so you’ll need to ensure you have a good understanding of how to use it in a variety of question types.

Knowledge of the basic formulae and uses is a bare minimum, but at this level, you’ll want to be aware of the more complex principles involved in algebra. These include:

Laws of Indices for Rational Exponents
Solving Linear and Quadratic Inequalities
Algebraic Manipulation of Polynomials
Simultaneous Equations (with one Linear and one Quadratic Equation)
Using and Manipulating Surds
Quadratic Functions and their Graphs

Check out our full TMUA Algebra Guide for loads of tips, tricks and practice questions!

Sequences and Series

Sequences are a very versatile area of mathematics, being used in all sorts of question types. You’ll need to understand pattern recognition and sequence series in order to successfully solve a lot of the questions the TMUA will throw at you. You need to be familiar with:

Geometry

Geometry’s another big one, and pretty different from what we’ve covered so far due to its reliance on visual shapes. You’re unlikely to be answering questions on solid geometry (three-dimensional), but you are going to need to know about the following:

Trigonometry

This one’s fairly similar to geometry, but with a focus on triangles. There are a lot of different disciplines and rules, however, so there’s just as much to revise here as standard geometry! These will include:

Ratio & Proportion

One element that was recently included in the specification is Ratio and Proportion. In the test, you’ll need to have a good understanding of the following:

Scale Factors & Diagrams
Ratio Notation
Express Quantities as Fractions
Apply Ratio to Real Contexts
Basic Proportion
Direct & Inverse Proportion
Fractions within Ratio Problems
Percentages,& Percentage Change
Compare Length, Area & Volume with Ratio Notation
Growth & Decay Problems

Exponentials and Logarithms

Exponential functions and logarithmic functions are incredibly useful in real-world scenarios, which is important to note when revising Paper 2 due to its focus on contextual questions. Starting from the basics of y=ax, you’ll also need to revise:

Differentiation

Derivatives are a major part of calculus and have many practical uses. You should be revising:

Statistics and Probability

This is perhaps the most contextual area of mathematics, given that all questions are entirely dependent on context. Be ready to see plenty of this in Paper 2 by revising:

Estimates and Measures of Probability
Venn, Tree and Scatter diagram Construction
Averages
Graph and Chart Interpretation
Data Comparisons
Data Collection Critical Analysis

Integration

Integration is a hard one to learn, but it’s also important to understand as it will support you with many other areas of maths, including graphic interpretation and algebra. Make sure you understand the following:

Graphs of Functions

Graphs are incredibly common in mathematics, so using them should be second nature by now! Even still, you should prepare yourself for the following:

That covers the pure mathematics, but for Paper 2 there’s more to know! As we’ve already discussed, Paper 2 will be testing you on your ability to think mathematically in an actual scenario rather than simply solving problems in a vacuum. There are a few extra skills that you’ll need to brush up on, which we’ll take a look at now:

The Logic of Arguments

Compared to many other types of context-based problems, mathematics will almost always have an objectively correct solution. When making a mathematical argument then, you will always need to present a Logical Argument.

You’ll need to be able to use mathematical logic in fairly simple situations, such as “if X then Y” or “X only if Y”. The basis of the core maths will be the same as what you’re used to, but you will need to present your answer in a more logical manner. As a basic example:

If x is odd, then x + 1 is even.

Once this argument is made, your job will then be to provide proof.

There are various terms to make sure you understand before entering the exam, including true, false, necessary, sufficient, converse and contrapositive. You’re likely familiar with most of these terms, but it’s incredibly important to understand them in a mathematical context.

Exams.Ninja Tip

In a broad sense, there are two types of arguments you can make; deductive and inductive. Deductive arguments, or reasoning, will involve you forming your answer from two or more statements that are perceived as fact. Inductive arguments on the other hand rely on implication and hypothetical patterns, meaning the point is not fully confirmed by fact but instead is assumed by the available evidence.

In mathematics, you’re almost always going to need to provide proof of your argument, so you will always need to present your answer in a deductive way, offering statements and evidence to said statements. There’s a time and place for assumptions in mathematics when providing evidence is impossible, but the TMUA is unlikely to put you in that kind of situation. After all, the questions are still multiple-choice, not full essays!

Mathematical Proof

As we’ve already seen, providing sufficient proof is going to be the key to the success of your argument. Getting this proof isn’t as simple as just finding the solution, however. To provide sufficient proof in a mathematical context means you’re going to need to show every step of your process (very similar to our worked solutions, which you’ll find in a little bit!).

With the proof found, you’ll need to be able to present it in an easily consumable way. Examples of this would be direct deductive proof (for example, since X, therefore Y), proof by contradiction, proof by cases and disproof by counter-example. You should also understand how to deduce implications from statements, rearrange arguments in order to create a proof of a statement and make and justify conjectures based on small cases.

Due to the exam being multiple-choice, your score isn’t going to come from creating arguments from scratch but recognising all these elements in the arguments you are given. However, these are all valuable skills to have for your future studies and beyond, so be sure to practice!

Identifying Errors

Some of the examples you’ll find within the TMUA questions will have errors, but that’s not an error in itself! These questions are testing you on your critical abilities within mathematics, and a big part of that is identifying errors in another person’s work.

These errors will come in the form of the purported proof of a scenario, which has purposely been solved incorrectly. When you’ve identified an error, there are several steps that you’ll need to take. Firstly, it’s important to understand how this incorrect conclusion has been reached. These solutions aren’t picked out at random but are designed to be the result of a mistake within the working out of the solution. It’s your job to backwards engineer the proof and identify what the original person had done to reach their conclusion.

Most of the time, you’re also going to need to find the correct solution to the problem. This should be as simple as just working it out, and if you’ve already found the error that was originally made, the solution will come to you by correcting that mistake.

The TMUA Syllabus is the official resource from the examining body that outlines everything that both papers of the TMUA will cover. Make sure you go through it extensively as it will help with your revision down the line.

4/5

HOW CAN I PREPARE FOR PAPER 2?

The good thing about revising for the TMUA is that a lot of your knowledge from Paper 1 will be transferable to Paper 2. Let’s look at what you can do to perfect your revision techniques for the exam and what you should specifically be doing to prepare for Paper 2.

1. Plan out your Revision

Any effective revision starts with a well laid-out plan! The TMUA covers a lot of different areas of mathematics so there’s a lot to focus on when revising. However, having a schedule of what you’re going to do and when will be extremely beneficial both short and long term.

If you’ve ever tried revising without a plan before, you’ll know how difficult it is to motivate yourself to start as it feels like an endless task. With a schedule, you’ll know exactly how long you’ll be revising for and will give you something to aim for. That’s not to say that you need to follow your plan to the exact second, but having an idea of how long you’ll actually be studying for will do wonders for your motivation!

Another major benefit is being able to focus your revision on the areas you need the most help with. Of course, you should take some time to go over everything, especially when it comes to practice questions, but it’s only natural to dedicate more time to the things you struggle with. Planning this in the form of a schedule will allow you to get on with your revision straight away instead of deciding what you need to cover.

Lastly, your schedule will need to include downtime. Trying to revise without any breaks isn’t going to do you any good and taking them at random points is likely to increase procrastination and waste valuable study time. Structured breaks on the other hand will help you determine your limits and can act as a reward for particularly difficult tasks.

There’s plenty more to learn about this, so be sure to check out our TMUA 6-Month Preparation Timeline to find out how you can utilise your time effectively!

2. Know your Weaknesses

As we’ve already mentioned, your revision plan should give you extra time to study the areas that you struggle with, but how do you determine what those areas are?

For some, it may be as simple as knowing what they find difficult, but usually, it’s more complex than this. You may be confident in certain topics until you find that your knowledge was actually not as in-depth as you thought. The worst-case scenario is finding this out during the actual exam!

Therefore, you should try to practice every area of mathematics covered by the TMUA before you start your full revision schedule. By trying out different questions, you’ll soon find out what comes naturally to you and what you aren’t as confident in. This will also be a great way to track your progress, as you’ll be able to compare your performance in this area before and after you’ve revised.

3. Answer Questions!

As with any examination, you’re going to want to practice the kinds of questions you’ll find when you sit the actual paper. Practice questions and mock papers are by far the most effective way of doing this, as they will be designed to emulate real exam questions.

When looking for practice questions to answer, try to find ones with worked solutions (such as the ones included with the Exams.Ninja TMUA Preparation Platform). If you get a question incorrect, finding out how the correct answer is solved will be extremely helpful to avoid making the same mistake again. Even if you get the answer correct, it’s still good to confirm how the solution should have been reached. After all, you may have come to the correct conclusion with the incorrect method, and you don’t want to rely on that kind of luck in the actual exam!

When you’re feeling confident, it’ll be time to attempt a full mock exam. You should always try at least one past paper in actual exam conditions, as you’ll want to know how you perform under pressure before you enter the exam. If you didn’t perform as you would have hoped, then you’ll still have time to improve your exam techniques. You can access all of the TMUA past papers here.

One thing that is essential to try out is the official TMUA practice test offered by UAT. This practice test uses the platform that the actual test will be run on, so it’s a great opportunity to get to grips with the system before sitting the real thing. However, be aware that the question selection is very limited.

4. Go Above and Beyond

Section 2 of the TMUA will touch on concepts that you may not have much experience in. Creating logical arguments and reviewing solutions aren’t covered too much within a typical maths syllabus during GCSEs or A-Levels, so these concepts may seem foreign to you. Therefore, your revision and practice should go beyond pure mathematics.

Argument and reasoning skills are needed in a wide variety of topics, from law to science, so why not study some of these areas? You may not understand the finer details, but you should begin to understand the key elements of a quality argument!

Practice questions are always great, as we’ve established! But answering multiple-choice questions will limit how much you are actually able to understand these concepts. Therefore, you should try to seek out longer form questions. If you can create an argument yourself, or thoroughly review a peer’s argument, then you’ll have absolutely no issues with understanding the more simple arguments presented to you in the TMUA!

Exams.Ninja is the ultimate resource for TMUA revision!

With over 100 tutorials, more than 500 fully explained questions and five full TMUA past papers, our TMUA Preparation Platform gives you everything you need to sit both papers with confidence!

Try it for free today to see how you can boost your TMUA score.

5/5

EXAMPLE TMUA PRACTICE QUESTIONS

We’ve covered a lot of information here, but how much of it can you put into practice? Have a go at a few practice questions below and get a better understanding with the fully-worked solutions.

TMUA Practice Question 1

If p is a prime number, which of the following must be true?

I. p is odd

II. p is not divisible by 5

III. p is not divisible by 6

A) I only

B) II only

C) III only

D) I and III only

E) II and III only

The correct answer is C.

Recall the definition of a prime – a positive integer whose only positive factors are itself and 1. I is false – 2 is a counterexample. II is false – 5 is a counterexample, it is prime and divisible by 5. III is true – no prime is divisible by 6, since then it must be divisible by both 2 and 3, neither of which can be p or 1.

TMUA Practice Question 2

A large circular room has 2020 light bulbs attached to the edge. Each light bulb has a switch below it, that controls the state of the two adjacent light bulbs to it. Given that all the light bulbs start off, how many can be turned on at once?

A) 1010

B) 1515

C) 2018

D) 2019

E) 2020

The correct answer is E.

Consider a set of four bulbs. Let 1 denote an on bulb and 0 an off. We start in 0000. Hit the second switch – 1010, now hit the third – 1111. As 2020 is a multiple of 4 this strategy can turn on all the bulbs.

TMUA Practice Question 3

In an arithmetic sequence, the sum of the first 10 terms equals the sum of the first 16 terms. Find the relationship between the values of a and d.

The correct answer is B.

Sum of the first 10 terms = 5(2a + 9d)

Sum of the first 16 terms = 8(2a + 15d)

10a + 45d = 16a + 120d

-6a = 75d

a = -(25/2)d

TMUA Practice Question 4

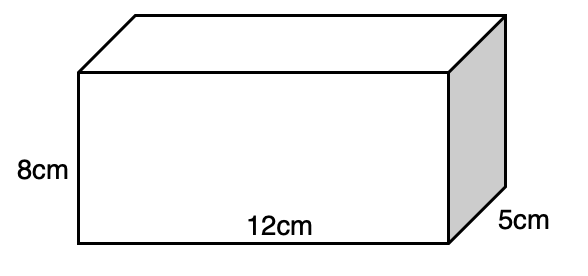
John has a baguette that he is trying to store in his rectangular bread bin, shown below.

If his baguette 17cm long (you may ignore the width/height) – What is the length of baguette he must cut off in order to be able to fit his baguette in the bread bin exactly?

None – the baguette fits in the breadbin and could be longer.
None – the baguette fits in the breadbin exactly.
2cm
17 – 3√3 cm
17 – √177 cm
17 – √233 cm

The correct answer is F.

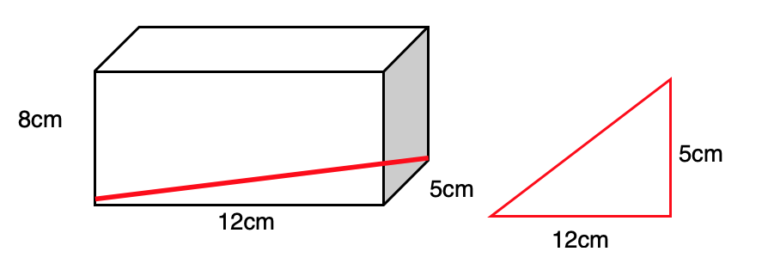
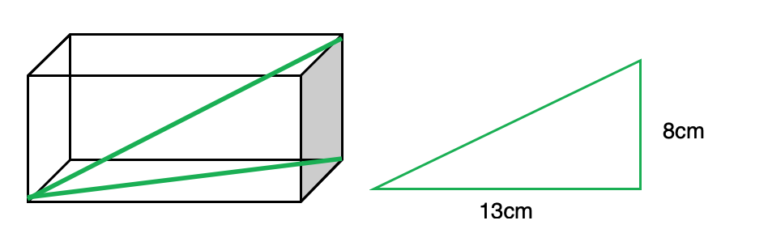
This is a 3D Pythagoras Question.

Use pythagoras’ theorem to see that

12² + 5² = 13², therefore the hypotenuse is 13cm long

Here the hypotenuse is √233. The candidate should recognise that this is just over 15cm.

The answer is 17 – √233

TMUA Practice Question 5

Consider a circle with a kite inscribed in it. Let the centre of the circle be on the positive y-axis and both the circle and kite pass through the origin. Let the short side of the kite be a and the long side be b. The kite also has the y-axis as a line of symmetry.

The area between the kite and the edge of the circle is equal to the perimeter of the circle.

What values can ab take such that there is only 1 circle for which this is true?

A) ab < 2π

B) ab > 2π

C) ab = 2π

D) ab = 12π

E) ab ≠ 2π

The correct answer is G.

As the y-axis is a line of symmetry, we know that the angle between sides of length a & b is a right angle (angles in a semicircle). Thus, we know the area of the kite is 2 x 1/2absin 90 = ab. Thus, our equality states πr² – ab = 2πr. This is a quadratic in r which has solutions:

While it is tempting to say that this has one solution when the discriminant is zero, ab must be positive, so the discriminant is never zero. It is even more tempting to say that this means there are no solutions for ab. However, 1 + (ab/π) > 1, because ab is positive, which means one of the solutions for r is negative. As this is impossible, in fact there is always only 1 solution for r, for any value of ab.

TMUA Practice Question 6

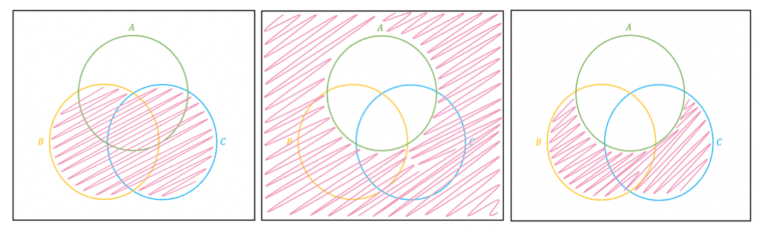
There are 3 events, A, B and C, which are not mutually exclusive. Which of the following is equivalent to the probability that A does not happen, but one of C and B does happen?

A) P((B ∩ A) ∪ (C ∩ A))

B) P((A^C ∪ B) ∩ (A^C ∪ C))

C) P(B ∪ (C ∩ A))

D) P(A^C ∪ B ∪ C)

E) P((B ∪ C) ∩ A^C)

F) P(A^C ∩ B ∩ C)

The correct answer is E.

A Venn diagram shows this the most quickly. The shaded areas below are, respectively,

The event in question is outside the A circle, and inside one of the two other circles (the shaded region in the right hand picture). This is equivalent, as you can see, to the intersection between B ∪ C (left hand picture shaded region) and A^C (middle picture shaded region).

TMUA Practice Question 7

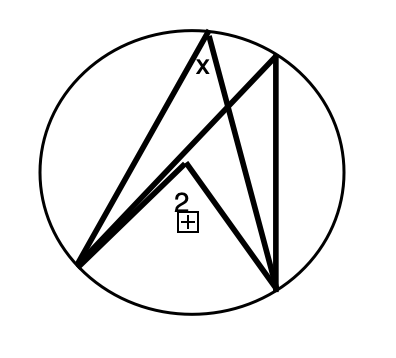
Cisco is trying to prove the circle theorem that angles from the same arc in the same segment are equal.

Which of the following circle theorem rules should he use?

A) “The angle at the centre of a circle is twice the angle at the circumference of the circle from the same arc”

B) “the angle formed in a semicircle is always a right angle”

C) “opposite angles of a cyclic quadrilateral add up to 180 degrees”

D) “two tangents drawn from a point to a circle are equal”

E) “The angle between a tangent and a chord is equal to the angle at the circumference in the alternate segment”

F) “the perpendicular line from the centre of a circle to a chord bisects the chord”

The correct answer is A.

You can see from this diagram that the rule from A is the correct one to use.

TMUA Practice Question 8

Consider the following proof by induction that 3 x 7ⁿ + 6 is divisible by 9 for all non-negative n:

1. Check the base case, n = 1; 3 x 7 + 6 = 27, which is indeed divisible by 9.

2. First, we suppose x 7ⁿ + 6 is divisible by 9 for n ≤ k. i.e. 3 x 7^k + 6 = 9M for some integer M.

3. Then 3 x 7^k+1 + 6 = 7 x (3 x 7^k) + 6

4. This means 7 x (3 x 7^k) + 6 = 7(9M – 6)

5. Which means (3 x 7^k) + 6 = 9(7M – 4)

6. So 3 x 7^k+1 + 6 is also divisible by 9, which means 3 x 7ⁿ + 6 is divisible by 9 for all non-negative n.

Where is the first error?

The proof is correct.
Line (I)
Line (II)
Line (III)
Line (IV)
Line (V)
Line (VI)

The correct answer is B

This is a relatively simple question if you pay very close attention, as the first error is in line I and if you spot it, you don’t even need to check any other line due to the wording of the question. The question states “for non-negative n”, but the base case checked is n = 1. This is not the smallest non-negative number, 0 is. In fact, for n = 0, this conjecture is false, as 6 is not divisible by 9. The answer is therefore line (I).

That’s just a sample of what you should be looking for when you revise! If you need some ideas for your Paper 1 revision, check out our Definitive TMUA Paper 1 Guide for even more tips, tricks and practice questions.

You should now know what you’re going to need to become a TMUA master! We’ve learnt that it’s not all about pure mathematics in Paper 2 – you’re going to need to understand arguments and reasoning within both the questions and answer options presented. Your next step is to get out there and revise for the big day! Remember to check in with Exams.Ninja for even more TMUA Guides!

TMUA Results 2023 – The Definitive Guide to your TMUA Score

TMUA: The Definitive TMUA Starter Guide For 2024

TMUA Preparation: Your 6-Month TMUA Preparation Timeline

The Complete Guide to Algebra in the TMUA – Papers 1 & 2

TMUA Paper 2 – The Definitive Guide to Paper 2 of the TMUA

TMUA Paper 1 – Understanding the First Part of the TMUA

It’s your time to prepare for the TMUA, why not make the most of it with Exams.Ninja?

The TMUA is a tough exam to prepare for, but Exams.Ninja is here to help ease the burden of revision. With the TMUA Preparation Platform, you’ll have access to all these amazing features:

Training Temple- Exclusive tips, revision notes and 100+ expert tutorials will help you through the whole preparation process.

Practice Dojo- With over 500 practice questions, you’ll have more than enough to work through and become a maths expert! Each question also comes with a worked solution to make sure you have the knowledge to succeed.

Exam Arena- You can sit 5 full TMUA past papers in realistic exam conditions. You’ll be able to manage your stress so you don’t crack on the big day!

Start your TMUA prep today and maximise your chances of success!