TMUA Guides
The Complete Guide to Algebra in the TMUA - Papers 1 & 2
Written by: Matt Amalfitano-Stroud
Algebra is by far one of the broadest subjects within mathematics, and you’ll likely have been studying it for years at this point. Whether it comes as second nature for you or you’re struggling to keep track of all the rules and formulae, this guide will help you sharpen your skills within the topics you need to know for the TMUA. Let’s get started!
1/6
THE BASICS OF ALGEBRA AND THE TMUA
Here’s a quick rundown of the most basic information you’re going to need to know before you begin your preparation.

What is the TMUA?
The Test of Mathematics for University Admission (TMUA) is an examination sat by students applying to study Mathematics and maths-related subjects (such as Economics and Computer Sciences) at a selection of Universities around the UK. Among these unis are the University of Cambridge, London School of Economics and Imperial College London.
The TMUA is set out as a two paper exam that lasts 150 minutes, providing 75 minutes per paper. Each paper contains 20 multiple-choice questions (a total of 40 questions throughout the whole exam), covering Mathematical Application (Paper 1) and Mathematical Reasoning (Paper 2).
The TMUA is designed to test your mathematical knowledge at an advanced level, with questions related to principles and methods covered at A-levels (or equivalents). The TMUA Specification covers topics such as Geometry, Exponentials, Differentiation and, our topic for today, Algebra.
We also go into more depth about the TMUA specification in our guides for Paper 1 and Paper 2 of the TMUA! Check them out for more details on what to expect from each part of the test.
Basics of Algebra
In its most basic form, algebra is simply the process of assigning symbols to values and using set rules and formulae to manipulate said symbols. You’ll find simple algebra in many real-world applications, as it’s the most effective way to represent complex values and formulae in a readable format.
You’ll find symbols and algebraic principles in many other areas of maths, including Calculus and Graphs of Functions. But in its most elementary form, you can expect to see something like this:
x = 2y
y = 3
∴ x = 6
The algebra in the TMUA is going to be much more complex than this, so don’t think it’s going to be easy! Once you understand the basic function algebra, there are all sorts of rules and methods that you’ll need to learn, which is what we’re going to go through now! Let’s move on to the serious stuff!
Where should you start with your TMUA preparation?
You can cover your preparation from start to finish with the Exams.Ninja TMUA Preparation Platform! You’ll have all the resources you’ll need to get you ready for the big day!
2/6
THE FOUNDATIONS OF ALGEBRA
You should hopefully understand these principles already, but let’s refresh your memory to ensure that you understand these two major foundational elements of algebra.
Laws of Indices
The Laws of Indices (or Index Laws) are the first rules you’re going to need to know to be able to achieve anything in algebra. They define what can be done within an equation and how different values will react with each other. Considering m and n as any integers and rational numbers, the first three laws are as follows:
First Law – an x am = an + m
Second Law – (an)m = anm
Third Law – an/am = an – m
Following these, the additional laws of indices are as follows:
a0 = 1
a1 = a
a-1 = 1/a
a1/n = n√a
These are likely all identities you’ve seen before, but you’ve got to be confident enough to use them in unfamiliar circumstances. For example:
(xxx)x = x(xx)× x = x(xx +1)
Also note that surds can be written in these power formations as √x = x1/2. Therefore, if you see lots of expressions with powers and surds of x, then you should always be thinking “can I simplify down this expression before working with it further?”. For example, what if you were asked to find the derivative of the following function:
f(x) = (1 + x + (x2)2) / √x
You would simply first use the laws of indices to rewrite f in the simpler form – f(x) = x-1/2 + x 1/2 +x 7/2. You can then go on to differentiate using the standard differentiation rules.
Exams.Ninja Tip
You need to be able to apply all of these laws to any questions you will find in the TMUA. If you’re struggling to remember how each one functions, you’re going to need to apply some traditional revision techniques to keep the information stored in your mind.
Beyond regular refreshers and practice, you can maintain the knowledge subconsciously by leaving small posters and notes around your living space, preferably in areas you go to frequently. These rules are only small, so having constant reminders of them will allow you to maintain the information in no time!
Surds
Surds naturally follow from indices, as surds are just a different form of indices, so we can therefore use our indices laws as such. So, you just have to be comfortable to do everything above but instead of having x, there is now a number (we’ll use 2 as an example).
We also need to know how to rationalise the denominator of fractions of a particular form. To do this, we employ the trick of multiplying our fraction by 1 in a clever way, for example in the following:
1/ (1 + √2) = (1 – √2)/(1 + √2)(1- √2) = (1 – √2)/(1² – 2) = √2 -1
or
1/(√2 + √3) = (√2 – √3)/(√2+√3)(√2 – √3) = (√2 – √3)/(2 – 3) = √3 – √2
There may be some questions where you end up with an answer that you then (to map our answer to the multiple-choice option in the question) need to rationalise the denominator on, so you should be confident to be able to do this within a question.
Remember to keep these two principles with you as you proceed, they’re going to be relevant throughout the whole of your TMUA preparation. You can learn more about how to plan out your preparation effectively with our TMUA 6-Month Preparation Timeline!
3/6
QUADRATICS IN ALGEBRA
The quadratic formula is one of the most important formulas in algebra, so you’re going to need to know how it works and how you can use it to solve problems.
First things first, let’s clarify what we need to know about the quadratic equation:
ax² + bx + c = 0
Here, a, b, and c represent known values (a ≠ 0), while x is an unknown value.
A quadratic function is a function of the form f(x) = ax² + bx + c.
You should make yourself familiar with how to sketch quadratic graphs, such as the graph below which represents f(x) = 2x² + 3x + 4:
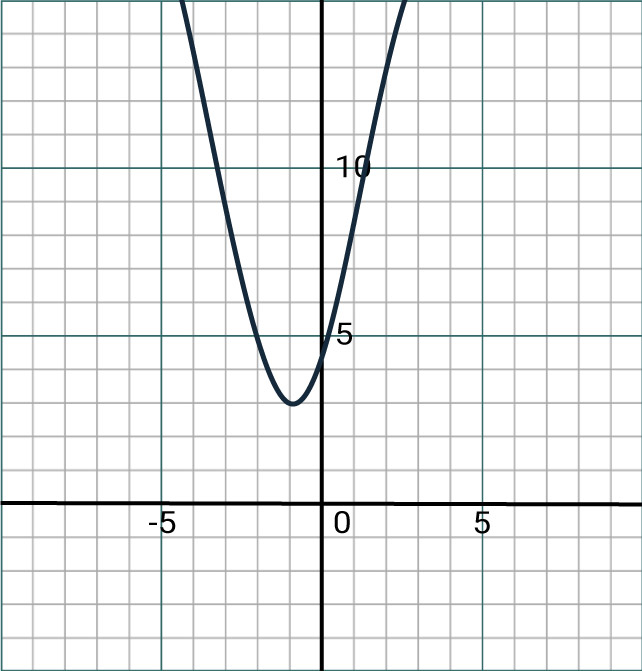
Quadratic graphs can be written in two different forms, each giving different pieces of helpful information:
f(x) = a(x – α)(x – β) = a(x + (b/a))2 + (c – (b2/a))
The former form gives us the roots of our quadratic fat α and β, and the latter gives us the vertex to our quadratic being at (-(b/a), c – (b2/a)).
When attempting a TMUA question on quadratics where you are considering a quadratic graph, you should ask yourself the question, “which features of the graph are important to this question?”. This will dictate which of the two forms will get you to your solution.
We can solve the quadratic equation ax² + bx + c = 0 by either factorising the quadratic directly, completing the square, or using the quadratic formula:
x = (-b ± √b2 – 4ac)/2a
[As an exercise you can derive the quadratic formula from completing the square.]
One thing to notice is that the quadratic has:
• 2 distinct real roots if b2 – 4ac > 0.
• 1 repeated root if b2 – 4ac = 0.
• No real roots if b2 – 4ac < 0.
This quantity (b2 – 4ac) is called the discriminant, and it is often easier to work with if we are discussing the “number of roots” of a quadratic over “finding the exact roots”. When attempting TMUA questions involving roots of a quadratic, you should try and distinguish whether you are wanting to find out information about the number of real roots or the exact values of the roots, as this will most likely dictate your method.
Note also that completing the square on the quadratic can often be helpful if you’re trying to show that a function is positive or negative everywhere.
Sometimes complicated equations can be solved by considering a substitution that transforms the equation to something easier to solve, such as a quadratic. Consider the example below:
4x – 3 x 2x + 1/2 + 4 = 0
We substitute y = 2x to give:
y² – (3√2y) + 4 = 0
(y – √2)(y – 2√2) = 0
y = √2 = 21/2 or y = 2√2 = 23/2
x = 1/2 or x = 3/2
You will also be expected to solve quadratic inequalities. To solve quadratic inequalities we use the following method:
Suppose we wish to solve the inequality ax2 + bx + c > 0.
- First, solve the equation we would get if we changed the inequality to an equals sign: ax2 + bx + c = 0.
- Sketch the graph of y = ax2 + bx + c, making sure to label the x-axis intercepts.
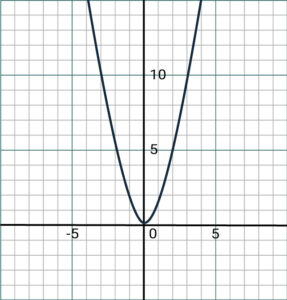
3. Read off from the graph the values of x for which the graph lies above the x-axis (the values of x for which y > 0.
Exams.Ninja Tip
Often a TMUA question isn’t going to get you to just simply use one of these methods, but rather use these methods as building blocks in a larger question. Therefore you should feel comfortable doing these building blocks in turn.
Check out our practice TMUA questions to give it a go, or check out the worked solution if you’re not sure where to start.
4/6
ALGEBRAIC MANIPULATION OF POLYNOMIALS
Polynomials are extremely common in algebra, especially at an advanced level. Therefore, you’re going to need to be able to manipulate them in a variety of ways in order to solve problems. Let’s have a look at how it’s done!
To start with, let’s remind ourselves of what exactly a polynomial is. They’re defined as a mathematical expression that involves a sum of powers in one or more variables multiplied by coefficients.
The components of a polynomial are referred to as monomials, which are simply a single term. There are actually several names for polynomials of different sizes:
Monomial – A polynomial with one term – 2x3
Binomial – A polynomial with exactly two terms – 2x3 + 5x
Trinomial – A polynomial with exactly three terms – 2x3 + 5x + 6
An expression with any more than 3 terms is simply referred to as a polynomial.
Bare in mind that a monomial can only contain whole numbers as exponents. As an example, 2x-3 is not a monomial as the exponent has a value less than zero.
When given a polynomial, we should always be on the lookout as to whether we can factorise it. This is because sometimes we can really simplify our working by getting our polynomials in their simplest factored form. For example:
(x2 + x -2)/(x – 1) = ((x – 1)(x + 2))/(x – 1) = x + 2
We should also feel comfortable not only working with the factorisation of polynomials but also the division of polynomials. This is closely related to the Factor and Remainder Theorem, which are outlined below:
Factor Theorem: If f(x) is a polynomial and f(a) = 0 then x – a is a factor of f(x).
This Factor Theorem is therefore able to be used to verify a factor of a polynomial and is the first step in factorising a polynomial fully.
A generalisation of the Factor Theorem is the Remainder Theorem.
Remainder Theorem: If f(x) is a polynomial then f(a) is the remainder obtained when we divide f(x) by x – a.
Let’s look at an example that winds these theorems with forming algebraic equations:
Manipulation of Polynomials Example Question
When (3x2 + 8x – 3) is multiplied by (px – 1) and the resulting product is divided by (x + 1), the remainder is 24. What is the value of p?
We first need to translate the wordy nature of the question into a firm mathematical statement:
f(x) = (3x2 + 8x – 3)(px – 1) divided by (x + 1) gives the remainder 24.
Then using the remainder theorem we get the following:
f (-1) = 24
(3 – 8 – 3)(-p – 1) = 24
8(p + 1) = 24
p + 1 = 3
Which gives us our answer:
p = 2
Lastly, you’re going to need to know the formula for Binomial Theorem. You’ll need this for when you need to expand an expression in the form of (a + b)n. Remember, the larger the power, the more difficult it will be to expand the expression directly.
Binomial Theorem
(x + a)n = n∑k = 0 (n k)xkan – k
There are plenty more TMUA resources waiting for you now!
With the Exams.Ninja TMUA Preparation Platform, you’ll have instant access to over 100 expert tutorials, 500+ practice questions and 5 full mock papers. All available from the comfort of your home!
5/6
SIMULTANEOUS EQUATIONS AND FURTHER INEQUALITIES
These two areas of algebra are likely to show up in the TMUA, so let’s take a look at how we can tackle each one!

Simultaneous Equations
When working with simultaneous equations we have one key method and aim – trying to reduce a problem involving variables x and y into a problem involving just one of x or y that we can solve. We do this by the substitution method for simultaneous equations:
- Write y in terms of x using one of the two equations given.
- Substitute this formula for y in terms of x into the second equation.
- Solve the resulting equation for x.
- Use the formula for y found in part 1 to find y.
To put this method into action consider the following example:
Suppose we wish to solve this set of simultaneous equations:
x4 + y2 + 2x = 1, x + y = 1
Using our step by step method, we choose to rewrite our second equation as:
y = 1 – x
Substituting this into our first equation gives us an equation entirely in x.
x4 + (1 + x)² + 2x = 3
x4 + 1 – 2x + x² + 2x = 3
x4 + x² – 2 = 0
We at this stage can spot we have a hidden quadratic, so taking z = x² we have:
z² + z – 2 = 0
(z + 2)(z – 1) = 0
z = -2 or z = 1
x² = -2 or x² = 1
But then x² ≥ 0 so the first root is not possible, so we have:
x² = 1
x = 1 or x = -1
Substituting these values of x back into our formula for y = 1 – x we get:
(x,y) = (1,0) or (-1,2)
Further Inequalities
As a word of warning, make sure to never divide an inequality by something that is either negative or could be negative without changing the sign of the inequality. Often you get caught out when multiplying or dividing by an expression in x. For example, we cannot say:
(x + 1)/x > 0 ⇒ x + 1 > 0
So how do we solve this inequality above? Much like as we saw for quadratic inequalities, drawing a graph with any inequality can help paint a clearer picture of what is going on. So, for example, a sketch of the curve y = (x + 1)/x shows us in fact that:
(x + 1)/x > 0 ⇒ x < -1 or x > 0
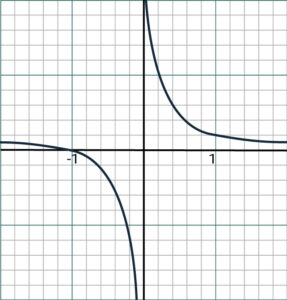
Try out the practice questions below to hone your skills on some real TMUA style questions!
6/6
TMUA ALGEBRA PRACTICE QUESTIONS
Now that we’ve gone through the algebraic techniques you’ll need to know for the TMUA, it’s time to start practising. Try out these exam-style questions and check your technique with the worked solutions.
TMUA Algebra Paper 1 Question 1
In which of the following ranges is (x2 – 1)(x + 2)(x + 4) > 0?
A) -2 < x < 1
B) -1 < x < 2
C) -2 < x < -1
D) x ≥ 1
E) x < -3
The correct answer is C.
We may factorise the function as (x – 1)(x + 1)(x + 2)(x +4), which allows us to graph it.
TMUA Algebra Paper 1 Question 2
Given f(x) = (9x2 + 12 + (4/x2))1/2 and dnf/dxn(2) = -3/4, find n.
A) 1
B) 2
C) 3
D) 4
E) 5
The correct answer is C.
Note that the inside of the bracket is a perfect square and is simply (3x + (2/x))2.
Therefore, f(x) = 3x + (2/x), f’(x) = 3 – 2/x2, f”(x) = 4/x3 , f”’(x) = – 12/x4 and so f”’(2) = -3/4.
TMUA Algebra Paper 1 Question 3
Find the coefficient of x³ in the binomial expansion of y = (2x -1)9.
A) 8
B) -8
C) 72
D) -72
E) 112
F) -112
G) 672
H) -672
The correct answer is G.
The expansion coefficients for n = 9 are unlikely to be known, so instead the formula n!/(r!(n – r)!) must be used.
Expansion coefficients = 1, 9, 36, 84, 126, 126, 84, 36, 9, 1
Expansion = (2x)9 + 9(2x)8(-1) + 36(2x)7(-1)² + 84(2x)6(-1)²…..
The coefficient for x³ will be (84)(2)³(-1)6 = 672
TMUA Algebra Paper 1 Question 4
4x² – 7x + 1 is multiplied by 2x – q to form f(x). f(x) divided by (x + 2) is -31².
What is q?
A) 27
B) 35
C) There is no such q
D) – 27
E) -35
F) 21/2
The correct answer is A.
We first determine what f(x) is:
(4x² – 7x + 1)(2x – q) = 8x³ – 14x² +2x – 4qx² + 7qx – q.
f(x) divided by (x +2) is the same as f(-2) = 8 x -8 – (14 + 4q) x 4 + (2 + 7q) x (-2) – q = -31q -124 = -31².
This gives us q + 4 = 31, so q = 27.
TMUA Algebra Paper 2 Question 1
The polynomial x³ + (a – 3)x² + (b – 3a)x – 3b has exactly two roots. Which of the following is true?
A) a² – 4b = 0 is necessary.
B) a² – 4b = 0 is sufficient.
C) a² – 4b = 0 is necessary and sufficient.
D) b² – 4a = 0 is necessary.
E) None of the above.
The correct answer is A.
Note that 3 is an obvious root:(x – 3)(x² + ax + b) = x³ + (a – 3)x² + (b – 3a)x – 3b. So now we require x² + ax + b = 0 to have one solution, but note it can’t be 3. The discriminant a² – 4b =0 is this a necessary condition but not sufficient. We would require additionally the condition 9 + 3a + b ≠ 0.
TMUA Algebra Paper 2 Question 2
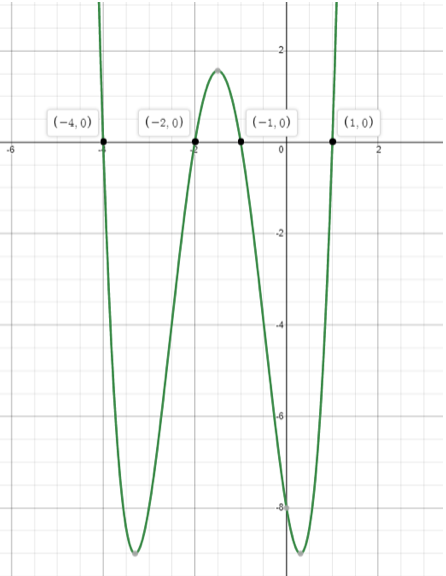
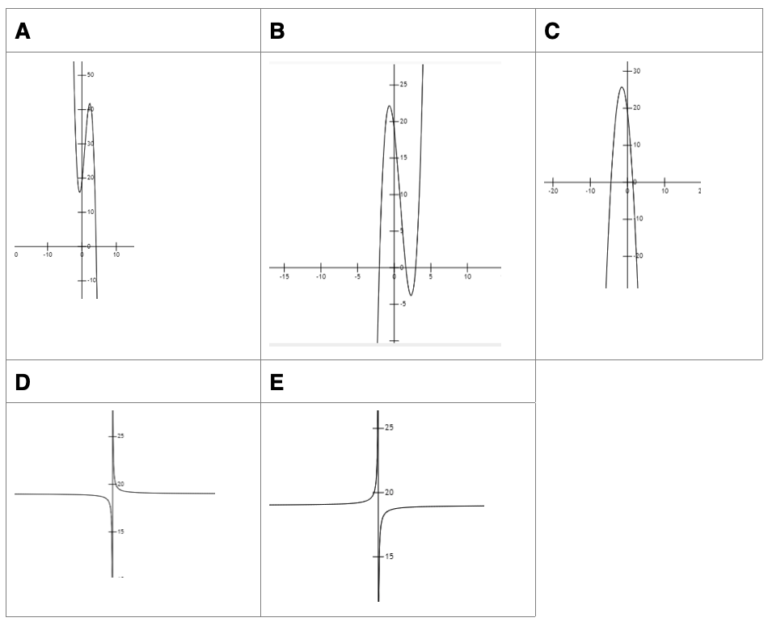
Which of the following graphs shows the equation y = 2x³ – 5x² – 9x +19?
The correct answer is B.
- y intercept is at 19
- the gradient is positive at first, so positive x3
- A is a negative cubic graph, C is a quadratic, D and E are reciprocal graphs
TMUA Algebra Paper 2 Question 3
Find the sum of the values of a such that the quartic equation x4 – x3 – x2/2 = a has an odd number of solutions.
A) 3/4
B) -1/2
C) There are no values of a.
D) – 134/256
E) 117/256
F) – 117/256
The correct answer is D.
Quartic equations only have an odd number of solutions if there is a stationary point on the line y = 0. So, we differentiate to find x(4x³ – 3x – 1). Setting this equal to 0, we find stationary points at x = 0, 1, – 1/4.
Then, we substitute into the original equation and find we have a = 0, – 1/2 and – 3/28. This means these are the values of a for which the stationary point is a solution, and thus there is an odd number. i.e. the sum of values is- 131/28.
TMUA Algebra Paper 2 Question 4
Consider this student’s attempt at finding the solutions to √x + 3 = 3x – 1:
- x + 3 = (3x – 1)²
- x + 3 = 9x² – 6x + 1
- 0 = 9x² – 7x – 2
- 0 = (x -1)(9x + 2)
- So x = 1 and – 2/9
Is this correct?
A) Both answers are correct.
B) Only one is right and it’s due to an error in line (I).
C) Only one is right and it’s due to an error in lines (II) and (III).
D) Only one is right and it’s due to an error in line (IV).
E) Neither is right and it’s due to an error in line (I).
F) Neither is right and it’s due to an error in lines (II) and (III).
G) Neither is right and it’s due to an error in line (IV).
The correct answer is B.
It is easy to check which of the roots are right by substituting into the original equation. We see that x = 1 is fine, but if x = – 2/9, the right-hand side is less than 0, but the √x symbol denotes taking the positive root. Thus, only x = 1is correct. The error occurred in line (I) due to assuming no roots were generated from squaring both sides. This is what created the 2nd root.
These questions represent most of what you will find in the TMUA in terms of algebra questions. So now it’s time to leap headfirst into your revision. You’ll need to be answering practice questions very regularly in order to ensure you have confidence when it comes to the real test.
As well as our own TMUA Preparation Platform, which contains over 500 practice questions, you’ll also want to keep an eye on the Exams.Ninja website for more guides and practice questions coming soon.
Trying to work out the perfect TMUA preparation plan? Exams.Ninja is here to help!
Finding good revision resources can be tough, but with the TMUA Preparation Platform, you’ll have everything you need at the click of a button! Our incredible features include:
Training Temple- You’ll be able to access over 100 tutorials created by TMUA experts, along with tons of extra revision notes and tips.
Practice Dojo- With over 500 practice questions from both papers of the exam, you’ll have enough to keep you busy right up until the big day!
Exam Arena- Ready for a real challenge? Take on the 5 TMUA past papers and see what it’s like to sit the real exam. You’ll see how you work under pressure and what you would’ve scored in the actual exam.
So why wait, get started with your TMUA preparation today!