YOUR ULTIMATE GUIDE
The Definitive Starter Guide To The TMUA (2024)
Written by: Matt Amalfitano-Stroud
The TMUA is one of the major hurdles in between you and getting your dream place at university. This guide is the first stepping stone on your journey to beating the exam, as you will learn everything you need to know about its format, the two papers and the questions you’ll find on exam day. Let’s get started!
1/3
TMUA BASICS: EVERYTHING YOU NEED TO KNOW
The first thing we need to take a look at is everything surrounding the TMUA. Let’s go over how you register, how it’s scored, what you need to bring and much, much more.


What is the TMUA?
The Test of Mathematics for University Admission (TMUA) is a pretty self-explanatory title. But just to clarify, it’s a 150 minute long admissions test used by a variety of universities primarily for their Mathematics courses.
The key thing to understand about the TMUA is that, in some cases, it is a non-compulsory exam. Many of the universities that use the TMUA give applicant’s the opportunity to apply for their courses without submitting TMUA results. In some cases, this may be because they accept multiple admissions exams, while others simply do not make it a requirement.
However, it is highly recommended that sit the exam and aim to score highly, as, in some cases such as Durham University and Warwick University, achieving a certain score will likely get you an offer or even a reduced offer. Other’s, such as LSE, have clearly stated in the past that the TMUA makes you a more competitive candidate.
In recent years, predicted grades have become less relevant within university admissions, meaning the TMUA is much more important to making your application stand out (although the other parts of your application will still need to be strong).
The key exceptions to this are the University of Cambridge and Imperial College London, who require all applicants (excluding mature students) to sit the TMUA for various courses, including Computer Sciences and Economics courses.
TMUA 2024 Updates
As of 2024, the TMUA is now being run by University Admissions Tests UK (UAT), a new sub-brand of the testing organisation Pearson VUE. This has affected multiple things, including the programme on which the test is taken on, the location of testing and the dates that the test is sat on. All of the information featured below is updated for the 2024 admissions cycle.
What is the Structure of the TMUA?
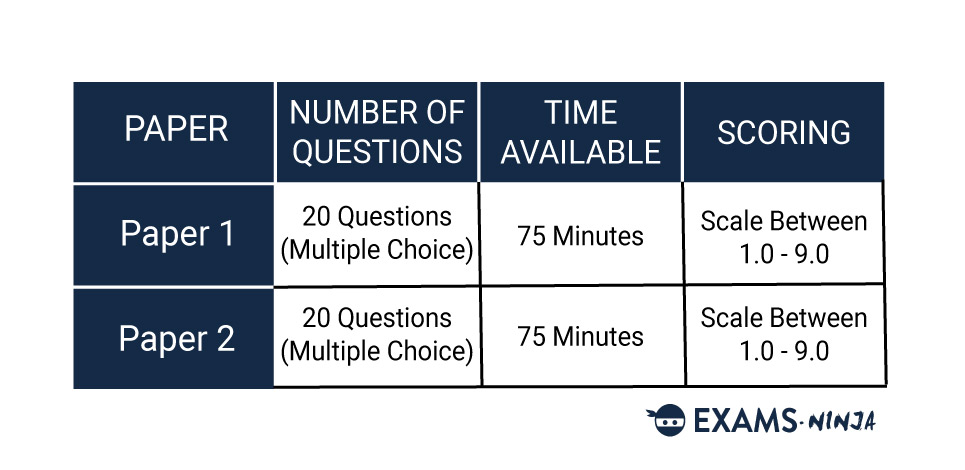
The TMUA is made up of two separate papers consisting of 20 multiple-choice questions each. You are given 75 minutes to complete each paper. The questions on each paper are fairly different to each other:
Paper 1 focuses on mathematics in its purest form. These questions are laid out simply and will see you solving the problem that is presented to you.
Paper 2 focuses more on mathematical reasoning rather than pure knowledge. Many of the questions presented will require more than just solving a problem but to logically assess a problem or another person’s work using various techniques. Mathematical knowledge will still be essential here, but the question will be less about the solution and more about the context of the question or solution given.
This table summarises the TMUA Structure:
TMUA Structure
Why is the TMUA used?
As previously stated, the TMUA is primarily used as a tool for assess applicant’s mathematic abilities, both in terms of pure maths and logical thinking.
As a non-essential exam for the most part, it can be assumed that admissions teams will look more highly upon applicants who have sat the exam and will generally be more likely to give an offer if a high TMUA score has been achieved.
Many of the courses that accept the TMUA do not require applicants to interview, meaning this exam will be their primary way of understanding your abilities as an academic. This will typically be considered alongside your personal statement, which will give them an idea of your attitude and personality.
How much does the TMUA cost?
In order to sit the TMUA, applicants will have to pay a fee of either:
TMUA UK/EU Fee
£75
TMUA International Fee
£130
Bursary vouchers are available to cover these costs, the dates to apply for these are from June 3rd 2024 to September 16th 2024.
When and where is the TMUA sat?
The TMUA will be sat in two sessions of two days across 2025 and 2026. The First testing dates are the 13th and 15th October 2025 and the second are the 8th and 9th January 2026. Cambridge applicants can only sit the TMUA during the first testing period, but other applicants can also sit their test during the second period.
The TMUA will need to be sat at one of over 5,500 testing centres across 160 countries. You will be able to locate your nearest centre when registering to sit the test.
How to Register for the TMUA
Registration for the TMUA begins August 1st and is being organised by Pearson VUE, who run a wide variety of tests in the UK. You will need to register via a Pearson VUE account, which can be created on their website. You will need to provide various personal details to do so, including your UCAS number. The deadline for registration varies depending on when you sit the test, with the first-period deadline being September 16th 2024 and the second deadline being December 9th 2024. Access arrangements will also need to be highlighted during this process.
Who has to sit the TMUA?
The TMUA is accepted by 6 universities. As previously stated, the TMUA is required by Cambridge for their Computer Sciences and Economics courses. Other universities in this list either require the TMUA to be sat or will accept results to support your application:
TMUA Universities
- Computing (BSc)
- Economics, Finance and Data Science (BSc)
- Joint Mathematics and Computer Science (BEng/MEng)
- G100 Mathematics (3-year course)
- G103 Mathematics (4-year course)
- G125 Mathematics (Pure Mathematics)
- G104 Mathematics with a Year Abroad
-
G1F3 Mathematics with
Applied Mathematics/Mathematical Physics -
G102 Mathematics with Mathematical
Computation - G1G3 Mathematics with Statistics
- G1GH Mathematics with Statistics for Finance
Mandatory
Non-Mandatory
Mandatory
Mandatory
Non-Mandatory
Key TMUA Dates
As we’ve just seen, the TMUA will be sat on multiple days across multiple months, but there are various other important dates to keep in mind, so be sure to remember these:
| Applicants Deadlines 2023 | |
|---|---|
| Registration Opens (October Testing) | TBC |
| Registration Closes (October Testing) | TBC |
| TMUA Testing (October) | 13th – 14th October 2025 |
| Registration Opens (January Testing) | TBC |
| Registration Closes (January Testing) | TBC |
| TMUA Testing (January) | 8th – 9th January 2026 |
| TMUA Results Released | TBC |
But when should you start preparing? We would recommend starting six-months in advance! You can see how we suggest you use your time with our TMUA Preparation Timeline.
What do I Need for the TMUA?
The TMUA is a computer-based assessment, meaning all answers are selected through a specific testing programme. However, you will be given paper for working out, so on the day you’re going to need take a soft (HB) pencil with you. Calculators are not permitted in the TMUA, along with any other supporting materials.
However, taking a watch with you is always a good idea. Try to bring one that can show you the time in seconds, as this will allow you to have a much more accurate idea of the time you’re spending on a question.
You will also be required to bring a form of ID to the testing centre, or else you will not be admitted into the testing centre.
How Hard is the TMUA?
At first glance, the TMUA may seem like a fairly easy test. You’re given two and a half hours to answer 40 multiple choice questions, all of which are focused on mathematics. If you have effectively prepared and are confident with you mathematical abilities, then the TMUA should be more than possible to succeed in.
That’s not to say that the TMUA is easy though, as these questions will be testing you on advanced level maths. You’re going to need to be confident with maths up to A-Level difficulty (or equivalent), so some of the topics covered will be fairly new to you. Everything covered will be in your school curriculum however.
Be aware that Paper 2 may trip you up if you haven’t properly practiced it. These questions rely more on mathematical reasoning than just pure mathematics, so the logic-based questions may catch you off guard.
Can I resit the TMUA?
Students cannot attempt the test twice during the same admissions cycle. If you apply again in another admissions cycle, you must take the test again.
Some universities do accept alternate admissions tests, including the MAT and STEP, so be sure to take one of these exams if you’re unhappy with your TMUA score.
How is the TMUA scored?
In the TMUA, each question is worth one mark. Your raw marks out of 40 will be how many questions you got correct. There is no negative marking so incorrect answers will not deduct marks from your total.
For your final result, your raw marks are converted and placed into a scale from 1.0 to 9.0. These are the scores that your prospective universities will see. Below you will find the Score Conversion Tables for both papers of the TMUA, as well as the overall conversion out of 40:
TMUA Paper 1 Score Conversion Chart
| Paper 1 Raw Score | Paper 1 Grade |
|---|---|
| 20 | 9.0 |
| 19 | 9.0 |
| 18 | 8.3 |
| 17 | 7.9 |
| 16 | 7.6 |
| 15 | 7.3 |
| 14 | 7.0 |
| 13 | 6.8 |
| 12 | 6.6 |
| 11 | 6.1 |
| 10 | 5.6 |
| 9 | 5.0 |
| 8 | 4.5 |
| 7 | 3.9 |
| 6 | 3.3 |
| 5 | 2.6 |
| 4 | 1.9 |
| 3 | 1.0 |
| 2 | 1.0 |
| 1 | 1.0 |
| 0 | 1.0 |
TMUA Paper 2 Score Conversion Chart
| Paper 2 Raw Score | Paper 2 Grade |
|---|---|
| 20 | 9.0 |
| 19 | 9.0 |
| 18 | 8.3 |
| 17 | 7.8 |
| 16 | 7.5 |
| 15 | 7.2 |
| 14 | 6.9 |
| 13 | 6.7 |
| 12 | 6.3 |
| 11 | 5.7 |
| 10 | 5.1 |
| 9 | 4.5 |
| 8 | 3.9 |
| 7 | 3.3 |
| 6 | 2.7 |
| 5 | 1.9 |
| 4 | 1.1 |
| 3 | 1.0 |
| 2 | 1.0 |
| 1 | 1.0 |
| 0 | 1.0 |
TMUA Overall Score Conversion Chart
| OVERALL RAW SCORE | 40 | 39 | 38 | 37 | 36 | 35 | 34 | 33 | 32 | 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OVERALL GRADE | 9.0 | 9.0 | 9.0 | 8.6 | 8.3 | 8.1 | 7.9 | 7.7 | 7.5 | 7.4 | 7.2 | 7.1 | 7.0 | 6.8 | 6.7 | 6.6 | 6.5 | 6.2 | 5.9 | 5.6 | 5.4 | 5.1 | 4.8 | 4.5 | 4.2 | 3.9 | 3.6 | 3.3 | 3.0 | 2.6 | 2.3 | 1.9 | 1.5 | 1.1 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
How do the universities get my results?
As the TMUA is non-compulsory for most universities, your results will not be automatically sent to them. Instead, you will need to submit them yourself once you have received them on November 29th. Here is the process of doing so:
- At the end of your test, you will receive a Confidential Results Information sheet. This contains login details for you account on Metritests. This is where you will be able to access your TMUA results when they are published.
- Under the TMUA test option, you will need click “Share Results” in order to begin the process.
- You will then need to select the universities you wish to send the results to, as well as the degree. Once you have saved this option on the site, the results will be immediately available for the universities to see.
Please note that sending the results is not a requirement after you have completed the TMUA. If, for whatever reason, you decide you don’t want your chosen universities to see your results, then simply do not complete the process outlined. The rest of your application will not be affected by this.
If you’re applying to the University of Cambridge, your results will be automatically sent to the university. There is no option to withhold your results. We have a full guide about TMUA Scoring and Results that will show you what your score means and how it is used.
It’s never too early to begin your TMUA preparation, so start now with TMUA.Ninja!
With our TMUA Preparation Platform, you can get access to 100’s of practice questions for everything covered in the TMUA. Sign up now for free to begin your TMUA prep.
2/3
TMUA PAPER 1
With the basics out of the way, let’s take look at the first paper in the TMUA, which is all about pure mathematics.
Paper 1 of the TMUA is (obviously) is the first half of the TMUA. Here, you will find 20 multiple-choice questions testing your pure mathematics skills in a variety of disciplines. While the questions are relatively straight-forward format-wise, they are far from easy!
When we say that they’re straight-forward, we mean that you’re going to solving mathematical problems and not too much else.You’re goal here is to find the solution to the mathematical problem presented to you, which is what you’d typically expect from a maths exam at this level.
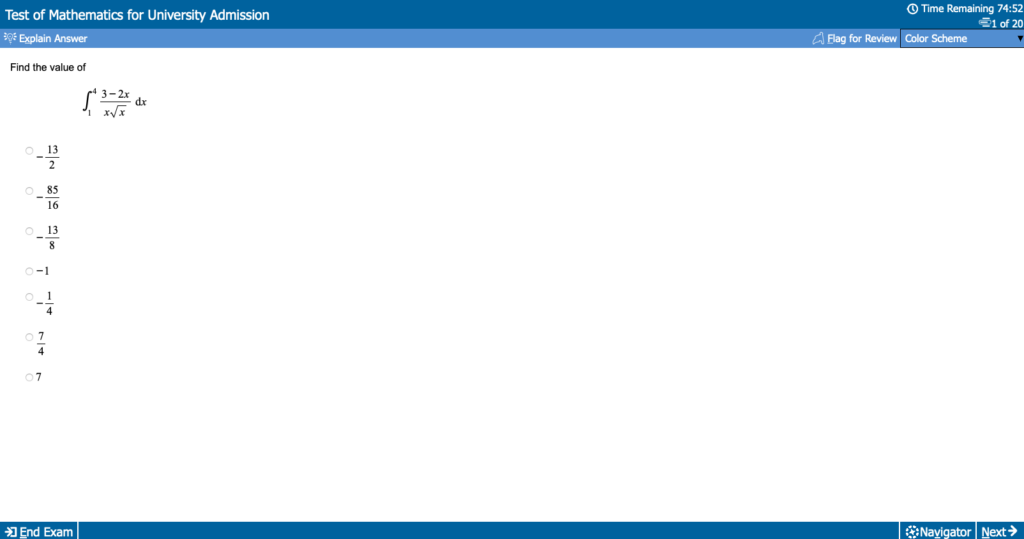
You can see below exactly what to expect from a page on the TMUA:
TMUA Paper 1 Example Page
Each page contains just one question, with the buttons to go back or forwards being at the bottom of the page. All of your answer options will be presented under the question, you will have to select the option you feel is correct by clicking the circle (this can be changed at any time, even if you move to a different question. You can flag any question to highlight that you wish to go back to it before the end of the test (this does not affect your marks).
You will have access to paper to do rough working out for each question, this will not be marked or considered in any way.
There is a review screen that can be viewed once you’ve gotten to then end of the 20 questions. This screen will give you a chance to see if any questions have been missed/flagged and to go back to them.
TMUA Paper 1 Specification
Next up, it’s time to look at the exam specification for the TMUA. This is the official list of every topic that will potentially appear in the TMUA. The specification is split into two sections, Section 1 and Section 2. Section 1 covers all of the pure mathematical knowledge that you’re going to need to know when sitting the TMUA and is required for both papers.
Section 1 is further spilt into two ‘Parts’, Part 1 and Part 2. Essentially, Part 1 covers Advanced Maths while Part 2 covers Standard Maths (which feels like the wrong order!). It feels strange to begin with the advanced knowledge required for the exam, so we’ll go out of the order of the specification and begin with Part 2:
TMUA Specification: Section 1, Part 2
- Use the four functions on whole numbers, integers, fractions, decimals and numbers in index form.
- Use terms relating to factors and squares.
- Use index laws.
- Understand equivalent fractions.
- Convert between fractions, percentages and decimals.
- Understand direct and indirect proportion.
- Use ratio notation.
- Use surds and Pi in exact calculations.
- Understand number operations and their uses.
- Calculate upper and lower bounds to contextual problems.
- Know and use approximation methods to a specified degree of accuracy.
- Be able to use standard units for length, mass, money, time and more.
- Be able to use compound units including density, pressure, rates of pay, speed and unit pricing, plus decimal quantities where applicable.
- Convert between related units and compound units in numerical and algebraic contexts.
- Distinguish the roles of different letter symbols.
- Manipulate algebraic terms.
- Use index laws in relation to algebra.
- Know and use (ab)c = abc.
- Set up and solve linear equations, including simultaneous equations.
- Factorise quadratics.
- Simplify rational expressions
- Set up and solve quadratic equations.
- Derive formulae, substitute into a formula and change the subject of a formula.
- Solve linear inequalities.
- Generate terms of a sequence and describe the nth term with linear expressions.
- Use Cartesian coordinates in 4 quadrants.
- Know and understand the equations of straight lines, including y = mx + c.
- Solve simultaneous equations with a linear and a quadratic.
- Recognise and interpret various graphs, including quadratic functions and cubic functions.
- Construct linear functions from actual problems, including graphs.
- Know and use properties of angles at various points.
- Understand and use various angle properties.
- Calculate and use the fumes of angles in polygons.
- Recognise and use reflectional and rotational symmetry in 2D shapes.
- Understand congruence and similarity.
- Use Pythagoras theorem in 2D and 3D.
- Understand on create geometrical proofs, include the use of circle theorems.
- Represent 3D shapes in 2D.
- Describe and transform 2D shapes with various techniques.
- Understand and use the standard trigonometric ratios of sin, cos and tan.
- Understand and be able to use scale factors, scale diagrams and maps, as well as ratio notation.
- Express quantities as fractions of another, if a fraction is less than or greater than 1.
- Divide 2 quantities into multiple parts as a ratio of part:part, as well as express the division of two parts as a ratio.
- Use ratios in realistic contexts, including problems that involve comparison, concentrations, conversion, mixing and scaling.
- Understand and be able to use proportion, such as relating ratios to fractions or linear functions. This also includes direct and inverse proportional including algebraic representations.
- Be able to work with fractions in ratio problems.
- Work with percentages, including expression of quantities as percentages, comparing two quantities through percentages, working with percentages over 100% and interpreting percentages and percentage changes as fractions or decimals.
- Complete problems that include percentage changes such as increases/decreases and simple interest calculations.
- Be able to set up and interpret equations to solve problems involving direct and indirect proportion, as well as understanding graphs that illustrate these proportions.
- Know and understand that x is inversely proportional to y, the equivalent to x is proportional to 1/y.
- Compare areas, lengths and volumes with ratio notation, and make links to similarity and scale factors.
- Know and understand growth and decay problems that include compound interest, plus work with general iterative processes.
- Identify potential sources of bias.
- Identify flaws in various data collection methods.
- Group and understand discrete and continuous data.
- Extract data from tables and lists.
- Design and use two-way tables.
- Interpret various forms of chart, including bar charts and line graphs.
- Interpret cumulative frequency in various forms, including tables and graphs.
- Calculate and interpret averages in data, including mean, median and mode.
- Calculate average rates in combines samples/events.
- Interpret scatter diagrams and identify correlations with line of best fit.
- Make comparisons between data sets with statistical measures and graphical representations.
- Understand and use the vocabulary of probability and the probability scale.
- Understand and use the estimates and measures of probability, including relative frequency and theoretical models.
- List outcomes fro single and combine events.
- Identify different mutually exclusive outcomes.
- Construct and use Venn diagrams to solve union and intersection categorisation problems.
- Know when to add or multiple two probabilities.
- Understand the use of tree diagrams to represent outcomes of combined events.
- Compare experimental and theoretical probabilities.
- Understand repeated experiments with different outcomes.
None of this should be particularly tricky for you, so let’s move straight on to the more advanced stuff; Part 1:
TMUA Specification: Section 1, Part 1
- Know and use the laws of indices.
- Know and use the manipulation of surds.
- Understand and use quadratic functions, including graphs, use of discriminant and completing the square.
- Know how to sovle simultaneous equations via substitution.
- Know how to solve linear and quadratic inequalities.
- Know and understand the manipulation of polynomials e.g. expanding brackets, factorising.
- Know and use Factor Theorem and Remainder Theorem.
You can check out out TMUA Algebra Guide to learn even more about what you need to revise.
- Know and understand Arithmetic series and Geometric Series.
- Understand summing to a finite and infinite geometric series.
- Know and use binomial expansions.
- Know and use factorials.
- Know and use equations for circles.
- Know and use equations for straight lines.
- Know and understand circle properties.
- Know the solution of trigonometric identities.
- Know and understand the values of sin, cost, tan for 0, 30, 45, 60 and 90 degrees.
- Understand and interpret Sine, Cosine, Tangent graphs, symmetries, periodicities.
- Know and understand the graph of y = ax series.
- Solve equations of the form ax = b.
- Understand and use the Law of Logarithms:
- ab = c <-> b = logac
- logax + logay = loga(xy)
- logax – logay = loga(x/y)
- k logax = loga(xk)
- loga 1/x = – logax
- logaa = 1
- Know and understand first order and second order derivatives.
- Know and use differentiation of functions like y = xn.
- Have familiarity with notation.
- Know and use definite and indefinite integrals for y = xn
- Solve Differential Equations in the form: dy/dx = f(x).
- Understand the Fundamental Theorem of Calculus and its application.
- Combining integrals with either equal or contiguous ranges
- Solve differential equations in the form of dy/dx = f(x).
- Know and use the trapezium rule.
- Understand sketching of common functions including lines, quadratics, cubics, trigonometric functions, logarithmic functions and exponential functions.
- Know and use the graph of series y = ax.
- Know and use the manipulation of functions with simple transformations.
- Use geometric interpretation of algebraic solutions of equations.
That’s a fair amount to take in, but none of this should be new to you. Remember that the TMUA deals with content knowledge up to A-Level difficulty, so everything in the specification should be covered within your school’s curriculum. Just bear in mind the order your school teaches in may mean some topics are not covered before you sit the exam in October. If this is the case, you will need skip forward a bit and teach the topic to yourself, although asking your teacher for help is always a good idea!
If you want to learn more about this part of the exam, want to try out some practice questions or are just looking for some preparation tips, be sure to check out our TMUA Paper 1 Guide.
TMUA Paper 1 Practice Questions
With all that in mind, it’s time to take a look at some TMUA Practice Questions to put your knowledge to the test:
TMUA Paper 1 Practice Question 1
Given that, in the expansion of (3x + b)7, the coefficient of x4 is the same as the coefficient of x² in (3b + x)4, find the positive constant b.
A) 2/105
B) 105/2
C) 107/3
D) 3/107
E) 109/4
The correct answer is A.
In the first expansion, the coefficient of x4 is given by (74)34b3 = 2835b³ and in the second, the coefficient of x² is (42)(3b)2 = 54b², and equating, we see that b = 54/2835 = 2/105.
TMUA Paper 1 Practice Question 2
Find the distance between the intersection points of y = |x – 4| and y = 5 – |x – 1|.
A) There are no intersections
B) 4
C) √34
D) 5
E) 3
F) √41
The correct answer is C.
Knowing that the highest point of y = 5 – |x – 1| will be at x = 1 tells you that point is at (1,5), which is above the line y = |x – 4| as it is at (1,3) there. This tells you there are two intersection points, with a quick sketch.
While this may or may not be to scale, it doesn’t matter; we can see from the sketch that there is one intersection when both are in their first half, and one in their second half, whether the apex or base of either two graphs should be closer or further apart is irrelevant. Thus, we solve 5 – (x -1) = x – 4 (gives x =5) and 5 + x – 1 = 4 – x (gives x = 0).
These points are (5,1) and (0,4) respectively and using Pythagoras’ Theorem tells us their distance is √(5 – 0)² + (1 – 4)² = √25 + 9 = √34.
TMUA Paper 1 Practice Question 3
Every day, a man decides whether to walk his dog with probability 1/3 that he does take it for a walk, independently of choices made on other days. After 4 days, what is the probability that he walked his dog at least once every 2 days?
A) 1/27
B) 7/27
C) 8/27
D) 11/27
E) 1/9
F) 1/3
The correct answer is B.
For the man to walk his dog “at least once every two days”, we know he never had two consecutive days which he did not walk the dog. So, representing going for a walk as W and not going as N, the possible ways he spent his 4 days are WWWW, WWWN, WWNW, WNWW, NWWW, NWNW, NWWNWNWN. These are not all equally likely as each W has 1/3 chance of appearing, and each N has a 2/3 chance. Thus, the probability that each set of 4 days occurred is 1/81, 2/81, 2/81, 2/81, 2/81, 4/81, 4/81, 4/81.
As we only want to know the probability any one of these occurred, we can sum them, to get (1+ 2 x 4 + 3 x 4)/81 = 21/81 = 7/27.
TMUA Paper 1 Practice Question 4
When is (sin2x)/(1 – cos2x)(3x -2) ≥ 0 in the range of 0 < x < π?
A) log32 ≤ x ≤ (π/2)
B) log32 < x < (π/2)
C) (π/2) < x ≤ log32
D) 0 < x < log32
E) (π/2) ≤ x ≤ log32
F) 0 < x ≤ log32
The correct answer is A.
Using trigonometric identities, cos2x = 1 – 2sin²x, sin2x = 2sinxcosx.
This means that sin2x/(1-cos2x) = cosx/sinx.
We then know the critical values of x are when cosx is equal to 0(x = nπ/2). The other part of the expression has only 1 critical value at x = log32. All that’s left to determine is whether they are positive or negative around these values.
(3x – 2) is increasing, so it must be below the x-axis before x == log32 and positive after. We only need to consider π/2 which is the only critical value in range for this problem, and both sinx and cosx are positive at x = 0, so the graph must be positive before x = π/2 and negative after. We are looking for where they have the same sign, and we know that log32 < 1(as log33 = 1) so it must be log32 ≤ x ≤ (π/2).
There’s a lot to revise for the TMUA, so why not get some help from TMUA.Ninja?
With our TMUA Preparation Platform, you can get access to guides and practice questions for all content of the TMUA. Click below to find out how you can optimise your TMUA revision.
3/3
TMUA PAPER 2
Paper 2 of the TMUA features questions that you may not be as used to. You’re going to need to implement skills in mathematical logic to get a good score here, so let’s see what you need to know!



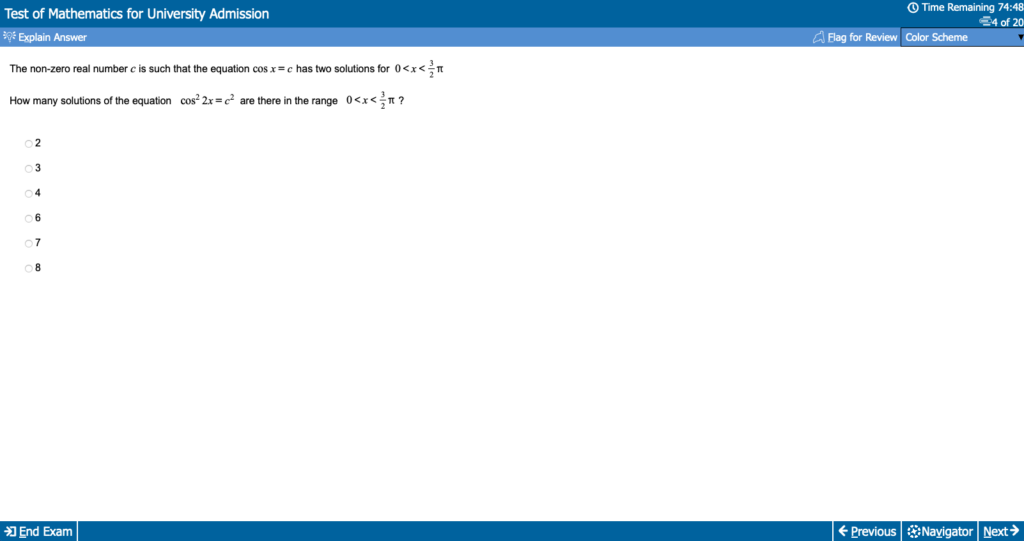
We’ve mention this a few times already, but it’s important to properly understand that Paper 2 of the TMUA does not feature the same style of mathematical questions as Paper 1. To properly understand why this is, let’s look at an example of a typical page in Paper 2:
TMUA Paper 2 Example Page
While the presentation is the exact same, the style of the question is different. Questions here are not about simply solving a problem, but using the solution to answer questions within the context of the question, or to evaluate a problem and/or solution and discuss it’s reasoning or its flaws.
This makes its sound like an entirely different subject than Paper 1, but the difference isn’t as extreme as you think. These are still undeniably maths questions, and as such you will be required to use maths to solve a problem. The key thing is that you will have extra steps and extra things to consider when doing so.
Even though the question may ask you to disprove a mathematical argument or explain a problem, you’re still going to be using the core principles of mathematics that you’ve been learning throughout the years.To understand this further, lets move on to the specification for Paper 2:
TMUA Paper 2 Specification
First things first: there is no new mathematical knowledge that will be required for this paper. Everything that will be included here is covered in Section 1 of the TMUA Specification. That will certainly make your revision a bit easier, as everything you need to know for both sections is covered there; at least in terms of pure maths.
As you could probably guess, the different style of questions for Paper 2 will require some different types of skills and techniques. These have all be outlined in the specification under Section 2, so let’s take a look at what you need to practice:
TMUA Specification: Section 2
The Logic of Argument
This is a concept that definitely isn’t unique to maths but will be required for a lot of the questions you’ll encounter during your revision and on testing day. Using this in mathematics may be slightly easier than a subject like politics however, as a Mathematica problem is always going to have an objectively correct solution.
Mathematical logic, as it’s called in the context of the TMUA, will be used for fairly simple scenarios here, so it’s not going to be too complex. Essentially, this will be your method of developing a correct statement to answer the question you’ve been asked. It will typically take a form like these:
If A then B
A if B
A only if B
A if and only if B
So for example, if x is odd, then x + 1 is even. Keep in mind that you will also need to understand the converse and contrapositive of your statement.
On the other side of this, you will need to be able to analyse statements included within questions that will ask you to prove or disprove them.
Some of the key terms of revise here include necessary, sufficient, for all, for some and there exists.
Mathematical Proof
All of these questions are multiple-choice, so you’re not going to need to be writing up full statements providing the proof of your findings. However, some questions will still relate to this in someway, whether it’s due to the question providing different forms of proof in its answers, or potentially asking you to disprove an argument due to missing or insubstantial proof.
There are different forms of proof that you’re going to need to consider include:
- Direct deductive proof
- Proof by cases
- Proof by contradiction
- Disproof by counter example
These are the key principles to mathematical proof highlighted by the specification:
- Deducing implications from given statements
- Rearranging statement sequences to give a correct order
- Using sophisticated chains of reasoning to solve
These will all be important techniques to practice when solving these questions.
Identifying Error in Proofs
This one is linked pretty closely to the last point, seeing as they both relate to mathematical proof. We touched on this briefly before, but some questions are going to require you to review a given sequence of statements or work in order to determine errors within them.
In the TMUA, this is referred to as identifying errors in purported proofs, as what you’re reviewing will be presented as the proof to a solution (basically the working out). Of course, there will be an error in there somewhere and your job could be one of various things.
You may be required to simply identify the mistake within the proof. However, the questions could potentially go further and ask you to determine how the error was caused in the first place, essentially finding the reasoning behind it. Of course, you may also be asked to correct the mistake and provide the actual solution to initial problem.
There are a few plenty of simple mathematical errors to keep an eye out for in purported proofs. A couple of examples given include the following statements:
If ab = ac, then b = c
If sina = sinb, then a = b
These are pretty simple mistakes, but they may be difficult to spot within the large sequences of statements that are typically featured in Paper 2 questions.
It’s pretty difficult to properly understand the use of all these techniques without seeing them in context, as these aren’t the kind of skills you can “revise” in a traditional sense. Our TMUA Paper 2 Guide goes into more detail about how you can tackle these questions effectively. However, practice is going to be the most important thing you can do to prepare.
Outside of the TMUA, this is a very uncommon style of question which means practicing it can be tricky. You’re unfortunately not going to be able to find many questions like this outside of TMUA practice materials and past papers, as neither the STEP or MAT exam have anything that compares to Paper 2. Therefore, you need to be careful not to use up all of your resources too early into your preparation timeline.
A practice test for the TMUA has been made available by UAT which uses the official testing programme. This is definitely worth trying out to get to grips with the programme, but be aware that the questions available in it are very limited.
It’s also good to take older past papers in proper exam conditions, but you won’t get as much out of this until you’ve effectively revised your knowledge and skills in a more casual setting. Of course, the best way to mitigate this problem is with TMUA.Ninja, which provides you with 100’s of additional practice questions and an easy-to-use exam simulator, including worked solutions for every question included.
TMUA Paper 2 Practice Questions
To get your practice started, let’s try out some practice questions and get a better idea of what to expect:
TMUA Paper 2 Practice Question 1
Consider the statement: “If n is an integer and n² is divisible by 4, then n is divisible by 4”.
How many counterexamples are there to this in the range 50 ≤ n ≤ 100.
A) 24
B) 25
C) 11
D) 12
E) 13
The correct answer is E.
Clearly we need to count the number of multiples of two, but not of four, in the range. So 50,54,58,…,98. There are 13.
TMUA Paper 2 Practice Question 2
A Pythagorean triple is where 3 positive integers, a, b and c fit the equation a² + b² = c².
The 2 smallest integers of a Pythagorean triple are 20 and 21. Find the third integer. Comparing this to the smallest Pythagorean triple, what is the highest common factor of the sum of the integers in both equations and the integer formed by the two largest numbers plus the 2 smallest numbers from both equations.
A) 1
B) 2
C) 3
D) 5
E) 7
F) 11
G) 13
H) 12
The correct answer is A.
20² + 21² = 29²
The smallest triple is 32 + 42 = 52. If this is not known, it can easily be worked out by writing down all the square numbers until you see 2 that will add to make another one.
Sum of the integers in both equations – 20 + 21 + 29 + 3 + 4 + 5 = 82.
Product of the two largest numbers minus the 2 smallest numbers from both equations = (29 +21) + (3+4) = 57.
HCF of 57 and 82:
82 factors: 1, 2, 41, 82
57 factors: 1, 3, 19, 57
HCF = 1
TMUA Paper 2 Practice Question 3
Consider the graphs of the two functions y = mx + 10 and y = log2x. Which of the following correctly identifies the sufficiency and necessity of:
- m < 0
- m > 10
in relation to the statement that there are intersection points of the two graphs?
A) Both necessary and sufficient.
B) Both necessary.
C) Both sufficient.
D) 1 is sufficient, the other is necessary.
E) Only 1 is necessary.
F) Only 1 is sufficient.
G) Neither is necessary or sufficient.
The correct answer is F.
We want the two graphs to intersect but equating the expressions won’t get us very far. Instead, a sketch of both graphs is more illuminating. The line intersects the y-axis at 10, which is much higher than the other line. The gradient of log2x is decreasing, and as the gradient of the straight line is constant, if it begins large enough, they will never meet. 10 is one such value and so anything larger will also never meet the curve. However, there are also slightly smaller values which would also work, so it is not necessary. For m negative, the line must proceed downwards from(0,10). One can see that, as eventually log2x = 10, even an almost flat decreasing straight line would intersect the curve. Thus, no matter the value of m, if it is negative, the lines must cross. So, 1 is sufficient, 2 is neither.
TMUA Paper 2 Practice Question 4
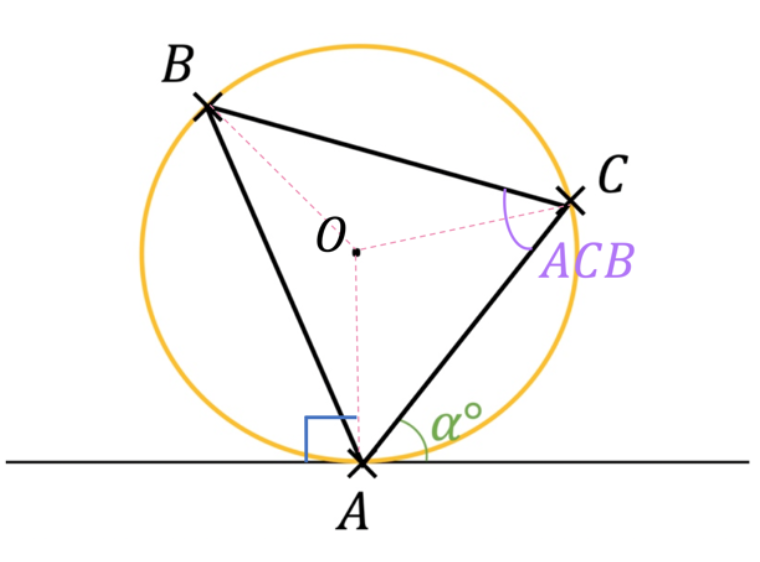
Consider the following proof of the alternate segment theorem:
- Let a tangent touch a circle at A and let B, C be two points on the circumference of the circle. Let the angle between the line CA and the tangent b α°.
- By drawing radii from C & A to the centre of the circle, which we will call O, we know that the angle between OA and the tangent is 90°.
- This means the angle BAO is (90 – α)°.
- Since the triangle OBA is isosceles, the angle OBA is also (90 – α)°.
- Then the angle AOB is 180° – (180 – 2α)° = 2α°
- This means the angle ACB is (2α/2)° = α°.
Where is the first error?
A) The proof is correct
B) Line 1
C) Line 2
D) Line 3
E) Line 4
F) Line 5
The correct answer is C.
By drawing the circle and tangent, the error becomes relatively clear. The angle that would be equal to α using the alternate segment theorem would be ABC, not ACB as is calculated in the question, so the result is clearly false. To find the error, notice that angle BAO has nothing to do with α, and it is in fact angle CAO that is(90 – α)º. So, the error is on line III.
These practice questions should highlight how different these questions can be to what you’re used to, but should also show you the similarities and ease your concerns about them. Remember; it’s still maths, it’s just presented a bit differently and requires a slightly different viewpoint. As long as your maths knowledge is on point, you shouldn’t face any major problems (you still need to practice, of course!)
TMUA Final Tips
Here are a few final tips to help you with your preparation and exam techniques:
- Plan your revision ahead of time, the benefits will become obvious as soon as you start!
- Gather as many resources as possible. TMUA resources currently aren’t the easiest to find so don’t leave this to the last minute (TMUA.Ninja is most likely the best option!).
- Learn your equations off by heart, these will be essential for many of the questions included.
- As you get closer to the exam, you definitely need to take regular mock exams with past papers or practice questions. They will help you get used to the time limits of the exam.
- In the exam, don’t be afraid to leave particularly difficult questions for the end. With only 20 questions to do in 75 minutes, you’re more than likely going to have enough time come back to them.
- Be sure to leave an answer for every question in the test, even if it’s just a guess. There’s no negative marking so you need to give yourself the chance to get the mark.
- You can flag questions at any time if you want to come back to them before the end of the paper. This is a very helpful tool if you aren't sure of an answer and want more time to solve it at the end, but be sure to select and answer before you move on, even if it's a guess.
So, that completes the first step of your TMUA preparation. You now have a good understanding of what the TMUA actually is and what it’s going to test you on, so the next step is to begin your revision. We would recommend checking out more of our TMUA guides or trying out our free TMUA.Ninja demo, which will let you trial our extensive suite of tutorials, practice questions and past papers! Whatever you decide to do, be sure to revise consistently up until testing day to give yourself the best chance of success!
Combine all your TMUA preparation in one comprehensive package instantly with Exams.Ninja.
Exams.Ninja’s TMUA Preparation Platform allows you to optimise all areas of your revision in one easy to use platform. With the Preparation Platform, you’ll get access to:
Training Temple – over 100 expert tutorials about the TMUA, including content knowledge guides, tips and much more to guide you every step of the way.
Practice Dojo – over 500 practice questions, each one matching the difficulty of real TMUA questions with fully worked solutions to help you understand everything you need to know.
Exam Arena – Attempt 5 full TMUA past papers in a real exam scenario. See where you’re at and how you will do on the real thing.
Sign up today for free to maximise your chances of success!