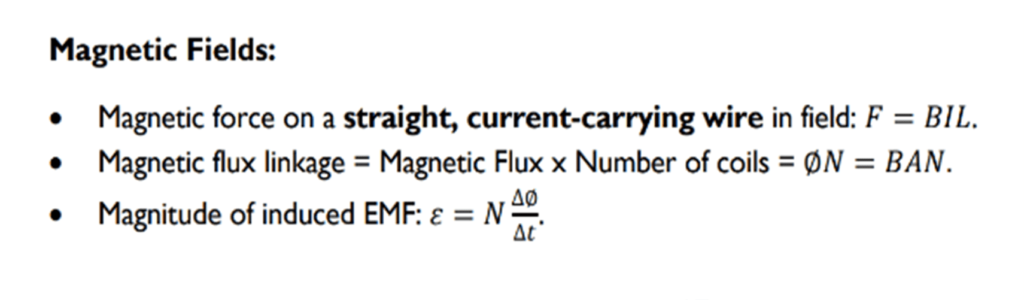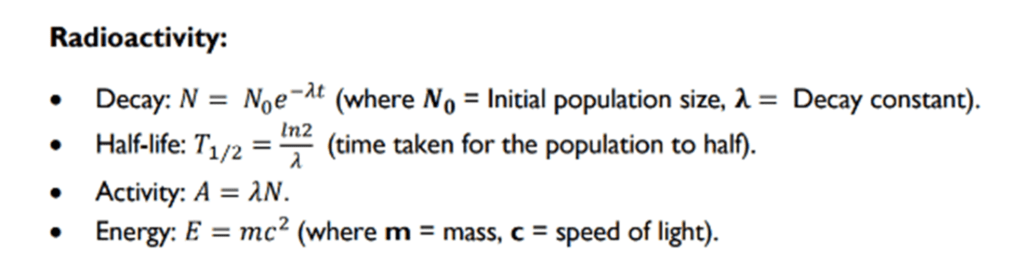ENGAA GUIDE
The Definitive Guide To The ENGAA Section 1A: Mathematics and Physics
Written by: Matt Amalfitano-Stroud
Please be aware that, as of 2024, the Engineering Admissions Assessment (ENGAA) is no longer being used by the University of Cambridge. Cambridge applicants for Natural Sciences, Engineering, Veterinary Medicine and Chemical Engineering & Biotechnology will be required to sit the Engineering and Science Admissions Test (ESAT).
So, you’re about to dive deep into the Engineering Admissions Assessment (ENGAA). Your first challenge is the Maths and Physics Section, a 20 multiple choice question threat that doesn’t allow a calculator to defeat! Don’t fret, Exams. Ninja is here to give you vital tips, tricks, practice questions and more so you can tackle Section 1A effectively.
1/5
BASICS OF THE ENGAA
Before we dive into Section 1A, let’s recap what we need to know about the ENGAA as a whole.


What is the ENGAA?
If you’ve not come across the ENGAA structure before, here’s a quick recap:
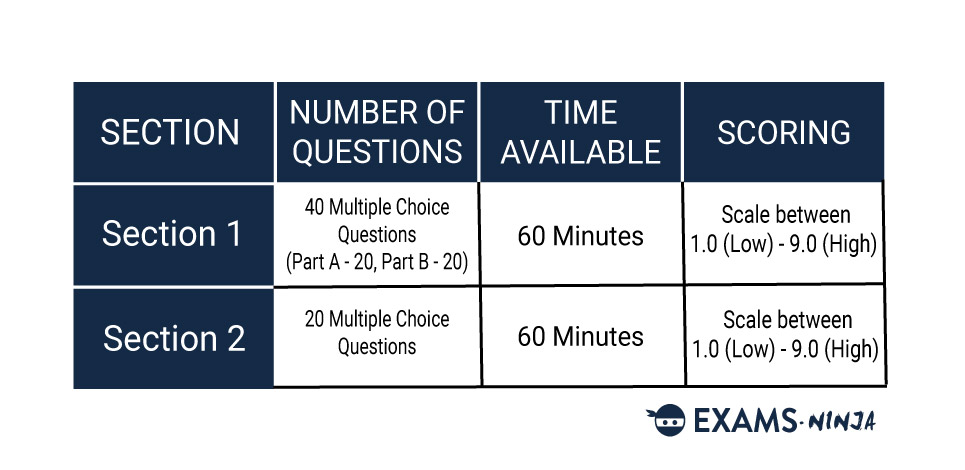
ENGAA Test Format
The ENGAA is sat by applicants of Engineering at the University of Cambridge on October 18th 2023, which is around two weeks earlier than in previous years.
The ENGAA consists of two papers sat back-to-back, Section 1 and 2. Each paper is made up of multiple-choice questions that cover topics from mathematics and physics at both a basic and advanced level.
Section 1 is split into two parts that cover both basic and advances maths and physics, with 20 questions to answer for each.
Section 2 consist of just one part, with just 20 questions on the paper. All of these questions will revolve around Advanced Physics. It’s not just a simple repeat of Section 1B however, so we’d recommend you check out our ENGAA Section 2 Guide to find out more about what you’ll be doing in the second half of the exam.
You’ll have one hour to complete each section, making the exam last two hours in total. Remember, you won’t be allowed a calculator or any other form of supporting material for any of the sections of the exam.
How is the ENGAA Scored?
The ENGAA is scored based on the amount of correct answers you get, there is no penalty for incorrect answers. Each Section will be scored separately on a scale of 1.0 – 9.0, with Section 1 receiving one score for each of the two parts you complete.
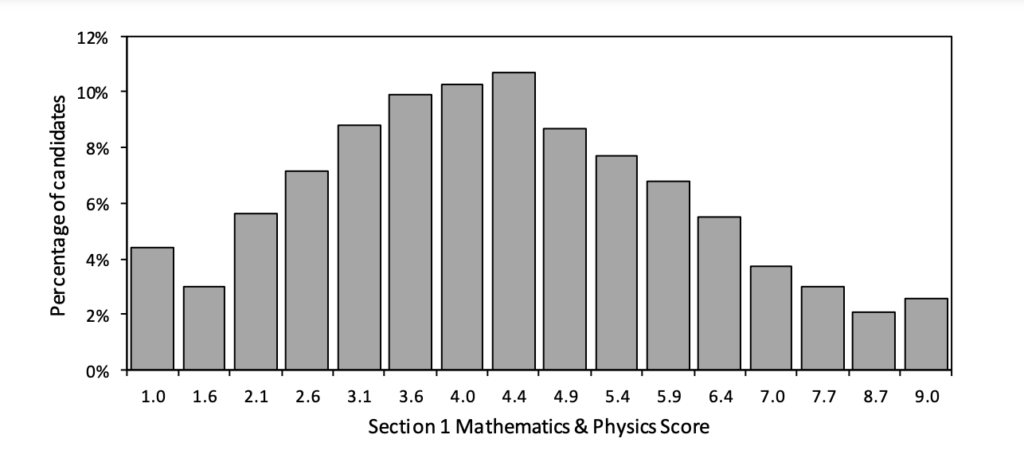
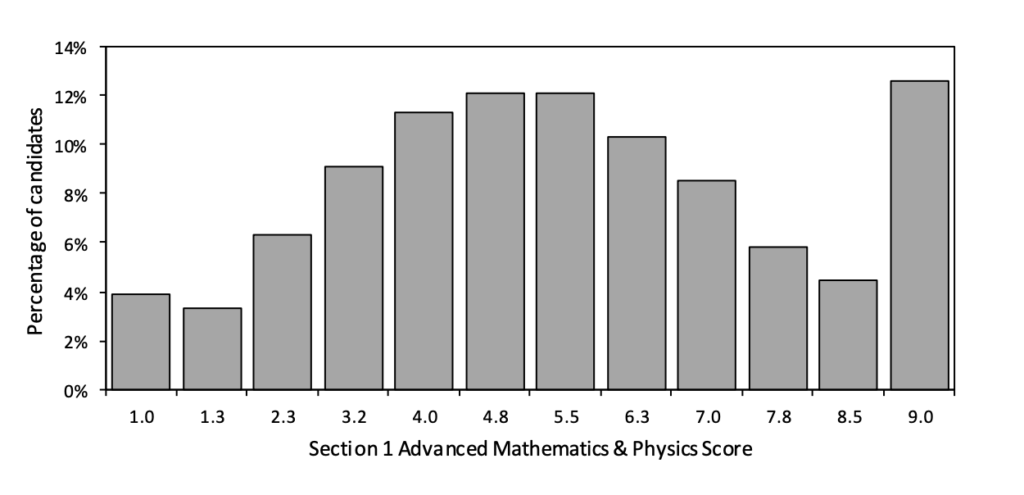
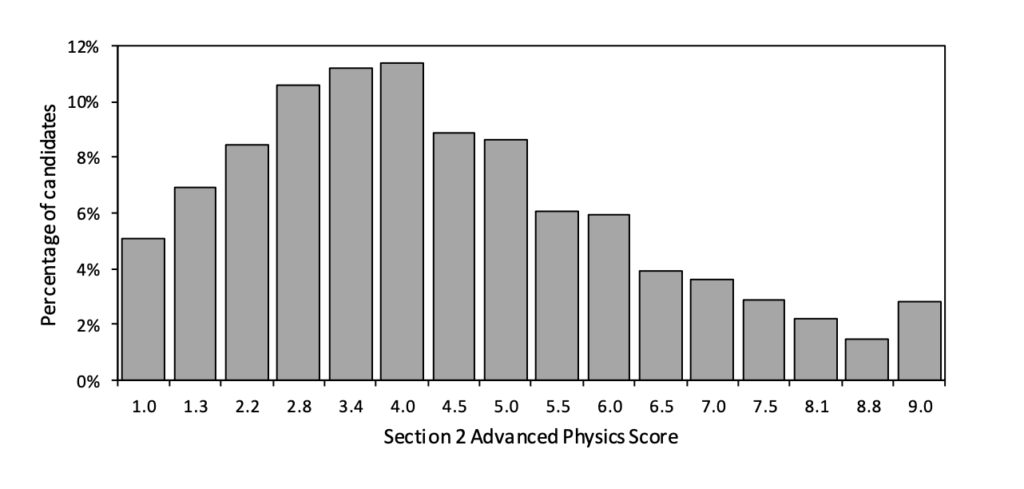
Below you can see the Distribution of Scores for applicants in the 2021 exam cycle.
ENGAA Section 1A Score Distribution 2021
ENGAA Section 1B Score Distribution 2021
ENGAA Section 2 Score Distribution 2021
You can see there’s a clear trend in each Section as to what the most common score is, which can be used to assess the difficulty of each part of the exam. For example, it’s clear that Section 2 is the more difficult of the two papers, with applicants generally scoring less compared to both parts of Section 1.
You can find more information about the full ENGAA in our Definitive Guide.
There’s no better time to start your ENGAA preparation than now!
Utilise over 900 exam quality questions, each with comprehensive solutions to help you always learn the correct answer. We make sure that the difficulty of the questions matches that of the real exam. Always practice for the real thing. So, why not start for free?
2/5
WHAT TO EXPECT FROM THE ENGAA SECTION 1A
Now let’s have a look at Section 1 is laid out, and what we need to know for Section 1A specifically.
The ENGAA is designed for students who are currently in the process of completing their Maths and Physics A-Levels.
What does this mean?
It means that you are expected to have an excellent knowledge of GCSE Maths and Physics and a good standard of knowledge in A-levels Maths and Physics too.
Section 1A is made up of 20 multiple choice maths and physics questions. 1B follows up with Advanced Maths and Physics questions. You have 60 minutes for Section 1 and since Section 1 is split between 1A and 1B, you have approx. 30 minutes per part and 90 seconds per question.
Here’s a standard example of what a page from the Section 1 paper will look like:
ENGAA Section 1A Example Page
Each page of the question book will contain one or two questions depending on their size. Pages should provide you with enough empty space to write down your working out, which you will need to do as no extra paper is provided for rough work, nor is rough work allowed on your answer sheet.
We have a complete guide on the ENGAA which covers literally everything if you are looking to learn about the other sections too!
What Does Section 1A Require?
As mentioned above, applicants should have expert knowledge in GCSE Maths and Physics and a good grasp of A-Level Maths and Physics. Overall, the ENGAA is a tough exam. You may do well if you are amazing in Maths and Physics but the time constraints make the exam even more difficult.
In order to explain what is required, here is the syllabus for both Maths and Physics outlined below:
Complete ENGAA Maths Syllabus
| M1.1 | Use standard units of mass, length, time, money and other measures. Use compound units such as speed, rates of pay, unit pricing, density and pressure, including using decimal quantities where appropriate. |
|---|---|
| M1.2 | Change freely between related standard units (e.g. time, length, area, volume/capacity, mass) and compound units (e.g. speed, rates of pay, prices, density, pressure) in numerical and algebraic contexts. |
| M2.1 | Order positive and negative integers, decimals and fractions. Understand and use the symbols: = , ≠ , < , > , ≤ , ≥ . |
|---|---|
| M2.2 | Apply the four operations (addition, subtraction, multiplication and division) to integers, decimals, simple fractions (proper and improper) and mixed numbers – any of which could be positive and negative. Understand and use place value. |
| M2.3 | Use the concepts and vocabulary of prime numbers, factors (divisors), multiples, common factors, common multiples, highest common factor, lowest common multiple, and prime factorisation (including use of product notation and the unique factorisation theorem). |
| M2.4 | Recognise and use relationships between operations, including inverse operations. Use cancellation to simplify calculations and expressions. Understand and use the convention for priority of operations, including brackets, powers, roots and reciprocals. |
| M2.5 | Apply systematic listing strategies. (For instance, if there are m ways of doing one task and for each of these tasks there are n ways of doing another task, then the total number of ways the two tasks can be done in order is m× n ways.) |
| M2.6 | Use and understand the terms: square, positive and negative square root, cube and cube root. |
| M2.7 | Use index laws to simplify numerical expressions, and for multiplication and division of integer, fractional and negative powers. |
| M2.8 | Interpret, order and calculate with numbers written in standard index form (standard form); numbers are written in standard form as a × 10n, where 1 ≤ a < 10 and n is an integer. |
| M2.9 | Convert between terminating decimals, percentages and fractions. Convert between recurring decimals and their corresponding fractions |
| M2.10 | Use fractions, decimals and percentages interchangeably in calculations. Understand equivalent fractions. |
| M2.11 | Calculate exactly with fractions, surds and multiples of π. Simplify surd expressions involving squares, e.g. √12 = √4 x 3 = √4√3 = 2√3, and rationalise denominators; for example, candidates could be asked to rationalise expressions such as: 3 / √7, 5 / 3 + 2√5, 7 / 2 – √3, 3 / √5 – √2. |
| M2.12 | Calculate with upper and lower bounds, and use in contextual problems. |
| M2.13 | Round numbers and measures to an appropriate degree of accuracy, e.g. to a specified number of decimal places or significant figures. Use inequality notation to specify simple error intervals due to truncation or rounding. |
| M2.14 | Use approximation to produce estimates of calculations, including expressions involving π or surds. |
| M3.1 | Understand and use scale factors, scale diagrams and maps. |
|---|---|
| M3.2 | Express a quantity as a fraction of another, where the fraction is less than 1 or greater than 1. |
| M3.3 | Understand and use ratio notation. |
| M3.4 | Divide a given quantity into two (or more) parts in a given part:part ratio. Express the division of a quantity into two parts as a ratio. |
| M3.5 | Apply ratio to real contexts and problems, such as those involving conversion, comparison, scaling, mixing and concentrations. Express a multiplicative relationship between two quantities as a ratio or a fraction. |
| M3.6 | Understand and use proportion. Relate ratios to fractions and to linear functions. |
| M3.7 | Identify and work with fractions in ratio problems. |
| M3.8 | Define percentage as ‘number of parts per hundred’. Interpret percentages and percentage changes as a fraction or a decimal, and interpret these multiplicatively. Express one quantity as a percentage of another. Compare two quantities using percentages. Work with percentages greater than 100%. Solve problems involving percentage change, including percentage increase/decrease, original value problems and simple interest calculations. |
| M3.9 | Understand and use direct and inverse proportion, including algebraic representations. Recognise and interpret graphs that illustrate direct and inverse proportion. Set up, use and interpret equations to solve problems involving direct and inverse proportion (including questions involving integer and fractional powers). Understand that x is inversely proportional to y is equivalent to x is proportional to 1 / y. |
| M3.10 | Compare lengths, areas and volumes using ratio notation. Understand and make links to similarity (including trigonometric ratios) and scale factors |
| M3.11 | Set up, solve and interpret the answers in growth and decay problems, including compound interest, and work with general iterative processes. |
| M4.1 | Understand, use and interpret algebraic notation; for instance: ab in place of a×b ; 3y in place of y+y+y and 3 × y ; a2 in place of a×a ; a3 in place of a×a×a ; a2b in place of a×a×b ; a / b in place of a ÷ b |
|---|---|
| M4.2 | Use index laws in algebra for multiplication and division of integer, fractional, and negative powers. |
| M4.3 | Substitute numerical values into formulae and expressions, including scientific formulae. Understand and use the concepts and vocabulary: expressions, equations, formulae, identities, inequalities, terms and factors. |
| M4.4 | Collect like terms, multiply a single term over a bracket, take out common factors, and expand products of two or more binomials. |
| M4.5 | Factorise quadratic expressions of the form x2 + bx +c, including the difference of two squares. Factorise quadratic expressions of the form ax2 + bx +c, including the difference of two squares. |
| M4.6 | Simplify expressions involving sums, products and powers, including the laws of indices. Simplify rational expressions by cancelling, or factorising and cancelling. Use the four rules on algebraic rational expressions. |
| M4.7 | Rearrange formulae to change the subject. |
| M4.8 | Understand the difference between an equation and an identity. Argue mathematically to show that algebraic expressions are equivalent |
| M4.9 | Work with coordinates in all four quadrants. |
| M4.10 | Identify and interpret gradients and intercepts of linear functions ( y = mx + c ) graphically and algebraically. Identify pairs of parallel lines and identify pairs of perpendicular lines, including the relationships between gradients. Find the equation of the line through two given points, or through one point with a given gradient. |
| M4.11 | Identify and interpret roots, intercepts and turning points of quadratic functions graphically. Deduce roots algebraically, and turning points by completing the square. |
| M4.12 | Recognise, sketch and interpret graphs of: a. linear functions b. quadratic functions c. simple cubic functions d. the reciprocal function: y = x / 1 with x≠0 e. the exponential function: y = kx for positive values of k f. trigonometric functions (with arguments in degrees): y = sin x, y = cos x, y = tan x for angles of any size |
| M4.13 | Interpret graphs (including reciprocal graphs and exponential graphs) and graphs of non-standard functions in real contexts to find approximate solutions to problems, such as simple kinematic problems involving distance, speed and acceleration. |
| M4.14 | Calculate or estimate gradients of graphs and areas under graphs (including quadratic and other non-linear graphs), and interpret results in cases such as distance–time graphs, speed–time graphs and graphs in financial contexts. |
| M4.15 | Set up and solve, both algebraically and graphically, simple equations including simultaneous equations involving two unknowns; this may include one linear and one quadratic equation. Solve two simultaneous equations in two variables (linear/linear or linear/quadratic) algebraically. Find approximate solutions using a graph. Translate simple situations or procedures into algebraic expressions or formulae; for example, derive an equation (or two simultaneous equations), solve the equation(s) and interpret the solution. |
| M4.16 | Solve quadratic equations (including those that require rearrangement) algebraically by factorising, by completing the square, and by using the quadratic formula. Know the quadratic formula: x = – b ± √b2 – 4ac / 2a Find approximate solutions of quadratic equations using a graph. |
| M4.17 | Solve linear inequalities in one or two variables. Represent the solution set on a number line, or on a graph, or in words. |
| M4.18 | Generate terms of a sequence using term-to-term or position-to-term rules. |
| M4.19 | Deduce expressions to calculate the nth term of linear or quadratic sequences. |
| M5.1 | Use conventional terms and notation: points, lines, line segments, vertices, edges, planes, parallel lines, perpendicular lines, right angles, subtended angles, polygons, regular polygons and polygons with reflection and/or rotational symmetries. |
|---|---|
| M5.2 | Recall and use the properties of angles at a point, angles on a straight line, perpendicular lines and opposite angles at a vertex. Understand and use the angle properties of parallel lines, intersecting lines, triangles and quadrilaterals. Calculate and use the sum of the interior angles, and the sum of the exterior angles, of polygons. |
| M5.3 | Derive and apply the properties and definitions of special types of quadrilaterals, including square, rectangle, parallelogram, trapezium, kite and rhombus. Derive and apply the properties and definitions of various types of triangle and other plane figures using appropriate language. |
| M5.4 | Understand and use the basic congruence criteria for triangles (SSS, SAS, ASA, RHS). |
| M5.5 | Apply angle facts, triangle congruence, similarity, and properties of quadrilaterals to results about angles and sides. |
| M5.6 | Identify, describe and construct congruent and similar shapes, including on coordinate axes, by considering rotation, reflection, translation and enlargement (including fractional and negative scale factors). Describe the changes and invariance achieved by combinations of rotations, reflections and translations. Describe translations as 2-dimensional vectors. |
| M5.7 | Know and use the formula for Pythagoras’ theorem: a2 + b2 = c2 Use Pythagoras’ theorem in both 2 and 3 dimensions. |
| M5.8 | Identify and use conventional circle terms: centre, radius, chord, diameter, circumference, tangent, arc, sector and segment (including the use of the terms minor and major for arcs, sectors and segments). |
| M5.9 | Apply the standard circle theorems concerning angles, radii, tangents and chords, and use them to prove related results: a. angle subtended at the centre is twice the angle subtended at the circumference b. angle in a semicircle is 90° c. angles in the same segment are equal d. angle between a tangent and a chord (alternate segment theorem) e. angle between a radius and a tangent is 90° f. properties of cyclic quadrilaterals |
| M5.10 | Solve geometrical problems on 2-dimensional coordinate axes. |
| M5.11 | Know the terminology faces, surfaces, edges and vertices when applied to cubes, cuboids, prisms, cylinders, pyramids, cones, spheres and hemispheres. |
| M5.12 | Interpret plans and elevations of 3-dimensional shapes. |
| M5.13 | Use and interpret maps and scale drawings. Understand and use three-figure bearings. |
| M5.14 | Know and apply formulae to calculate: a. the area of triangles, parallelograms, trapezia b. the volume of cuboids and other right prisms. |
| M5.15 | Know the formulae: a. circumference of a circle = 2πr = πd b. area of a circle = πr2 c. volume of a right circular cylinder = πr2h Formulae relating to spheres, pyramids and cones will be given if needed. Use formulae to calculate: a. perimeters of 2-dimensional shapes, including circles b. areas of circles and composite shapes c. surface area and volume of spheres, pyramids, cones and composite solids |
| M5.16 | Calculate arc lengths, angles and areas of sectors of circles. |
| M5.17 | Apply the concepts of congruence and similarity in simple figures, including the relationships between lengths, areas and volumes. |
| M5.18 | Know and use the trigonometric ratios: sinθ = opposite / hypotenuse cosθ = adjacent / hypotenuse tanθ = opposite / adjacent Apply these to find angles and lengths in right-angled triangles and, where possible, general triangles in 2- and 3-dimensional figures. Know the exact values of sinθ and cosθ for θ = 0°, 30°, 45°, 60°, 90°. Know the exact values of tanθ for θ = 0°, 30°, 45°, 60°. Candidates are not expected to recall or use the sine or cosine rules. |
| M5.19 | Apply addition and subtraction of vectors, multiplication of vectors by a scalar, and diagrammatic and column representations of vectors. Use vectors to construct geometric arguments and proofs. |
| M6.1 | Interpret and construct tables, charts and diagrams, including: a. two-way tables, frequency tables, bar charts, pie charts and pictograms for categorical data b. vertical line charts for ungrouped discrete numerical data c. tables and line graphs for time series data Know the appropriate use of each of these representations. |
|---|---|
| M6.2 | Interpret and construct diagrams for grouped discrete data and continuous data: a. histograms with equal and unequal class intervals b. cumulative frequency graphs Know the appropriate use of each of these diagrams. Understand and use the term frequency density. |
| M6.3 | Calculate the mean, mode, median and range for ungrouped data. Find the modal class; calculate estimates of the range, mean and median for grouped data, and understand why these are estimates. Describe a population using statistics. Make simple comparisons. Compare data sets using like-for-like summary values. Understand the advantages and disadvantages of summary values. Calculate estimates of mean, median, mode, range, quartiles and interquartile range from graphical representation of grouped data. Use the median and interquartile range to compare distributions. |
| M6.4 | Use and interpret scatter graphs of bivariate data. Recognise correlation, and know that it does not indicate causation. Draw estimated lines of best fit. Interpolate and extrapolate apparent trends whilst knowing the dangers of so doing. |
| M6.1 | Analyse the frequency of outcomes of probability experiments using tables and frequency trees. |
|---|---|
| M6.2 | Apply ideas of randomness, fairness and equally likely events to calculate expected outcomes of multiple future experiments. Understand that if an experiment is repeated, the outcome may be different. |
| M6.3 | Relate relative expected frequencies to theoretical probability, using appropriate language and the ‘0 to 1’ probability scale. |
| M6.4 | Apply the property that the probabilities of an exhaustive set of outcomes sum to one. Apply the property that the probabilities of an exhaustive set of mutually exclusive events sum to one. |
| M6.5 | Enumerate sets and combinations of sets systematically, using tables, grids, Venn diagrams and tree diagrams. Candidates are not expected to know formal set theory notation. |
| M6.6 | Construct theoretical possibility spaces for single and combined experiments with equally likely outcomes, and use these to calculate theoretical probabilities. |
| M6.7 | Know when to add or multiply two probabilities, and understand conditional probability. Calculate and interpret conditional probabilities through representation using expected frequencies with two-way tables, tree diagrams and Venn diagrams. Understand the use of tree diagrams to represent outcomes of combined events: a. when the probabilities are independent of the previous outcome b. when the probabilities are dependent on the previous outcome. |
Complete ENGAA Physics Syllabus
| P1.1 | Electrostatics: a. Know and understand that insulators can be charged by friction b. Know and understand that charging is caused by gain or loss of electrons c. Know and understand that like charges repel and unlike charges attract d. Understand applications and hazards associated with electrostatics, including the role of earthing |
|---|---|
| P1.2 | Electric circuits: a. Know and recognise the basic circuit symbols and diagrams, including: cell, battery, light source, resistor, variable resistor, ammeter, voltmeter, switch, diode b. Understand the difference between alternating current (ac) and direct current (dc) c. Understand the difference between conductors and insulators, and recall examples of each type d. Know and be able to apply: current = charge/time, I = V / I e. Know and understand the use of voltmeters and ammeters f. Know and be able to apply: resistance = voltage/current, R = V / I g. Recall and interpret V–I graphs for a fixed resistor and a filament lamp h. Know the properties of NTC (negative temperature coefficient) thermistors, LDRs (light-dependent resistors) and ideal diodes i. Know and understand the current and voltage rules for series and parallel circuits j. Calculate the total resistance for resistor combinations in series k. Understand that the total resistance of a parallel combination is less than that of any individual resistor l. Know and be able to apply: voltage = energy/charge, V = E / Q m. Know and be able to apply: power = current × voltage, P = IV = I2 R n. Know and be able to apply: energy transfer = power × time, E =VIt |
| P2.1 | Properties of magnets: a. Know and be able to use the terms north pole, south pole, attraction and repulsion b. Know the magnetic field pattern around a bar magnet (including direction) c. Understand the difference between soft and hard magnetic materials (e.g. iron and steel) d. Qualitatively understand induced magnetism |
|---|---|
| P2.2 | Magnetic field due to an electric current: a. Know and understand the magnetic effect of a current b. Know the magnetic field patterns around current-carrying wires (including direction) for straight wires and coils/solenoids c. Know and understand the factors affecting magnetic field strength around a wire d. Understand the difference between permanent magnets and electromagnets |
| P2.3 | The motor effect: a. Know that a wire carrying a current in a magnetic field can experience a force b. Know the factors affecting the direction of a force on a wire in a magnetic field (including the left-hand rule) c. Know the factors affecting the magnitude of the force on a wire in a magnetic field d. Know and be able to apply F=BIL for a straight wire at right angles to a uniform magnetic field e. Know and understand the construction and operation of a dc motor, including factors affecting the magnitude of the force produced f. Understand applications of electromagnets |
| P2.4 | Electromagnetic induction: a. Know and understand that a voltage is induced when a wire cuts magnetic field lines, or when a magnetic field changes b. Know the factors affecting the magnitude of an induced voltage c. Know the factors affecting the direction of an induced voltage d. Understand the operation of an ac generator, including factors affecting the output voltage e. Interpret the graphical representation of the output voltage of a simple ac generator f. Understand applications of electromagnetic induction |
| P2.5 | Transformers: a. Know and understand the terms step-up transformer and step-down transformer b. Know and use the relationship between the number of turns on the primary and secondary coils, and the voltage ratio: Vp / Vs = np / ns c. Know that a consequence of 100% efficiency is total transfer of electrical power, and that this gives rise to the following relationship: VpIp = VsIs. Know and use this relationship to solve problems d. Understand power transmission, including calculating losses during transmission and the need for high voltage |
| P3.1 | Kinematics: a. Know and understand the difference between scalar and vector quantities b. Know and understand the difference between distance and displacement and between speed and velocity c. Know and be able to apply: speed = distance / time , velocity = change in displacement / time d. Know and be able to apply: acceleration = change in velocity / time e. Interpret distance–time, displacement–time, speed–time and velocity–time graphs f. Perform calculations using gradients and areas under graphs g. Know and be able to apply: average speed = total distance / time h. Know and be able to apply the equation of motion: v2 – u2 = 2as |
|---|---|
| P3.2 | Forces: a. Understand that there are different types of force, including weight, normal contact, drag (including air resistance), friction, magnetic, electrostatic, thrust, upthrust, lift and tension b. Know and understand the factors that can affect the magnitude and direction of the forces in 3.2a c. Draw and interpret force diagrams d. Qualitatively understand resultant force, with calculations in one dimension |
| P3.3 | Force and extension: a. Interpret force–extension graphs b. Understand elastic and inelastic extension, and elastic limits c. Know and be able to apply Hooke’s law (F = kx), and understand the meaning of the limit of proportionality d. Understand energy stored in a stretched spring as: E = 1/2 Fx = 1/2 kx2 |
| P3.4 | Newton’s laws: a. Know and understand Newton’s first law as: ‘a body will remain at rest or in a state of uniform motion in a straight line unless acted on by a resultant external force’ b. Understand mass as a property that resists change in motion (inertia) c. Know and understand Newton’s second law as: force = mass × acceleration d. Know and understand Newton’s third law as: ‘if body A exerts a force on body B then body B exerts an equal and opposite force of the same type on body A’ |
| P3.5 | Mass and weight: a. Know and understand the difference between mass and weight b. Know and be able to apply gravitational field strength, g, approximated as 10 Nkg–1 on Earth c. Know and be able to apply the relationship between mass and weight: w = mg d. Understand free-fall acceleration e. Know the factors affecting air resistance f. Understand terminal velocity and the forces involved |
| P3.6 | Momentum: a. Know and be able to apply: momentum = mass × velocity, p = mv b. Know and be able to use the law of conservation of momentum in calculations in one dimension c. Know and be able to apply: force = rate of change of momentum |
| P3.7 | Energy: a. Know and be able to apply: work = force × distance moved (in direction of force) b. Understand work done as a transfer of energy c. Know and be able to apply: gravitational potential energy = mgh, where h is the difference in height of the object d. Know and be able to apply: kinetic energy = 1/2mv2 e. Know and be able to apply: power = energy transfer / time f. Know and be able to use in calculations the law of conservation of energy g. Understand the concepts of useful energy and wasted energy h. Know and be able to apply: percentage efficiency = useful output / total output x 100 |
| P4.1 | Conduction: a. Know and understand thermal conductors and insulators, with examples b. Know and be able to apply factors affecting rate of conduction |
|---|---|
| P4.2 | Convection: a. Understand and be able to apply the effect of temperature on density of fluid b. Understand and be able to apply fluid flow caused by differences in density |
| P4.3 | Thermal radiation: a. Understand thermal radiation as electromagnetic waves in the infrared region b. Know and be able to apply absorption and emission of radiation c. Know and be able to apply factors affecting rate of absorption and emission of thermal radiation |
| P4.4 | Heat capacity: a. Understand the effect of energy transferred to or from an object on its temperature b. Know and be able to apply: specific heat capacity = thermal energy / mass x temprature change where temperature is measured in °C and specific heat capacity, c, is measured in J kg–1 °C–1 |
| P5.1 | States of matter: a. Know the characteristic properties of solids, liquids and gases b. Know and be able to apply particle models of solids, liquids and gases c. Know and be able to explain properties of solids, liquids and gases in terms of particle motion and the forces and distances between the particles |
|---|---|
| P5.2 | Ideal gases: a. Be able to explain pressure and temperature in terms of the behaviour of particles b. Understand and be able to apply the effect of pressure (P) on gas volume (V) constant temperature, i.e. PV = constant |
| P5.3 | State changes: a. Understand the terms melting point and boiling point b. Know and understand the terms latent heat of fusion and latent heat of vaporisation c. Know and be able to apply specific latent heat calculations. |
| P5.4 | Density: a. Know and be able to apply: density = mass / volume , p = m / v b. Understand the experimental determination of densities c. Be able to compare the densities of solids, liquids and gases |
| P5.5 | Pressure: a. Know and be able to apply: pressure = force / area b. Know and be able to apply: hydrostatic pressure = hρg, where h is the height, or depth, of the liquid |
| P6.1 | Wave properties: a. Understand the transfer of energy without net movement of matter b. Know and understand transverse and longitudinal waves c. Know and understand the terms: peak, trough, compression and rarefaction. d. Recall examples of waves, including electromagnetic waves and sound e. Know and be able to use the terms: amplitude, wavelength, frequency and f. period g. Know and be able to apply: frequency = 1 / period , f = 1 / T h. Know and be able to apply: wave speed = frequency × wavelength, v = fλ |
|---|---|
| P6.2 | Wave behaviour: a. Know and understand reflection at a surface b. Know and understand refraction at a boundary c. Know and understand the effect of reflection and refraction on the speed, frequency, wavelength and direction of waves d. Know and understand the analogy of reflection and refraction of light with that of water waves e. Know and understand the Doppler effect |
| P6.3 | Optics: a. Draw and interpret ray diagrams to describe reflection in plane mirrors b. Know and be able to apply: angle of incidence = angle of reflection c. Draw and interpret ray diagrams for refraction at a planar boundary d. Know and be able to interpret angle of incidence and angle of refraction e. Know and understand the effect of refraction on wave direction (away from or towards the normal) and speed (increasing or decreasing) |
| P6.4 | Sound waves: a. Understand the production of sound waves by a vibrating source b. Understand the need for a medium c. Understand qualitatively the relation of loudness to amplitude and pitch to frequency d. Know and understand longitudinal waves. e. Understand that reflection causes echoes e. Recall that the range of human hearing is 20Hz to 20 kHz f. Know and understand ultrasound and its uses (sonar and medical scanning) |
| P6.5 | Electromagnetic spectrum: a. Know and understand the nature and properties of electromagnetic waves (they are transverse waves and travel at the speed of light in a vacuum) b. Recall the component parts of the spectrum (radio waves, microwaves, IR, visible light, UV, X-rays, gamma) c. Understand the distinction of the component parts by different wavelengths and/or frequencies d. Recall the order of the component parts by wavelength and/or frequency e. Understand applications and hazards of the component parts of the electromagnetic spectrum |
| P7.1 | Atomic structure: a. Understand the atom in terms of protons, neutrons and electrons b. Know and be able to apply the nuclear model of atomic structure c. Know the relative charges and masses of protons, neutrons and electrons d. Understand and be able to use the terms atomic number and mass number e. Know and understand the term isotope f. Know and understand the term nuclide, and use nuclide notation g. Understand that ionisation is caused by the gain/loss of electrons |
|---|---|
| P7.2 | Radioactive decay: a. Know and understand that emissions arise from an unstable nucleus b. Know and understand the random nature of emissions c. Know and understand the differences between alpha, beta and gamma emission d. Know and understand the nature of alpha and beta particles, and gamma radiation e. Be able to use and interpret nuclear equations f. Know the effect of decay on atomic number and mass number |
| P7.3 | Ionising radiation: a. Know the relative penetrating abilities of alpha, beta and gamma radiation b. Know the relative ionising abilities of alpha, beta and gamma radiation c. Understand qualitatively the deflection of alpha, beta and gamma radiation in electric or magnetic fields d. Know and appreciate the existence of background radiation e. Understand the applications and hazards of ionising radiation |
| P7.4 | Half-life: a. Be able to interpret graphical representations of radioactive decay (including consideration of decay products) b. Understand the meaning of the term half-life c. Understand and be able to apply half-life calculations |
3/5
HOW TO GET A GOOD SCORE IN SECTION 1A OF THE ENGAA
What can you do to improve your preparations for the ENGAA and increase your chances of getting that dream offer? Let’s find out!
In order to score highly in Section 1A, here are some points to consider.
Firstly, and most importantly, past papers are crucial. Completing these in exam conditions is the best practice. This will also give you a realistic idea of what the exam will be like. You can learn more about how to create a preparation plan, including past papers, with our ENGAA 6-Month Preparation Timeline.
Exams.Ninja Tip
With many Oxbridge admissions tests, the older past papers tend to be easier, so working from the older papers to the new ones is a good idea. This will allow you to turn the notch up on the intensity, whilst also sharpening your skills on familiar questions.
Use elimination
In Section 1A, you will find there are 5 potential answers to the question, whereas in Section 1B there are 8. Therefore, using the process of elimination is a lot easier than later on in the paper.
Most ENGAA questions will require 2-step calculations.
Here’s an example:
A metal ball is released from the roof a 20-meter building. Assuming air resistance equals is negligible; calculate the velocity at which the ball hits the ground. [g = 10ms-2 ]
- 5 ms-1
- 10 ms-1
- 15 ms-1
- 20 ms-1
- 25 ms-1
When the ball hits the ground, all of its gravitational potential energy has been converted to kinetic energy. Thus, Ep = Ek:
Exams.Ninja Tip
Remember that to get the correct answer, you must always work in SI units i.e. do your calculations in terms of meters (not centimetres) and kilograms (not grams), etc.
Knowing SI units is extremely useful because they allow you to ‘work out’ equations if you ever forget them e.g. the units for density are kg/m3. Since kg is the SI unit for mass, and m3 is represented by volume –the equation for density must be = Mass/Volume. This can also work the other way, for example, we know that the unit for Pressure is Pascal (Pa). But based on the fact that Pressure = Force/Area, a Pascal must be equivalent to N/m2.
4/5
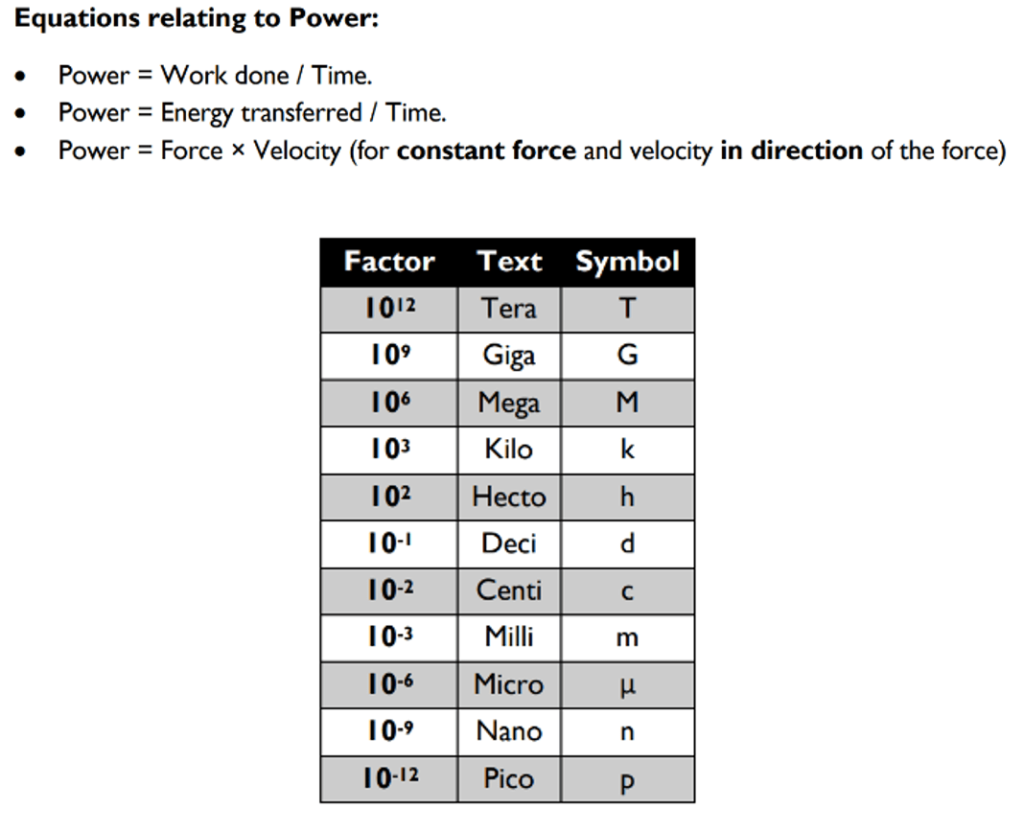
IMPORTANT FORMULAS TO KNOW FOR SECTION 1A
Due to the difficulty of Section 1A as well as its time-constrained nature, it would be a good idea to clear up what formulas you need to know before diving into your revision.



All of the formulas you’ll see below are going to be needed for the physics section of your exam.
Even if questions relating to some of these formulas don’t appear in the paper, you will still need to understand them in order to succeed in your studies as they will come up frequently.
Essential Maths Formulas
Core Geometric Formulas
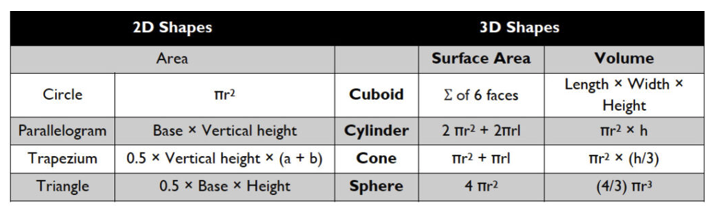

Quadratic Formula
The solutions for a quadratic equation in the form ax² + bx + c = 0 are given by: x = (-b±√(b² – 4ac))/(2a).
Remember, you can use the discriminant to determine how many solutions a quadratic equation has:
b² − 4ac < 0 ⇒ No solutions
b² − 4ac = 0 ⇒ 1 repeated solution
b² − 4ac > 0 ⇒ 2 distinct solutions
Completing the Square
When a quadratic equation can’t be factorised easily and is formatted as ax² + bx + c = 0, then you can rearrange it into the form a(x + b/2a)²[c − b²4a] = 0
In the ENGAA, it’s unlikely that you’ll get a quadratic equation where a > 1 or an equation that doesn’t have easy factors. This gives you an easier equation: (x + b/2)² + [c − b²/4] = 0. Here’s an example:
Consider: x² + 6x + 10 = 0.
We can’t factorise this equation easily but we can note that: x² + 6x − 10 =(x + 3)² − 19 = 0.
Therefore, x = −3 ± √19.
Difference Between Two Squares
If you have to simplify expressions but find that there aren’t any common factors, but the expression does have square numbers, you will sometimes be able to factorise it by finding the difference between the two square:
x² − 25 can also be expressed as (x + 5)(x – 5).
Essential Physics Formulas
Keep these in the back of your mind because you’re going to be using them a lot!
Make the most of your preparation time with the help of Exams.Ninja!
With the Exams.Ninja ENGAA Preparation Platform, you’ll have access to all the resources you’ll need to become an expert in maths and physics. Including tons of guides, practice questions and past papers, Exams.Ninja will guide you all the way through to your exam day!
5/5
ENGAA SECTION 1A PRACTICE QUESTIONS
So now you know what you need to be revising and how to go about it. The next step is to put that knowledge to the test, so here’s a collection of questions to practice your maths and physics skills with! If you don’t know the answer, then you can check out the worked solutions to see how we got the correct answer.
Maths Practice Question 1
Which of the following statements are true about vectors?
A) Vectors can be added or subtracted.
B) All vector quantities have a defined magnitude.
C) All vector quantities have a defined direction.
D) Displacement is an example of a vector quantity.
E) All the above.
F) None of the above.
The correct answer is D.
Vector quantities consist of both direction and magnitude, e.g. velocity, displacement, etc., and can be added by taking account of direction in the sum.
Maths Practice Question 2
Evaluate:


A) 0
B) 25
C) 32
D) 49
E) 56
F) 200
The correct answer is C
Following the rules of BODMAS, the expression can be reduced as shown:
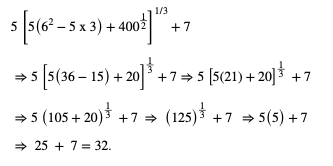
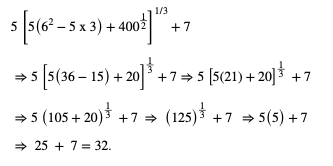
Maths Practice Question 3
S, T, U and V are points on the circumference of a circle, as shown in the diagram, and O is the centre of the circle.
Given that angle SVU = 89°, calculate the size of the smaller angle SOU.
A) 89°
B)91°
C)102°
D)178°
E)182°
F)212°
The correct answer is E
This question tests your knowledge of circle theorems. Angles SVU and STU are opposites and add up to 180° – therefore, STU = 91°.
The angle of the centre of a circle is twice the angle at the circumference – therefore, SOU = 2 x 91° = 182°.



Maths Practice Question 4
An unbiased coin is flipped 4 times. What is the probability of obtaining 2 heads and 2 tails?
A) 1/16
B) 3/16
C) 3/8
D) 9/16
E) None of the above
The correct answer is C
To approach this question, list the six ways of achieving this outcome: HHTT, HTHT, HTTH, TTHH, THTH and THHT. The probability of each of these six outcomes is given by:
1/2 X 1/2 X 1/2 X 1/2 = (1/2)4 = 1/24
Therefore, the probability of two heads and two tails is:
P= 6X 1/24 = 6/16 = 3/8.
Physics Practice Question 1
A battery with an internal resistance of 0.8 Ω and e.m.f of 36 V is used to power a drill with resistance 1 Ω. What is the current in the circuit when the drill is connected to the power supply?
A) 5 A
B)10 A
C) 15 A
D)20 A
E) 25 A
F) 30 A
The correct answer is D.
The total resistance = R + r = 0.8 + 1 = 1.8 Ω and I = e.m.f / total resistance = 36/1.8 = 20A
Physics Practice Question 2
Which of the following statements are correct?
1. Electromagnetic induction occurs when a wire moves relative to a magnet.
2. Electromagnetic induction occurs when a magnetic field changes.
3. An electrical current is generated when a coil rotates in a magnetic field.
A) Only 1
B) Only 2
C) Only 3
D) 1 and 2
E) 2 and 3
F) 1 and 3
G) 1, 2 and 3
The correct answer is G.
Electromagnetic induction is defined by statements 1 and 2. An electrical current is generated when a coil moves in a magnetic field.
Physics Practice Question 3
Which of the following statements is true?
A) When an object is in equilibrium with its surroundings, there is no energy transferred to or from the object and so its temperature remains constant.
B) When an object is in equilibrium with its surroundings, it radiates and absorbs energy at the same rate and so its temperature remains constant.
C) Radiation is faster than convection but slower than conduction.
D) Radiation is faster than conduction but slower than convection.
E) None of the above
The correct answer is B.
When an object is in equilibrium with its surroundings, it radiates and absorbs energy at the same rate and so its temperature remains constant meaning. there is no net energy transfer. Radiation is slower than conduction and convection.
Physics Practice Question 4
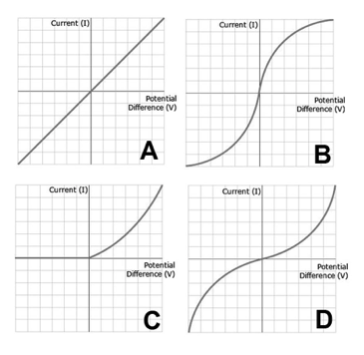
The graphs below show current vs. voltage plots for 4 different electrical components.
Which of the following graphs represents a resistor at constant temperature, and which a filament lamp?
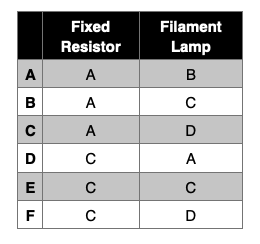

The correct answer is A
For a fixed resistor, the current is directly proportional to the potential difference. For a filament lamp, the metal filament becomes hotter as the current increases. This causes the metal atoms to vibrate and move more, resulting in more collisions with the flow of electrons. This makes it harder for the electrons to move through the lamp and results in increased resistance. Therefore, the graph’s gradient decreases as current increases.
The ENGAA is intended to be a difficult test, as the majority of the applicants score high 8-9 at GCSE. This test is designed to challenge the applicants by getting them to action what they have learned across their study years in an unfamiliar setting. Throughout this article, you’ve learnt the importance of knowing your basics, revising important topics and practicing as much as possible.
Now it’s your turn to get ready for the exam, be sure to make the most of your study time!
Immerse yourself in tutorials, past papers, and an interactive platform to sharpen your skills, so you smash the ENGAA.
Exams.Ninja’s ENGAA Preparation Platform will get you ready enter your exam with confidence and get an immpresive score!
Training Temple- Amazing tips, revision notes and over 100 tutorials to teach you everything you need to know about taking the ENGAA.
Practice Dojo- Over 900 fully worked practice questions, giving you an explanation to every answer you’ll find.
Exam Arena- Attempt 8 actual ENGAA past papers in real exam scenarios. You’ll be able to try them as many times as you want to see how you’re improving.
Start preparing for the ENGAA today to maximise your chances of success.