YOUR ULTIMATE GUIDE
The Definitive Starter Guide To ENGAA Cambridge (2023)
Written by: Matt Amalfitano-Stroud
Please be aware that, as of 2024, the Engineering Admissions Assessment (ENGAA) is no longer being used by the University of Cambridge. Cambridge applicants for Natural Sciences, Engineering, Veterinary Medicine and Chemical Engineering & Biotechnology will be required to sit the Engineering and Science Admissions Test (ESAT).
Welcome to Exams.Ninja’s Definitive ENGAA Starter Guide. This guide is the perfect starting point for your ENGAA preparation, teaching you everything you need to know about the assessment! Here, you’ll find out what the ENGAA is, how it is marked and what you can expect from each section. Plus, you’ll get a chance to try out some ENGAA practice questions to test you skills. Are you ready to get started? We are!
1/4
ENGAA BASICS: EVERYTHING YOU NEED TO KNOW
First things first, let’s cover all of the essential information that you’re going to need to learn before you can even think about sitting the exam! You’ll learn the structure of the ENGAA, how to register, who needs to sit the exam and much more. Let’s jump straight in!


What is the ENGAA and Who Needs to Sit it?
The Engineering Admissions Assessment is a two-hour written exam for those who wish to study Engineering at the University of Cambridge.
The ENGAA is sat on October 18th in 2023 and is one of the most important components of your application alongside your UCAS Personal Statement. You will need to sit the ENGAA before being invited for an in-person interview.
What is the Structure of the ENGAA?
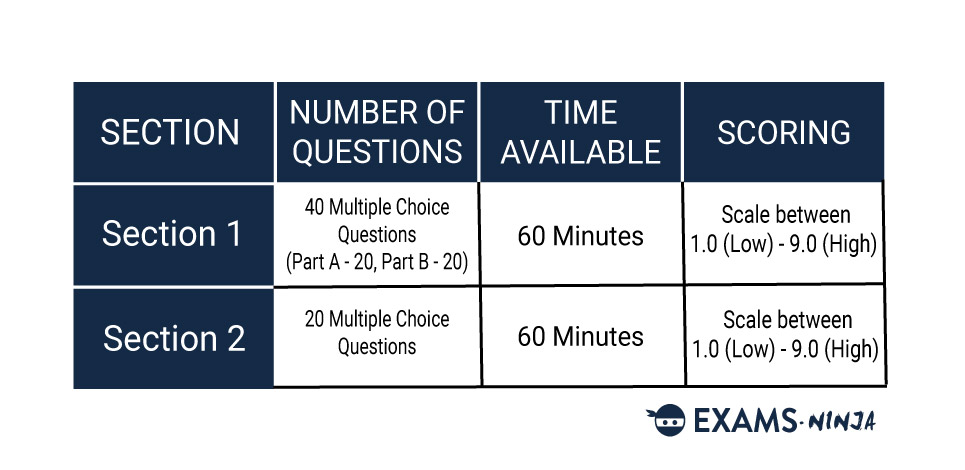
The ENGAA lasts a total of two-hours and is divided into two sections lasting one hour each. Section 1 consists of two sets of questions, labeled as Section 1A and Section 1B. Each question set contains 20 questions to answer. Section 2 contains 20 more questions. Let’s see what each Section contains:
Section 1A contains 20 multiple-choice questions which are centred around Standard difficulty Maths and Physics. Section 1B also contains 20 multiple-choice questions. However, these questions will be based upon Advanced Maths and Advanced Physics, meaning they will be more difficult that Section 1A.
Section 2 contains just 20 multiple-choice questions that are all based upon Advanced Physics. All of the specified knowledge required for this section will be the same as Section 1.
This table summarises the requirements for each section:
ENGAA Structure
Why is the ENGAA used?
The purpose of the ENGAA is to create distinction between Engineering applicants aside from their Personal Statements. Although there is no passing or failing grade, the admissions team will use the final results in conjunction with the rest of the application to determine which applicants should be interviewed.
Although the ENGAA is a major part of you application, a lower score could still be supported by an extremely strong application.
Bear in mind that different colleges within Cambridge with have different weightings and standards for your ENGAA results, so be sure to research your preferred colleges beforehand to see if they have higher standards for your results.
How Much does the ENGAA Cost?
There is no fee required for sitting the ENGAA under regular circumstances. However, a fee may be required if registering with an authorised centre other than your place of education. School leavers should be able to apply directly from their school/college.
How to Register for the ENGAA?
Registration for the ENGAA begins September 1st. If you currently attend school or college, you will first need to speak with the exams officer. They will first inform you of if your place of education is a registered testing centre. If it’s not, you can register for it become one via the Cambridge Assessments Admission Testing website (this process must be completed before September 16th). You may also apply to sit the ENGAA at an alternate testing centre. However, a fee may be required for this.
If your school/college is already registered as a testing centre, your next step is to ask your exams officer to register you for the ENGAA. They will need to be given the following in order to do this for you:
- Personal Details (Name, DOB, etc)
- Your UCAS Number
- The names of the course you intend to apply for
The exam’s officer will then be able to get you registered for the test. You will receive a candidate number once the process is complete, which will be your proof of registration. You must not lose this number as it may be required on testing day. The deadline for registration is September 30th.
If you require a modified paper, you must apply for this by September 16th and must be able to provide medical evidence proving the requirement. Any other access arrangements must be booked by September 30th, alongside the registration deadline.
When and where is the ENGAA sat?
In 2023, the ENGAA testing date has been brought forward and will now be sat on October 18th. You should be able to sit the ENGAA at your school or college. However, if your school isn’t a registered as an ENGAA testing centre or you’re not attending a school or college, you can sit the assessment at an approved test centre.

Key ENGAA Dates
As previously stated, the ENGAA is sat on October 19th, but you need to be aware of the other deadlines and important dates attached to the exam. Let’s take a look:
| Applicants Deadlines 2023 | |
|---|---|
| Registration Opens | 1st September 2023 |
| Modified Papers Registration /Apply to Become a Testing Centre Deadlines | 16th September 2023 |
| Registration Closes | 30th September 2023 |
| Submit Your UCAS Form | 15th October 2023 |
| ENGAA Testing Date | 18th October 2023 |
| ENGAA Results Released | 11th January 2024 |
What do I Need for the ENGAA?
The ENGAA is a written assessment, meaning you will be answering on paper. On the day, you will need take a soft (HB) pencil with you for both sections of the assessment. You will be issued with a separate answer sheet for each section on which to indicate your answers. Do not bring a calculator into the exam.
However, taking a watch with you is always a good idea. Try to bring one that can show you the time in seconds, as this will allow you to have a much more accurate idea of the time you’re spending on a question.
You will also be required to bring a form of ID to the testing centre.
How Hard is the ENGAA?
The ENGAA is by no means an easy test, as it is designed to separate stronger and weaker applicants from each other for the admissions team. While there’s no pass or fail score, you need to aim for the highest score possible in order to strengthen your application and demonstrate your potential as a Cambridge student.
Both sections require knowledge as high as A-Level standards, meaning some more advanced topics are covered. However, the vast majority of what you’ll find here should be covered within your school’s curriculum.
All questions in the ENGAA are multiple-choice, which are typically easier than longer-form questions.
Can I resit the ENGAA?
Students cannot attempt the test twice during the same admissions cycle. If you apply again in another admissions cycle, you must take the test again.
How is the ENGAA Scored?
As a multiple-choice test, your raw mark is equal to the number of questions you got correct. There is no negative marking in the exam, so this value will just be your correct answers. Sections 1A and 1B hold separate scores from each other, along with Section 2.
Your raw marks will then be converted into an ENGAA score, which is measured on a scale between 1.0 and 9.0. Again, each part will be marked separately, but all three are weighed equally.
Below you can see the Score Conversion Table for both sections of the ENGAA in 2021:
ENGAA Score Converstion Table 2021
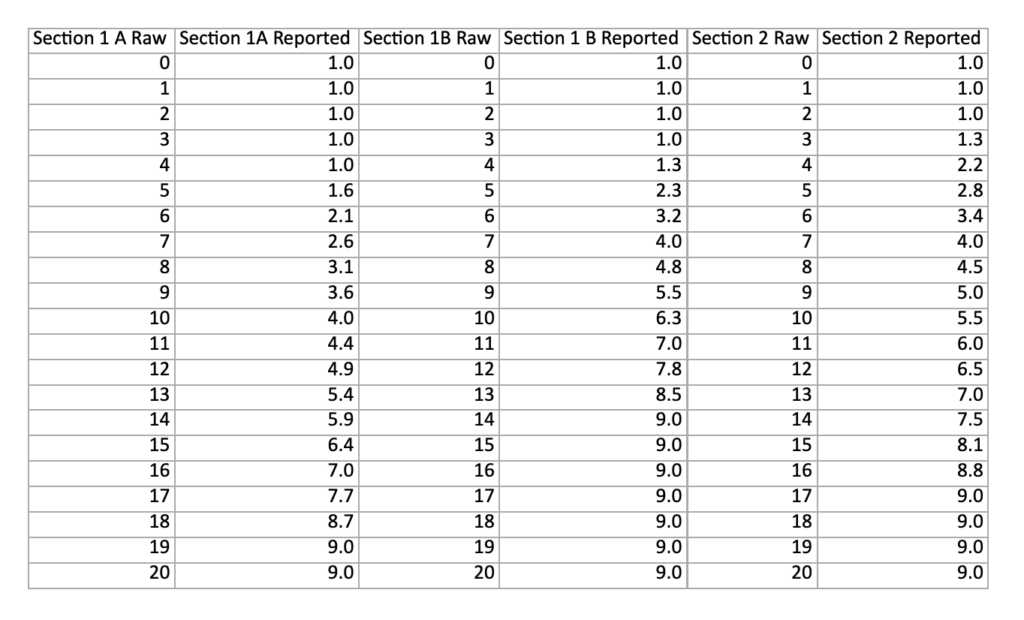

Remember, there is no pass or fail mark for the ENGAA. The test is simply designed for the admissions team to determine your suitability for the course alongside the other components of your application. We have a full guide about Scoring and Results in the ENGAA, so check it out if you want to go deeper into this topic!
Are there any Other Additional Requirements?
Candidates for Gonville & Caius, King’s, Peterhouse, Robinson and Trinity must sit an additional written assessment at interview and mature students (those aged 21 or over) applying to mature colleges don’t take the ENGAA but instead take their own written assessment at interview. Furthermore, some colleges may require STEP as well as ENGAA, so it is a good idea to visit the college’s website for full information as to what you’ll need to do.
There’s no better time to start your ENGAA preparation than now!
Utilise over 900 exam quality questions, each with comprehensive solutions to help you always learn the correct answer. We make sure that the difficulty of the questions matches that of the real exam. Always practice for the real thing. So, why not create and ENGAA.Ninja account and start for free?
2/4
ENGAA SECTION 1A
With the basics out of the way, let’s take a look at the first section of the ENGAA, including it’s layout, specification and practice questions!



Section 1A of the ENGAA is your introduction to the admissions test, and therefore is the easiest portion. All of these questions are based around Standard Mathematics and Physics knwoledge, meaning the majority of topics covered will be at a GCSE level/AS level (or equivalent).
All the questions here are in a multiple-choice format and are all relatively simple. That means you won’t working with a tonne of information/data and will not be worrying too much about real world contexts.
The questions alternate between maths and physics in this section, meaning you’ll regularly be switching between the two. Here’s what a typical ENGAA page will look like when you’re sitting the exam:
ENGAA Section 1A Example Page
Remember that you will be given an answer booklet separately from your question paper, meaning you shouldn’t use the question paper to mark your answers. You can, however, do any rough work on your question paper, as nothing on this will be marked. This will be essential for you to do, as no additional paper is provided for rough work.
ENGAA Section 1A Specification
In order to effectively revise for the ENGAA, you will of course need to know what knowledge is required for the assessment. That’s where the ENGAA Specification comes in! You can find the full ENGAA Specification on the Cambridge website, but here’s a rundown of the specification for Section 1A:
ENGAA Section 1A Maths Specification
- Use Standard Units (time, length, money, etc).
- Use Compound Units (Speed, Density, Pressure, etc).
- Change freely between Standard and Compund Units.
- Apply the four operations (+, -, ×, ÷) to integers, decimals, and fractions.
- Recognise the relationships between operations.
- Use cancelation.
- Apply systematic listing strategies.
- Use Index Laws.
- Understand and apply numbers written in stand index.
- Convert and calculate between decimals, percentages and fractions.
- Calculate with upper and lower bounds.
- Use rounding and approximation.
- Understand and use scale factors, proportion and ratio notation.
- Apply ration to real contexts and problems.
- Work with fractions in ratio problems.
- Solve problems involving percentage change.
- Understand and use direct and inverse proportion.
- Compare lengths, areas and volumes using ratio notation.
- Set up, solve and interpret the answers in growth and decay problems.
- Understand, use and interpret algebraic notation.
- Use index laws in algebra for multiplication and division of integer, fractional, and negative powers.
- Substitute numerical values into formulae and expressions.
- Factorise quadratic expressions in multiple forms.
- Simplify expressions involving sums, products and powers.
- Simplify rational expressions.
- Rearrange formulae to change the subject.
- Work with coordinates in all four quadrants.
- Identify and interpret gradients and intercepts of linear functions ( y = mx + c ) graphically and algebraically.
- Identify and interpret roots, intercepts and turning points of quadratic functions graphically.
- Recognise, sketch and interpret various graphs.
- Set up and solve simple equations including simultaneous equations involving two unknowns.
- Know the quadratic formula.
- Solve linear inequalities in one or two variables.
- Generate terms of a sequence using term-to-term or position-to-term rules.
- Deduce expressions to calculate the nth term of linear or quadratic sequences.
- Use conventional terms and notation.
- Recall and use the properties of angles at a point, angles on a straight line, perpendicular lines and opposite angles at a vertex.
- Understand and use the angle properties.
- Calculate and use the sum of the interior angles.
- Derive and apply the properties and definitions of special types of quadrilaterals and various types of triangles.
- Understand and use the basic congruence criteria for triangles.
- Identify, describe and construct congruent and similar shapes.
- Describe translations as 2-dimensional vectors.
- Know and use the formula for Pythagoras’ theorem (a² + b² = c²) and use in both the 2nd and 3rd dimension.
- Identify and use conventional circle terms.
- Apply the standard circle theorems concerning angles, radii, tangents and chords.
- Solve geometrical problems on 2-dimensional coordinate axes.
- Interpret plans and elevations of 3-dimensional shapes, maps and scale drawings.
- Understand and use three-figure bearings.
- Know various formulae, including the area of a triangle, the volume of a cuboid and the circumference, and area of a circle.
- Calculate arc lengths, angles and areas of sectors of circles.
- Apply the concepts of congruence and similarity in simple figures.
- Know and use the trigonometric ratios.
- Apply addition and subtraction of vectors, multiplication of vectors by a scalar, and diagrammatic and column representations of vectors.
- Use vectors to construct geometric arguments and proofs.
- Interpret and construct various tables, charts and diagrams, including two-way tables, bar charts, pie charts and line charts.
- Interpret and construct diagrams for grouped discrete data and continuous data.
- Calculate the mean, mode, median and range for ungrouped data.
- Describe a population using statistics.
- Make simple comparisons.
- Understand the advantages and disadvantages of summary values.
- Use the median and interquartile range to compare distributions.
- Use and interpret scatter graphs of bivariate data.
- Recognise correlation, and know that it does not indicate causation.
- Draw estimated lines of best fit.
- Interpolate and extrapolate apparent trends whilst knowing the dangers of so doing.
- Analyse the frequency of outcomes of probability experiments using tables and frequency trees.
- Understand and apply ideas of randomness, fairness and equally likely events.
- Relate relative expected frequencies to theoretical probability.
- Apply the property that the probabilities of an exhaustive set of outcomes and mutually exclusive events sum to one.
- Enumerate sets and combinations of sets systematically.
- Construct theoretical possibility spaces for single and combined experiments.
- Calculate and interpret conditional probabilities through representation using expected frequencies with two-way tables, tree diagrams and Venn diagrams.
- Understand the use of tree diagrams.
ENGAA Section 1A Physics Specification
- Know and understand electrostatics.
- Know and recognise the basic circuit symbols and diagrams.
- Understand the difference between alternating current (ac) and direct current (dc).
- Know and understand the difference between conductors and insulators.
- Know and apply the equations for current, resistance, voltage, power and energy transfer.
- Know and understand the use of voltmeters and ammeters.
- Know the properties of NTC (negative temperature coefficient) thermistors, LDRs (light-dependent resistors) and ideal diodes.
- Calculate the total resistance for resistor combinations in series.
- Understand that the total resistance of a parallel combination is less than that of any individual resistor.
- Know and understand the properties of magnets, including their poles, magnetic field pattern and materials.
- Qualitatively understand induced magnetism.
- Know and understand the magnetic effect of a current.
- Know and understand the factors affecting magnetic field strength around a wire.
- Understand the difference between permanent magnets and electromagnets.
- Understand the Motor Effect, including the effects on wire and the application of electromagnets and electromagnetic induction.
- Understand and apply F=BIL for a straight wire at right angles to a uniform magnetic field.
- Know and understand that a voltage is induced when a wire cuts magnetic field lines, or when a magnetic field changes.
- Know the factors affecting the magnitude and direction of an induced voltage.
- Interpret the graphical representation of the output voltage of a simple ac generator.
- Know and understand the terms step-up transformer and step-down transformer.
- Understand power transmission.
- Know and understand kinematics, including scalar and vector quantities, distance–time, displacement–time, speed–time and velocity–time graphs, calculations using gradients and areas under graphs and the equations for speed, velocity, acceleration, average speed and motion.
- Know and understand the different types of forces.
- Know and understand the factors that can affect the magnitude and direction of forces.
- Draw and interpret force diagrams.
- Qualitatively understand resultant force.
- Interpret force–extension graphs.
- Understand elastic and inelastic extension, and elastic limits.
- Know and be able to apply Hooke’s law (F = kx).
- Understand energy stored in a stretched spring.
- Know and understand Newton’s Laws.
- Understand mass as a property that resists change in motion.
- Know and understand the difference between mass and weight, as well as the relationship between them.
- Understand free-fall acceleration.
- Know the factors affecting air resistance.
- Understand terminal velocity and the forces involved.
- Know and be able to use the law of conservation of momentum in calculations in one dimension.
- Know and use the equations for momentum and force.
- Understand work done as a transfer of energy.
- Understand the concepts of useful energy and wasted energy.
- Know and use the equations for work, kinetic energy, power, percentage efficiency and gravitational potential energy.
- Know and understand thermal conductors and insulators.
- Know and be able to apply factors affecting rate of conduction.
- Understand and be able to apply the effect of temperature on density of fluid and fluid flow caused by differences in density.
- Understand thermal radiation as electromagnetic waves in the infrared region.
- Know and be able to apply absorption and emission of radiation.
- Know and be able to apply factors affecting rate of absorption and emission of thermal radiation.
- Understand the effect of energy transferred to or from an object on its temperature.
- Know and apply the equation for specific heat capacity.
- Know the properties and particle models of solids, liquids and gases.
- Be able to compare the densities of solids, liquids and gases.
- Explain pressure and temperature in terms of the behaviour of particles.
- Understand and be able to apply the effect of pressure (P) on gas volume (V) at constant temperature.
- Understand the terms melting point, boiling point, latent heat of fusion and latent heat of vaporisation.
- Know and be able to apply specific latent heat calculations.
- Know and apply the equations for density, pressure and hydrostatic pressure.
- Understand the transfer of energy without net movement of matter.
- Know and understand transverse and longitudinal waves.
- Recall examples of waves, including electromagnetic waves and sound.
- Understand and apply the equations for frequency and wave speed.
- Understand various wave behaviours, including reflection at surface, refraction at boundary and the Doppler effect.
- Draw and interpret ray diagrams to describe reflection in plane mirrors and refraction at a planar boundary.
- Know and be able to interpret angle of incidence and angle of refraction.
- Know and understand the effect of refraction on wave direction (away from or towards the normal) and speed (increasing or decreasing).
- Understand the production of sound waves by a vibrating source and the need for a medium.
- Understand qualitatively the relation of loudness to amplitude and pitch to frequency.
- Understand the cause of echos (reflection).
- Understand longitude waves.
- Know and understand ultrasound and its uses.
- Know and understand the nature and properties of electromagnetic waves.
- Recall the component parts of the spectrum and their order by frequency or wavelength.
- Understand applications and hazards of the component parts of the electromagnetic spectrum.
- Know and understand the terms linked to Atomic Structure, including protons, neurons, electrons, isotope and nuclide.
- Understand the cause of ionisation (loss/gain of electrons).
- Know and be able to apply the nuclear model of atomic structure.
- Know and understand that emissions arise from an unstable nucleus.
- Know and understand the differences between alpha, beta and gamma emission, as well as the nature of each form of radiation.
- Know the deflection and relative penetrating and ionising abilities of alpha, beta and gamma radiation.
- Use and interpret nuclear equations.
- Understand the existence of background radiation.
- Understand the applications and hazards of ionising radiation.
- Interpret graphical representations of radioactive decay.
- Understand the term half–life and use half-life calculators.
Exams.Ninja Tip
Be sure to keep the essential SI prefixes (scientific quantities and units) memorized, as you’ll be using them a lot for the more complex questions.
nano- 10–9
micro- 10–6
milli- 10–3
centi- 10–2
deci- 10–1
kilo- 103
mega- 106
giga- 109
ENGAA Section 1A Practice Questions
Now that we have a better idea of what the questions will look like and what knowledge you’ll need to know for them, it’s time to try out some practice questions:
ENGAA Section 1A Mathematics Practice Question 1
The value of p is directly proportional to the cube root of q. When p = 12, q = 27. Find the value of q when p = 24.
A) 32
B) 64
C) 124
D) 128
E) 216
F) 1728
The correct answer is E.
As p is directly proportional to the cube root of q, we can write the following relation, where k is the constant of proportionality:
p α ∛q ⇒ p = k ∛q
Therefore, we can use the fact that when p = 12, q = 27 to determine the value of k.
12 = k (∛27) = 3k ⇒ k = 4.
Now, at p = 24, we can simply substitute in the values for k and p to determine q:
p = 4 ∛q ⇒ 24 = 4∛q,
∴ 6 = ∛q ⇒ q = 63 = 216
ENGAA Section 1A Mathematics Practice Question 2
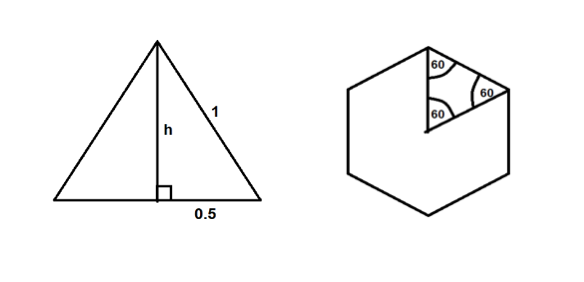
What is the area of a regular hexagon with side length 1?
A) 3√3
B) (3√3)/2
C) √3
D) (√3)/2
E) 6
F) More information needed.
The correct answer is B.
Consider a triangle formed by joining the centre to two adjacent vertices. Six similar triangles can be made around the centre – thus, the central angle is 60 degrees. Since the two lines forming the triangle are of equal length, we have 6 identical equilateral triangles in the hexagon.
Now split the triangle in half and apply Pythagoras’ theorem: 1² = 0.5² + h².
Thus, h = √3/4 = (√3)/2.
Thus, the area of the triangle is: 1/2 bh = (1/2) x 1 x ((√3)/2) = (√3)/4.
Therefore, the area of the hexagon is: ((√3)/4) x 6 = (3√3)/2.
ENGAA Section 1A Physics Practice Question 1
Two identical resistors (Ra and Rb) are connected in a series circuit. Which of the following statements are true?
- The current through both resistors is the same.
- The voltage across both resistors is the same.
- The voltage across the two resistors is given by Ohm’s Law.
A) Only 1
B) Only 2
C) Only 3
D) 1 and 2
E) 2 and 3
F) 1 and 3
G) 1, 2 and 3
H) None of the statements are true
The correct answer is G.
As the two resistors are connected in a series circuit, the current is the same at all points – therefore, statement 1 is true. Due to Ohm’s Law, the potential difference across the two resistors must also be the same – as the current and resistance of each resistor are equal. Therefore, statement 2 is also true. Ohm’s Law can also be applied to the two resistors together, so statement 3 is also correct.
ENGAA Section 1A Physics Practice Question 2
An elevator has a mass of 1,600 kg and is carrying passengers that have a combined mass of 200 kg. A constant frictional force of 4,000 N acts upon the elevator. What force must the motor provide for the elevator to move with an upward acceleration of 1 ms-2? You may assume that g = 10 ms-2.
A) 1,190 N
B) 11,900 N
C) 18,000 N
D) 22,000 N
E) 23,800 N
The correct answer is E.
The total weight of the elevator and the people within it is given by:
W = mg = 10 x (1600 + 200) = 18,000 N.
The total downwards force on the elevator is the sum of the frictional force and the weight. The motor force has to act in the upwards direction. Applying Newton’s second law of motion on the car gives:
FM = Motor Force – [Frictional Force + Weight]
FM = M – 4000 – 18,000 = M – 22,000
The amplitude of a wave is damped from an initial amplitude of 200 to 25 over 12 seconds. How many seconds did it take to reach half its original amplitude? Assume that the wave undergoes exponential decay.
FM = ma = 1800 x 1 = 1800 N
⇒ 1800 N = M – 22,00 ∴ M = 23,800 N.
That covers everything for Section 1A here, but you can learn even more and try out more practice questions in our ENGAA Section 1A Guide!
Advance your skills in maths and physics in time for the ENGAA!
The ENGAA Preparation Programme features tons of resources all available instantly! With over 100+ tutorials and 900+ practice questions, your revision will be taken to the next level! Best of all, you can try it for free now by signing up!
3/4
ENGAA SECTION 1B
Things are getting a bit more advanced now with Section 1B. Everything here is pretty similar to Section 1A, but the questions a much harder now, meaning you’re really going to need to be prepared when testing day comes. Let’s check out what you need to know.



Section 1B is going to look very similar to Section 1A at first glance. The quantity and layout of questions is pretty much identical to what you’ve just seen. However, as we’ve mentioned already, this part of the exam covers Advanced Maths and Advanced Physics.
What exactly makes these questions advanced though? There’s two key factors to consider here really. Firstly , the content knowledge required for these questions is much more advanced, requiring you to have a good understanding of upper A-Level (or equivalent) knowledge to stand a chance here.
This isn’t to say that it’s impossible, as everything covered in the specification here should be taught by your school/college during their curriculum. So the test here is how well you can retain and apply the knowledge you’ve learnt so far.
Secondly, the questions themselves are going to be much more complex. Whereas Section 1A was relatively tame with the amount of information and working out required to solve the problem, the question here will have a lot more depth. You can expect to find additional information/data to work with, real-world contexts to get to grips with and multiple layers of work in order to find the answer you’re looking for.
Getting to grips with all this will require a lot of practice, but let’s first go through the basics, starting with a look at a standard Section 1B page:
ENGAA Section 1A Example Page
ENGAA Section 1A Specification
As with Section 1A, the full ENGAA specification is available publicly to ensure all applicants know what they need to revise. This is a document you should read continuously until you know it page-by-page, but here’s a quick rundown of everything covered for Advanced Maths and Physics:
ENGAA Section 1B Advanced Maths Specification
- Laws of Indices
- Manipulation of Surds
- Quadratic Functions: Graphs, use of discriminant, completing the square
- Solving Simultaneous Equations via Substitution
- Solving Linear and Quadratic Inequalities
- Manipulation of polynomials e.g. expanding brackets, factorising
- Use of Factor Theorem + Remainder Theorem
- Sketching of common functions including lines, quadratics, cubics, trigonometric functions,
logarithmic functions and exponential functions - Manipulation of functions using simple transformations
- Graph of series y=ax
- Graph of y = ax series
- Law of logarithms:
- ab = c <-> b = logac
- logax + logay = loga(xy)
- logax – logay = loga(x/y)
- k logax = loga(xk)
- loga 1/x = – logax
- logaa = 1
- First order and second order derivatives
- Familiarity with notation
- Differentiation of functions like y=xn
- Equations for a circle
- Equations for a straight line
- Circle Properties
- Arithmetic series and Geometric Series
- Summing to a finite and infinite geometric series
- Binomial Expansions
- Factorials
- Solution of trigonometric identities
- Values of sin, cost, tan for 0, 30, 45, 60 and 90 degrees
- Sine, Cosine, Tangent graphs, symmetries, periodicities
- Definite and indefinite integrals for y=xn
- Solving Differential Equations in the form: dy/dx=f(x)
- Understanding of the Fundamental Theorem of Calculus and its application
ENGAA Section 1B Advanced Physics Specification
- Scalars and Vectors
- Manipulating vectors
- Understanding and application of moments
- Understanding both normal and frictional components of contact forces between surfaces
- Applying equilibrium to both stationary particles and those in motion
- Understand and apply the concept of centre of gravity
- Applying equilibrium to rigid bodies
- Using graphical methods to solve kinematic problems e.g. displacement-time graphs
- Solving equations of motion using SUVAT equations e.g. v = u + at
- Using the equation power = force x velocity
- Apply Newton’s laws of motion to point masses under forces
- Solve problems involving projectile motion
- Solve problem involving two bodies connected by a light inextensible, string or rod
- Understand and use the definition of linear momentum
- Understand and use conservation of momentum in 1D problems where bodies collide and coalesce both elastically and inelastically
- Relate conservation of momentum to Newton’s Law i.e. force = rate of change of momentum
- Understand and apply the impulse of a force
- Understand and apply gravitational potential and kinetic energy
- Understand and apply the principle of conservation of energy
- Power = rate of doing work
- Recall and use the equation for efficiency
- Know and apply equations for density and pressure
- Understand and use the concepts of tensile and depressive deformation
- Describe the behaviour springs using terms such as extension and elastic limit
- Apply Hooke’s law to springs and other materials
- Understand the terms stress, strain and ultimate tensile strength
- Know and use the equations for Young’s modulus, stress and strain
- Understand and be able to use the concepts of elastic and plastic deformation
- Describe waves and wave motion using terms such as amplitude, wavelength , frequency, path difference and phase difference
- Recall and use the equations for wave speed and frequency
- Compare and contrast transvers and longitudinal waves
- Understand and apply the principles of superposition and stationary waves
- Identify nodes and antinodes
- Understand and use the concepts of reflection and refraction of waves
- Recall and apply the equation for refractive index
- Understand and use the concepts of critical angles and total internal reflection including relevant equations
- Recall and use equations such as the equations for charge, potential difference, Ohm’s law, power and resistivity
- Understand and interpret the V-I characteristics for different electrical components
- Knowledge of LDRs and NTC thermistors
- Draw and interpret circuit diagrams
- Know and apply Kirchhoff’s Laws
- Solve problems with resistors in series and in parallel including the potential divider circuit
Exams.Ninja Tip
Although calculators aren’t allowed in the ENGAA, there will still be plenty of questions that require moderately complex calculations in order to find the solution.
This is where calculus will become your best friend! It’s not specified in the ENGAA specification, but it’s an invaluable tool to have not only here but throughout your entire academic journey. Our Calculus Guide is in relation to the PAT, Oxford’s dedicated Physics admissions test. However, the major principles within the guide are relevant to any exam, so we would recommend checking it out as a starting point for your revision.
The specification for the ENGAA is nearly identical to that of the Natural Sciences Admission Assessment (NSAA). Both of these exams are operated by Cambridge Assessments Admissions Testing and are used exclusively by Cambridge University. This means that both the standard and advanced Maths and Physics portions of the NSAA specification overlap with the ENGAA. We’ve created a set of guides taking you through everything you need to know about Maths and Physics in the NSAA and the information covered will carry through to the ENGAA. Therefore, we recommend checking them out if you want to go into a more in-depth look at the required knowledge for these two subjects!
Before getting deeper into the content knowledge though, let’s take a look at some more practice questions!
ENGAA Section 1A Practice Questions
It’s time to take a look at some advanced ENGAA questions to get a better understanding of how you can take them on. If you don’t get them right first try, don’t be discouraged! This will likely be the most difficult exam you’ve taken so far so you’re not going to be perfect from day one! If you’re unsure of how these questions are solved, we’ve included worked solutions that fully explain the logic behind the answer.
ENGAA Section 1B Advanced Mathematics Practice Question 1
The area between two concentric circles (shaded) is three times that of the inner circle.
What is the size of the gap?
A) r
B) √2r
C) √3r
D) 2r
E) 3r
F) 4r
The correct answer is A.
The area of the shaded part, that is the difference between the area of the larger and smaller circles, is three times the area of the smaller so: πr² = πx² ⇒ 4r² = x².
∴ x = 2r
The gap, therefore, is given by: x – r = 2r – r = r.
ENGAA Section 1B Advanced Mathematics Practice Question 2
What is the coefficient of the x² term in the binomial expansion of (2 – x)5?
A) -80
B) -48
C) 40
D) 48
E) 80
The correct answer is E.
The binomial equation needs to be utilised here:
(nk)2n-k(-x)k
In this case, n = 5 and k = 2. Therefore, this gives:
⇒ (52)25-2(-x)2 = 10 x 2³x² = 80x².
ENGAA Section 1B Advanced Physics Practice Question 1
The amplitude of a wave is damped from an initial amplitude of 200 to 25 over 12 seconds. How many seconds did it take to reach half its original amplitude? Assume that the wave undergoes exponential decay.
A) 1
B) 2
C) 3
D) 4
E) 6
The correct answer is D.
We can use the proportion of amplitude left to work out how many half-lives, the time taken for the amplitude to half, have passed:
25/200 = 1/8 = 1/2³.
This suggests that 3 half-lives have passed in this duration. Therefore, 12 seconds is three half-lives and t1/2 = 12/3 = 4s.
ENGAA Section 1B Advanced Physics Practice Question 2
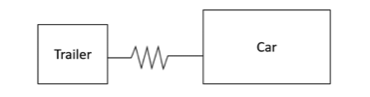
Consider the arrangement below showing a car dragging a trailer using a connection of stiffness 100000 N/m. At an instant they are accelerating at 2 m/s2. Assuming the car weighs 20 Mg and the trailer weighs 10 Mg, what is the energy stored in the spring?
A) 2000 J
B) 2 J
C) 2000 kJ
D) 8000 J
E) 8000 kJ
The correct answer is A.
A free-body diagram on the trailer gives a force exerted by the spring, causing the trailer to accelerate at 2 ms-2. The force is given by:
F = ma = 10,000 × 2 = 20,000 N.
As this is the force exerted by the spring, it is also equal to:
F =kx ⇒ x = F/k = 20,000/100,000 = 0.2 m.
Therefore, the energy stored in the spring is given by:
E = 1/2 kx2 = 1/2 × 100,000 × (0.2)2 = 2000 J.
Be sure to checkout the ENGAA Section 1B Guide for even more information and even more practice questions!
4/4
ENGAA SECTION 2
This is it, the last hurdle between you and ENGAA success! However, ENGAA Section 2 may not be as different as you would think. Let’s find out exactly what you need to know about the concluding section of the ENGAA.
In the past, Section 2 of the ENGAA was actually laid out very differently from the previous section, and many other admissions tests in general. Initially, this section would last only 40 minutes and has an non-fixed amount of questions, usually landing between 15 and 18.
These questions were all focused on Advanced Physics, with no pure maths questions in sight. The key difference with these questions compared to Section 1 was that many of them were linked together by a single scenario. So as an example, Question 1 would actually be made up of three question (A – C), each of which relating to the initial information provided.
In 2019, this format was changed to be in line with Section 1. In the ENGAA you will be taking, you will be given 60 minutes to answer 20 individual multiple choice Advanced Physics questions.
Everything here is now set up basically the same as Section 1, except with the removal of mathematics questions of any form. There’s also the fact that you have the same amount of time to do fewer questions, which is balanced out by the fact that these will be the toughest questions in the exam.
ENGAA Section 2 Example Page
Due to the nature of the questions, there is no additional content knowledge required for Section 2. Everything that you will need to know is covered in the Section 1B Physics Specification, so be sure to go through it again to get a better understanding of what to revise for this Section.
ENGAA Section 2 Tips
As there’s no addition content knowledge to learn for Section 2, let’s instead take a look at a few tips that will help you through the exam. Bear in mind that these tips will also be helpful for Sections 1A and 1B.
You should be aiming for around one mark (or one question) per 2-3 minutes.
Start with the easier questions, these are the ones you’ll know how to tackle immediately. This will build up your confidence and allows you to spend more time on the difficult questions that require more thought.
Practice, practice, practice. Use old exam papers, academic competition papers such as the Physics Olympiad and websites such as Exams.Ninja which contain all previous past papers.
Think in terms of applied formulas, ensure you’re comfortable with all the formulas you need to know and are happy rearranging and manipulating them.
Graph sketching can be difficult, but it can often be used to reach a solution quicker or spot aspects of a problem you wouldn’t have seen otherwise.
We’ve got a full ENGAA Section 2 Guide that details everything you need to know about the second half of the exam. Check it out when you’re ready to learn more about this section of the test!
ENGAA Section 2 Practice Questions
Let’s finish things up with some ENGAA Section 2 Practice Questions! Remember, these will be tough so don’t be afraid to take a look at the worked solution if you’re unsure on how we got the answer!
ENGAA Section 2 Advanced Physics Practice Question 1
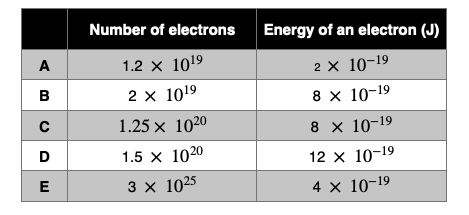
A blue LED has a power output of 10 W, and is connected to a source with an EMF of 5V. Estimate the number of electrons passing through the LED in 10 seconds and the energy provided by the battery to each individual electron.
The correct answer is C.
The current in the circuit can be determined using the power and the EMF. This gives a value of:
P = IV ⇒ I = P/V = 10/5 = 2 A.
This can be used to determine the number of electrons passing through the LED in 10 seconds:
Q = It = 2 x 10 = 20 C ⇒N = 20/(1.6 x 10-19) ≈ (200/16) x 1019 ≈ 1.25 x 1020
The energy of each electron is easily determined using:
W = Vq = 5 x (1.6 x 10-19) = 8 x 10-19 J.
ENGAA Section 2 Advanced Physics Practice Question 2
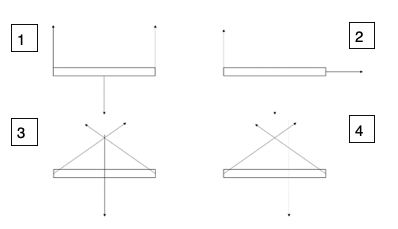
Which of the following beams could not be in equilibrium, regardless of the magnitudes of the forces (assuming they are not zero)? The arrows in the diagrams below represent forces.
A) 1 and 2
B) 1 and 3
C) 2 and 4
D) Only 1
E) Only 4
F) 3 and 4
The correct answer is C.
A body can only be in equilibrium if all the forces are parallel or they all pass through one point, so 1 and 3 fulfil this. Both 2 and 4 cannot be in equilibrium as the balances are not balanced regardless of the magnitude of the forces involved.
ENGAA Section 2 Advanced Physics Practice Question 3
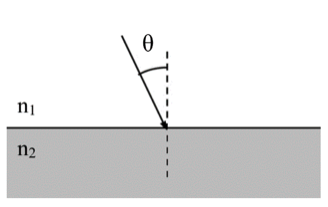
A ray of light is incident upon a surface, as shown in the diagram below. The angle of incidence has been labelled, and the normal is indicated by the dotted line. The refractive index of each material, n1 and n2, is shown in the diagram.
Which of the following statements is true?
A) The light ray will only reflect until the critical angle is reached.
B) If the incident angle is less than the critical value, the ray will undergo total internal reflection.
C) The light ray will only refract until the critical angle is reached.
D) The light ray will reflect and refract until the critical angle is reached.
E) If the incident angle is equal to the critical value, the ray will undergo total internal reflection.
The correct answer is D.
For total internal reflection, the light ray needs to be incident at an angle greater than the critical angle. Statements B and E therefore are false as total internal reflection cannot occur in these cases.
In total internal reflection, all the light is reflected back inside the first medium and none is transmitted to the second medium. For any angle less than the critical angle, we do not get total internal reflection. Instead, there is some reflection back into the original medium and some refraction into the new medium. Therefore, A and C are both incorrect. The light ray partially reflects and refracts until the critical angle is reached.
Therefore, statement D is correct.
ENGAA Section 2 Advanced Physics Practice Question 4
A rock is launched vertically upwards by a catapult and reaches a maximum height of 85 m before starting to fall. Neglecting air resistance and assuming that the rock leaves the catapult when it is 5 m above the ground, what speed is the rock launched at? The acceleration due to gravity is 10 ms-2.
A) 4√10 ms-1
B) 30√2 ms-1
C) 40 ms-1
D) 15√10 ms-1
E) 50 ms-1
The correct answer is C.
As air resistance is neglected, the only components of energy that the ball has are kinetic energy and gravitational potential energy. Conservation of energy states that:
(KEfinal – KEinitial) + (GPEfinal – GPEinitial) = 0
Take the initial state as the point at which the rock leaves the catapult and the final state as the rock’s maximum height, when its speed is zero:
(o – (1/2) mv²) + mg x 85 – mg x5) = 0
The mass of the rock can now be cancelled out:
-(1/2)v² + g(85 -5) = 0 ⇒ 80 x 10 = 1/2 v²
v² = 1600 ⇒ v = 40 ms-1.
If you’re looking for even more practice questions, we’ve got over 900 hundred available at ENGAA.Ninja, alongside our collection of past papers! Sign up today to boost your chances of success!
We’ve gone through a lot here, but you can now say that you have a good understand of the ENGAA! Before you go, here are a few final tips to help with your preparation:
- Start preparing as soon as possible. Like, right after you’ve finished reading this! You’ve already lost two full weeks of preparation due to the exam being sat on October 19th instead of early November, so make the time you have count!
- The exam is only marked positively so don’t be afraid to make an educated guess! Eliminate the options it definitely can’t be, make an educated guess and move on. Your time is valuable!
- Practice as much as you can, it will make you comfortable with the exam and put you at ease. Practicing under exam conditions closer to the time of the test means you can get used to the timings.
- There are no calculators allowed so brush up on your mental math skills.
- Draw quick and simple diagrams where possible, these can help you answer questions and help stop you from making silly mistakes.
- If you’re stuck on a question; pay attention to the options that contain key modifiers like “always”, “only”, “all” as examiners like using them to test if there are any gaps in your knowledge.
Be sure to check out our other ENGAA articles or take a look at ENGAA.Ninja if you want access to the most in-depth ENGAA Preparation Platform available!
Do you want to upgrade your ENGAA revision? Exams.Ninja is just the thing for you!
With the Exams.Ninja ENGAA Preparation Platform, you’ll get to know the exam more intimately than ever before and become an ENGAA genius! When you sign up, you’ll have instant access to these amazing resources:
Training Temple – The home of our essential tips, tricks and tons of expert tutorials (over 100 of them in fact!).
Practice Dojo – The perfect place to practice your skills, with over 900 exam-quality practice questions, each with a full worked solution to boost your understanding of the topic!
Exam Arena – Exams.Ninja has 8 past papers to complete. You’ll get an authentic exam experience alongside an accurate score and worked solutions at the end!
So get ready to maximise your chances of success with Exams.Ninja now!