PAT Guides
PAT Calculus: Everything You Need to Know for the PAT
Written by: Matt Amalfitano-Stroud
The PAT is a tough exam, and calculus is an equally tough subject. Combining the two together therefore is going to be even more difficult, especially considering that other application exams of this nature don’t test calculus to this level. But, it’s not impossible, and we’re here to help you get ready for it! This guide is filled with explanations and examples to help you prepare for any calculus questions that may arise in the test.
1/5
THE BASICS OF CALCULUS AND THE PAT
Here’s a quick rundown of the most basic information you’re going to need to know before you begin your preparation.

What is the PAT?
The Physics Aptitude Test (PAT) is an examination sat by students applying to study Physics, Physics and Philosophy, Engineering Science and Material Science at the University of Oxford. It covers both mathematics and physics and is comprised of multiple-choice questions. You will have two hours to complete the test.
Previously, the PAT required applicants to complete both multiple-choice and written questions, but the latter style was removed in 2024 after Oxford and Pearson VUE formed a new partnership to deliver admissions tests. The PAT is now a computer-based test rather than a paper-based one, so written questions on the level of previous PAT papers would not be possible to replicate on a digital system.
In the PAT, you’ll be provided a digital calculator to use throughout the test. While the calculator only offers basic functions, it’s a great asset to have as very few admissions tests allow the use of a calculator.
What is Calculus?
Calculus (once known as infinitesimal calculus) is the mathematical study of continuous change first developed in 17th-century Europe in its modern form. You’ll be working with two major branches of calculus, differential and integral.
Differential Calculus
As the name suggests, this branch of calculus is all about the differentiation of functions. In its most basic sense, it is the process of finding rates of quantitative change. It has applications outside of pure mathematics, including Physics (in momentum) and Chemistry (in chemical reaction rates).
Intergral Calculus
Again, as stated by its name, this is all about integration. Integrals are used in relation to area, volume, displacement and more. Within Maths and Physics, it can be used to solve problems involving curve lengths, arbitrary shapes and solid volumes, to name a few.
These two disciplines within calculus are both connected by the fundamental theorem of calculus, which states that the two processes are the inverse of each other.
The following three equations are the fundamental rules you must remember that will allow you to differentiate and integrate any polynomial function:
(d/dx)[axn] = anxn-1 (Figure 1)
∫axndx = (axn+1/n + 1) + c (Figure 2)
∫x-1dx = ln(x) + c (Figure 3)
Calculus in the PAT
Specifically for the PAT, there are four major areas of calculus covered in the official exam syllabus:
- Differentiation and integration of polynomials including fractional and negative powers.
- Differentiation to find the slope of a curve, and the location of maxima and minima.
- Integration as the reverse of differentiation and as finding the area under a curve.
- Simplifying integrals by symmetry arguments including use of the properties of even and odd functions (where an even function has f(x) = f(−x), an odd function has f(−x) = −f(x)).
Bear in mind that these are all topics that will be potentially covered in the PAT, but you likely will not encounter all of these within the exam due to the limited number of questions. However, you should still revise your knowledge for all of these as you don’t know what kind of questions may turn up in the actual exam!
It’s also important to note that in previous years (2017 and earlier) there are questions on the PAT that require you to be able to differentiate trigonometric and exponential functions, something that this guide does not cover and is not required for the current PAT syllabus!
It’s time to work out your perfect PAT preparation strategy!
Exams.Ninja’s PAT Preparation Platform is ideal for all stages of your prep, from starting up to the final practice. Start your free demo today to see how you can maximise your score!
2/5
DIFFERENTIATION OF POLYNOMIALS
It’s time to get into the meat of the subject, starting with the differentiation of polynomials.
Differentiation is a process that is used to calculate the gradient (slope) of a function at any given point. We use derivatives to model how a given variable changes with respect to another variable and you will often hear it referred to as the ‘rate of change’.
Unlike a straight line, the gradient of a curve is not constant and so it’s important to be able to find an expression (another function) for that gradient at any given point. The first derivative of a function y = f(x) is notated by either dy/dx or f′(x).
The PAT syllabus only requires you to be able to differentiate polynomial functions and to do this we will use the power rule which is stated below:
(d/dx)xn = nxn – 1 (Figure 4)
Essentially, what we do is bring the power down and subtract by one to obtain the new power. As an example, the derivative of x3 is given by 3x2. We can see the 3 has come down in front of the x and the new power is 2 which is one less than 3. This rule is valid for any n provided it is a real number. This includes negative n and fractional n. Mathematically we say that the power rule is valid for all n ∈ R.
We can also use the power rule when we have a constant factor before our x term. The rule here is to keep the constant there, essentially ignore it! This is stated mathematically as:
(d/dx)axn = anxn – 1 (Figure 5)
As an example let us calculate the derivate of 5x2. Here a = 5 and n = 2 so using the expression above we get 5 • 2x for the derivate or simply 10x.
The final thing you might encounter in a polynomial expression is a constant e.g. the 5 in the quadratic x2+2x+5.
These are really easy to deal with as the derivative of a constant is simply 0 so they disappear entirely! The derivative of the above polynomial is then simply 2x + 2.
Using the equations in Figures 4 and 5, you should be able to differentiate any polynomial expression.
PAT Practice Question 1
What is the derivative of the function f(x) = −7x3 + 22 − x + 1?
A) f′(x) = −14x2 + 4x − 1
B) f′(x) = −21x2 + 4x + 1
C) f′(x) = −21x2 − 4x − 1
D) f′(x) = 14x2 − 4x − 1
The correct answer is C.
PAT Practice Question 2
What is the derivative of the function f(x) = (x2 – 3)2
A) f′(x) = −4x4 – 12x2 + 6x -9
B) f′(x) = (2x – 3)2
C) f′(x) = −4x3 – 12x
D) f′(x) = 2(x2 – 3)
The correct answer is A.
3/5
APPLIED DIFFERENCIALS
In this topic, your knowledge of differentiation is going to be tested in fully applied problems. Let’s take a look at how you can tackle these questions in the exam.
As mentioned earlier, differentiation allows us to find the slope of a curve at any given point. To do this we simply evaluate the expression for the derivative at a given point. Suppose we have the cubic curve y = x3 and we want to know the value of the slope at x = 4. To calculate this we first find the derivative which is dy/dx = 3x2. Then we evaluate this function at x = 4 giving us 3 • 42 = 3 • 16 = 48. So the value of the slope of x3 at x = 4 is 48.
If the value of the slope at a given point is equal to zero, then we call this point a stationary point. These points are important as they tell us where our function is stationary, where it is not changing. Stationary points of a function can sit within one of three categories, they are either a maximum, minimum or point of inflexion.
Maximum and minimum are rather self-explanatory, they are points where the function takes on its greatest or smallest value.
A point of inflexion is a point where a function changes from being convex to concave or vice versa. A good example of this is the point x = 0 on the cubic curve x3, where the curve changes from concave when x < 0 to convex when x > 0.
In order to classify the nature of a stationary point, we need to look at the second derivative (the derivative of the derivative!). To find the second derivate all we do is differentiate the first derivative. The second derivative is notated by d2y/dx2 or f′′(x). From our previous example, we calculated the first derivative of y = x3 to be dy/dx = 3x2. We can easily calculate the second derivative just by differentiating again to get d2/dx2 = 6x.
Imagine we have a function f(x) which has a stationary point at x = a (the value of the first derivative at a is equal to zero). We can calculate the value of the second derivative at x = a (notated by f′′(a)) and use the following three rules to classify it:
f′′(a) > 0 is a minimum point (Figure 6)
f′′(a) < 0 is a maximum point (Figure 7)
f′′(a) = 0 is a point of inflexion (Figure 8)
Exams.Ninja Tip
All the rules and functions that you see in this guide are going to need to be lodged in the back of your brain. memorising all of this is going to take time, so you should spend a bit of time each day reminding yourself of them.
This could be something as simple as writing down each equation once or twice a day until you can do it correctly with no reference! For a more subliminal method, try to leave notes around your room in areas that you look at each day. You’ll have them locked in incredibly quickly!
As an example let us calculate and classify the stationary point of the function f(x) = 2x2 − 4x + 5.
First. we find the first derivative using the power rule which gives us f′(x) = 4x − 4. We know that at a stationary point, the first derivative is equal to zero hence we can set f′(x) = 4x − 4 = 0 and solve for x giving us a stationary point at x = 1.
To classify it we need to look at the second derivate which is simply f′′(x) = 4. Since the second derivate is greater than zero for all values of x, we can conclude that the stationary point at x = 1 must be a minimum point.
PAT Practice Question 3
What is the value of x for which the function f(x) = (x − 3)(x + 1) has a minimum point?
A) x = 1
B) x = −1
C) x = 3
D) x = 0
E) x = −3
The correct answer is A.
To find our minimum point, we first expand and differentiate our function.
f(x) = (x − 3)(x + 1) = x2 + 2x – 3
f’(x) = 2x – 2
Then we set the derivative equal to zero and solve.
f’(x) = 2x – 2 = 0
∴ x = 1
Therefore we have a minimum point at x = 1.
PAT Practice Question 4
(Please be aware that the PAT will no longer feature written questions of this style in 2024. Only Multiple-Choice Questions are included in the test)
Find and classify the stationary point of y = x4 − 32x.
To find the stationary point(s), we take the derivative, set it equal to zero and solve.
dy/dx = 4x3 − 32= 0
4x3 = 32
x3 = 8
x = 2
Therefore we have a stationary point at x = 2.
y(2) = 24 – 32(2)
= 16 – 64
= -48
∴ The coordinates of our stationary point are (2, -48). To classify the point we need to look at the second derivative:
d2/dx2 = 48 > 0 hence this is a minimum point.
4/5
INTEGRATION OF POLYNOMIALS
Let’s flip things over! Next, we’ll be looking at the inverse of differentiation, integration.
Integration is the inverse operation to differentiation. This is the same as how subtracting is the inverse of adding and division is the inverse of multiplication. It is written symbolically as:
if dy/dx = f(x) then y = ∫ f(x)dx (Figure 9)
The dx represents the variable of integration, in this case we are integrating with respect to x just how previously we were differentiating with respect to x. We use integration to find areas bounded by a curve and a coordinate axis or, more simply, we use integration to find the area under a curve.
To integrate polynomial functions we use the inverse power rule which is stated as:
∫xndx = (xn + 1)/(n + 1) + c (Figure 10)
The c at the end is known as the constant of integration. To understand why, it is necessary to think about what happens to constants in the process of differentiation. To verify that this formula is correct, try to differentiate the right-hand side. Remembering that differentiation and integration are inverse operations will often help to simplify many problems! These types of integrals are known as indefinite integrals as they are unbounded.
Figure 7 is not valid for n = −1 (can you see why?). This is a special case that you need to know:
∫x−1dx = ln(x) + c (Figure 11)
where ln(x) is the natural logarithm of x. It is important you understand and memorise this special case.
Integrals that are bounded between two limits are known as definite integrals, these give us the area under the curve. The main difference between indefinite and definite integration is that indefinite integration will result in a function whereas definite integration will result in a numerical value.
The expression below shows how to calculate a definite integrals.
∫ba f′(x)dx = [f(x)]ba = f(b) − f(a) (Figure 12)
We do not require a constant of integration term when evaluating definite integrals.
Exams.Ninja Tip
If you’re more of a visual learner, you can draw out a graph with any integrals you’re working with. The graph won’t need to be to an accurate scale, but having the visual representation may well be what you need to find the answer. Try it out with differentiation as well, it’s equaly useful!
PAT Practice Question 5
What is the area between the curves y = x2 and y = x3 in the interval [0, 1]?
A) 1/3
B) 1/4
C) 1/5
D) 1/12
E) 7/12
The correct answer is D.
Let us first graph these two curves in the given interval.
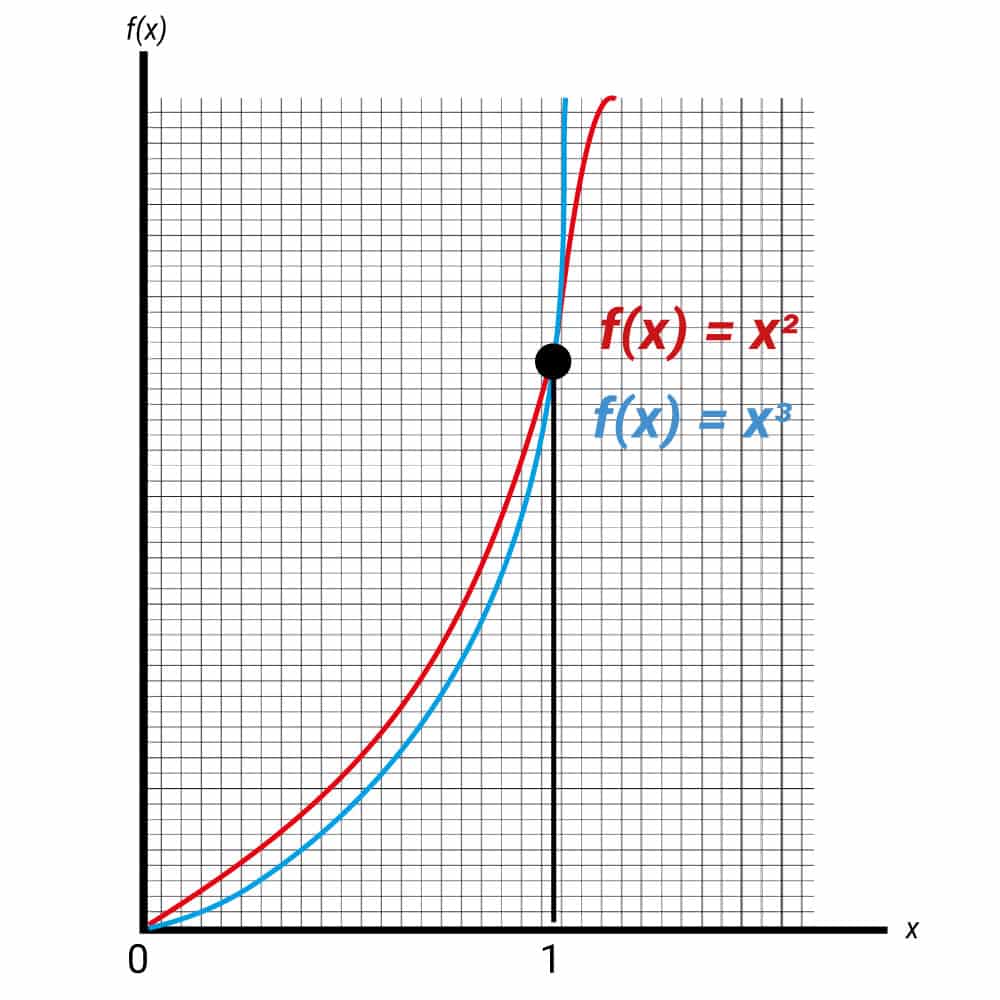
We can see that x2 > x3 in the interval hence the area between the curves will be given by:
Area = ∫1 0 x2dx – ∫ 1 0 x3dx
= [x3/3]1 0 – [x4/4]1 0
= 1/3 – 1/4
= 1/12
PAT Practice Question 6
(Please be aware that the PAT will no longer feature written questions of this style in 2024. Only Multiple-Choice Questions are included in the test)
Given that f′(x) = −2x − x0.5 + 1/3 and g′(x) = f(x) determine the function g(x) such that f(1) = −1 and g(1) = 0.
df/dx = −2x − x0.5 + 1/3
dg/dx = f(x)
Let’s first calculate f(x):
f(x) = ∫(df/dx)dx
= ∫ −2x − x0.5 + 1/3 dx
= –x2 – (2x3/2/3) + x/3 + c
We know that f(1) = -1 and so we can use this to find the value of c.
f(1) = -1 – 2/3 + 1/3 + c = -1
∴ c= 2/3 – 1/3 = 1/3
∴ f(x) = x2 – (2x3/2/3) + x/3 + 1/3
We can now integrate this again to find g(x):
g(x) = ∫(df/dx)dx = ∫f(x)dx
g(x) = ∫x2 – (2x3/2/3) + x/3 + 1/3 dx
g(x) = –x3/3 – 4x5/2/15 + x2/6 + x/3 + c
Again, we know that g(1) = 0, so we can calculate c:
g(1) = -1/3 – 4/15 + 1/6 + 1/3 + c = 0
c = 4/15 – 1/6
c = 8/30 – 5/30 = 3/30 = 1/10
∴ g(x) = x3/3 – 4x5/2/15 + x2/6 + x/3 + 1/10
Looking for more practice PAT questions?
There are over 900 practice questions ready for you instantly with the Exams.Ninja PAT Preparation Platform. You don’t need to be a mathematician to know that’s a lot to get through!
5/5
SIMPLIFYING INTEGRALS USING SYMMETRY PROPERTIES
This is the last major topic that you will need to prepare for the PAT. Let’s see how you can simplify integrals symmetrically.
It is often the case that integrals may be simplified using symmetry arguments. Remembering that the objective of definite integration is to measure the area between a curve and a coordinate axis it is important to note that should the curve go below the coordinate axis, that area is considered ‘negative’. Functions can be classified as even or odd. Even functions have the property that f(x) = f(−x). Some examples of even functions are f(x) = x2 and f(x) = cos(x). This is shown graphically below:
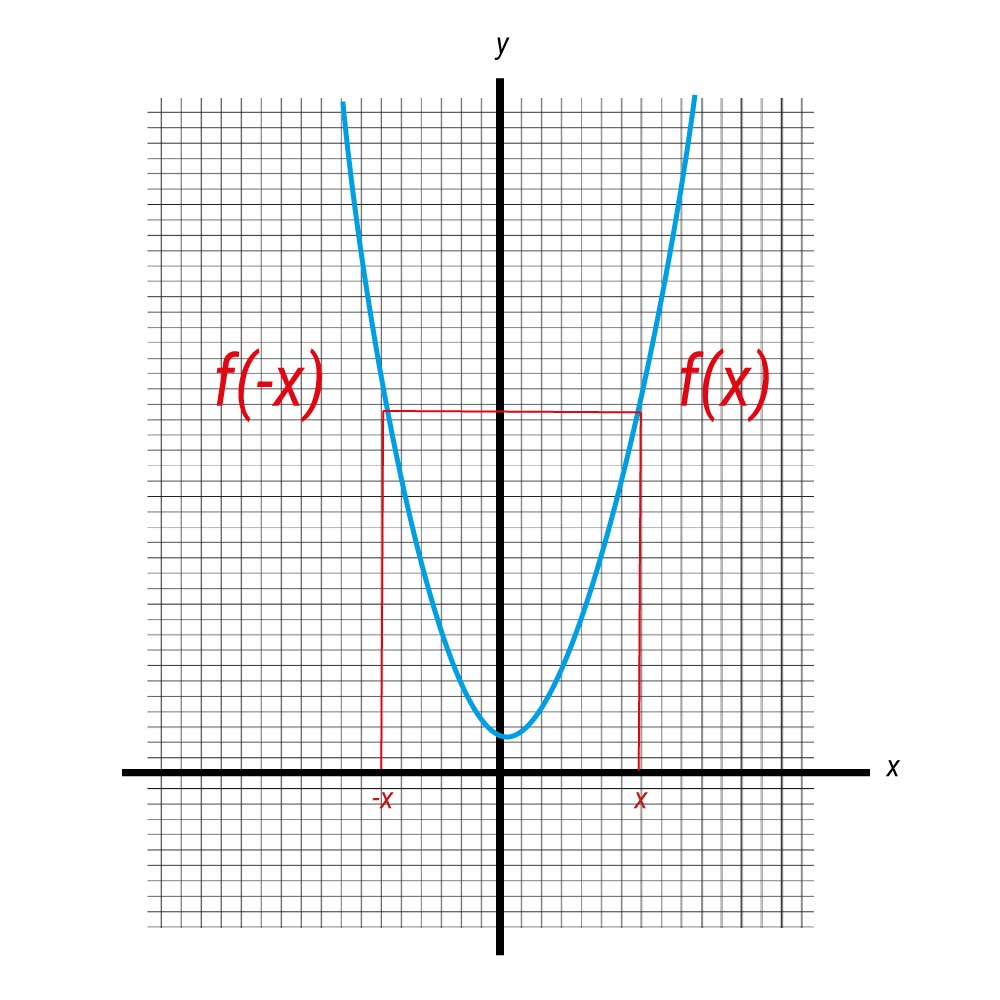
For even functions, if we are integrating over a periodic interval [−a, a] we can simplify the integral as follows:
∫a –a f(x)dx = 2 ∫a 0 f(x)dx (Figure 13)
Odd functions have the property that f(−x) = −f(x). Examples include f(x) = x3 and f(x) = sin(x). Here’s a visual example:
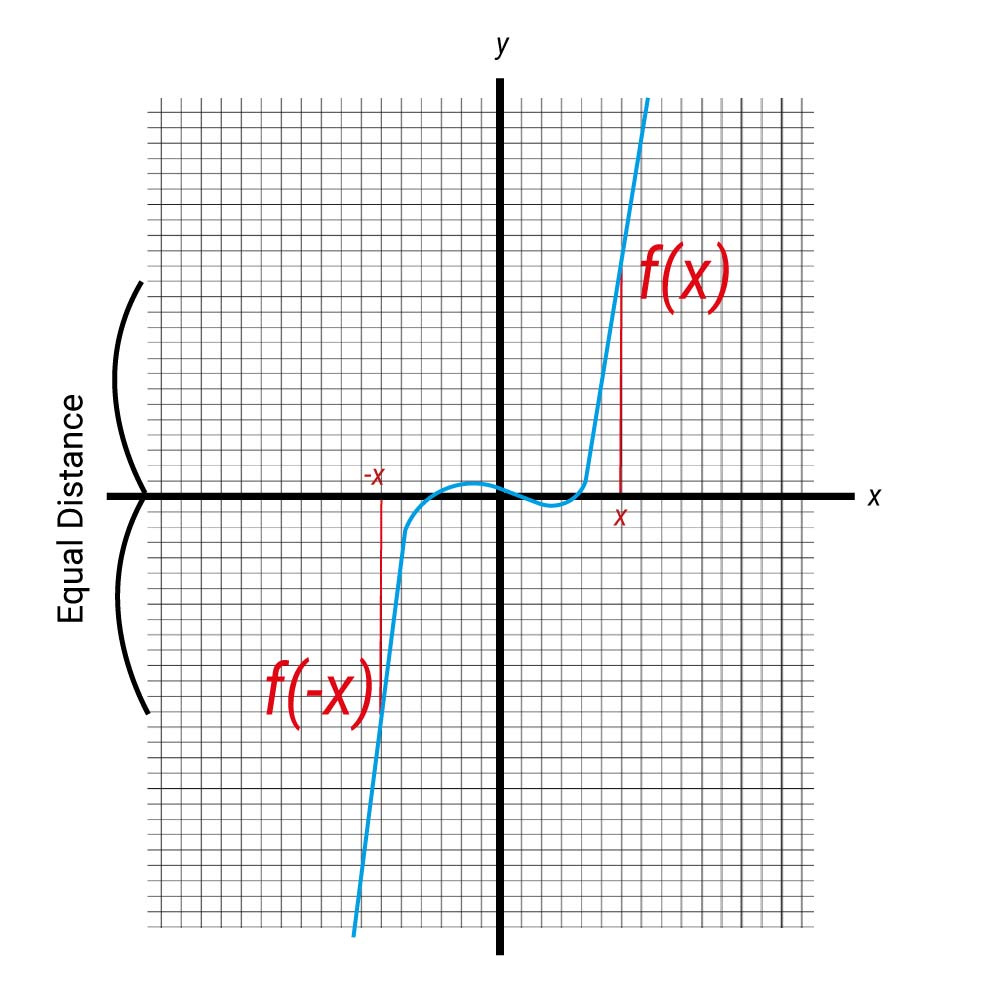
If we are integrating an odd function over a periodic interval [−a, a] then the integral will always be zero:
∫a –a f(x)dx =0 (Figure 14)
This is because the positive and negative areas will cancel out.
PAT Practice Question 7
Determine, without explicit calculation, which of the following integrals are non-zero.
A) ∫3π −3π x2 sin(x)dx
B) ∫∞ −∞ e-x² dx
C) ∫3π/2 −3π/2 cos2(x)dx
D) ∫∞ −∞ xe-x² dx
All the integrals are over a periodic interval and so will only be non-zero if they are even functions (if f(x) = f(-x).
A) contains a sin(x) term and is therefore odd, hence Ia = 0.
B) is the Gaussian Kernel and because x² = (-x)². This is even, hence Ib ≠ 0.
C) contains a cos(x) term and is therefore even, hence Ix ≠ 0.
D) contains an x term and since x ≠ –x. This function is odd, therefore Id = 0.
Therefore, options B) and C) are non-zero.
PAT Practice Question 8
(Please be aware that the PAT will no longer feature written questions of this style in 2024. Only Multiple-Choice Questions are included in the test)
Determine if the function x/(x²−1) is even, odd or neither.
To see if the function x/(x²−1) is odd or even, we can substitute –x and see what happens:
f(-x) = –x/((-x)²−1) = x/(x²−1)
f(-x) = f(x)
Hence, this is an odd function.
The calculus questions in the PAT can seem intimidating. However, remembering the rules for performing differentiation and integration will ensure you have the skills to answer any questions. The most effective way to revise for the PAT is to do as many practice questions and past papers as possible! If you want to learn how to plan out your revision to make the most use of your time, check out our PAT 6-Month Preparation Timeline!
Alternatively, If you want to learn more about the PAT as a whole, check out our Definitive PAT Guide!
Are you still calculating the most effective PAT revision plan? Exams.Ninja’s got you covered!
There’s a lot to prepare yourself for in the PAT, but you’ll be able to get through it easily with Exams.Ninja’s PAT Preparation Platform! There are tons of features and content available to you, including:
Training Temple- You’ll have instant access to over 100 expert tutorials, along with loads of helpful revision notes and tips.
Practice Dojo- Sink your teeth into over 900 practice questions, all based on the topics you’ll need to know for the test. Then confirm your knowledge with a fully worked solution for each question you try.
Exam Arena- We have 5 full past papers from the PAT available for you to try out. See how you’ll perform on the big day by practising in realistic exam conditions and get an accurate score at the end!
Start your PAT prep today and boost your chances of success!

