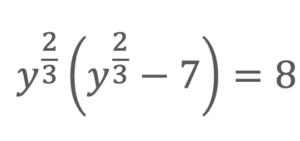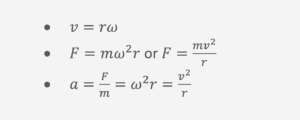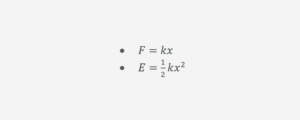YOUR ULTIMATE GUIDE

The Definitive Starter Guide To The PAT Oxford (2024)

Written by: Matt Amalfitano-Stroud

In this definitive guide we are going to go through all of the information that you’ll need to know to get prepared for PAT Oxford! At first, it can seem a bit intimidating with the focus on problem solving than knowledge about a topic, but proper preparation will soon get you accustomed to test. We’ll go through the essential test information, the different question types and plenty of practice questions that should give you an idea of what to expect.

1/3

PAT BASICS: EVERYTHING YOU NEED TO KNOW

Before you start your PAT preparation, let’s look at some important information about the exam. You’ll learn what the PAT is, why Unis use it, who who need to sit the exam and more. Let’s get started:

What is the PAT Oxford?

The PAT Oxford (Physics Admissions Test) is a pre-interview computer-based test that is used by the University of Oxford during the selection process of various science-based courses. As of 2024, the PAT will be delivered by Pearson VUE.

What is the Structure of the PAT Oxford?

The PAT is an incredibly basic admissions test format-wise. The whole exam is made up of just one section comprised entirely of multiple-choice questions.

The PAT was previously a paper-based admissions test delivered by Oxford itself. The test had a very loose structure with varying question totals from year to year and three different styles of questions; multiple-choice, written and multi-part. The latter two were worth multiple marks and required applicants to write out both their solution and process to earn full marks.

However, in 2024, Oxford partnered with Pearson VUE to deliver all of its university admissions tests, including the PAT. Pearson VUE specialises in computer-based testing, so all Oxford admissions tests were moved to their dedicated testing system.

The written/multi-part questions of the PAT required more complex solutions with advanced mathematics notation, so these were not possible to translate into a digital format. As a solution, the format of the PAT was changed to only include multiple-choice questions.

Currently, we don’t know how many questions will be included on the test.

TSA Oxford Structure

Why is the PAT Oxford used?

Different admissions tutors, and different subjects will use the PAT in different ways post-interview – so there is no definitive rule for what score you need to be aiming for to get an offer. The main aim of the PAT is to take the number of applicants applying (in 2019 there were 8.8 applicants per place in physics), and narrow it down to a more reasonable 2.5 applicants per place who will be offered an interview.

In this shortlisting process the PAT is the single most important part of your application. Up until 2019, GCSEs weren’t even used, it was just the PAT test! However, there isn’t a passing or failing score in the PAT, so a lower score can still be supported by a very strong application.

How Much does the PAT Oxford Cost?

Nothing! There is no fee required for sitting the PAT Oxford under regular circumstances.

How to Register for the PAT Oxford

Applicants for the PAT will need to register through Pearson VUE’s online portal. You can create your Pearson VUE account as early as May, but bookings for the PAT don’t open until August 15th. When creating an account, you’ll need to provide various personal and contact details.

When bookings open, you’ll first be required to confirm the test you’re taking. Then you’ll need to select the testing centre you wish to attend and choose a testing date and time slot based on the centre’s availability. Once you’ve submitted your booking, you’ll receive a confirmation email with your testing slot details.

We suggest booking your test as early as possible to ensure you get the tie slot you want.

When and where is the PAT Oxford sat?

In 2024, the PAT Oxford can be sat on October 28th. You will be required to sit the PAT at a Pearson VUE testing centre. These are located all across the globe, including over 100 within the UK.

Key PAT Oxford Dates

We’ve seen previously that the PAT Oxford is sat on October 28th. However, you also need to be aware of the other deadlines and important dates attached to the exam. Let’s take a look 2024’s key dates:

Applicants Deadlines 2023
Registration Opens	15th August 2024
Registration Closes	4th October 2024
Submit Your UCAS Form	15th October 2024
PAT Testing Date	28th October 2024
PAT Results Released	November 2024

But when should you start preparing? We would recommend starting 6-Months in advance! You can see how we suggest you use your time with our PAT Preparation Timeline.

Who has to sit the PAT Oxford?

Remember that this exam is exclusive to Oxford, and is a requirement for all applicants of the following courses:

PAT Oxford Courses

What do I Need for the PAT?

The PAT is a computer-based test, meaning you won’t be answering on paper. However, you should still receive paper for working out, so you will need to bring a soft (HB) pencil. A digital calculator is included on the digital testing system, so no additional resources are required or permitted.

Taking a watch with you is always a good idea, especially one that can show you the time in seconds. This will allow you to have a much more accurate idea of the time you’re spending on a question.

You will also be required to bring a form of ID to the testing centre.

How Hard is the PAT Oxford?

All the content is carefully designed to ensure it’s at the standard you’ll already be working at, so you don’t need to do a lot of extra work or teach yourself anything new just for your application.

One thing worth noting is that your school may not be teaching maths and physics in the exact order that Oxford expect you to be taught them. This means you do need to work through the official syllabus to make sure that you have seen everything and picked up any bits that you haven’t learnt at school yet (PAT.Ninja is the perfect platform for this).

The main thing to remember when looking at the syllabus is that knowing the content is only half the challenge. What sets the PAT apart (and makes it more useful to the admissions tutors than just looking at your GCSE and mock results) is the way it asks you to apply the content in new or unusual contexts. This is why practising with questions and past papers is so important as part of your preparation.

Can I resit the PAT Oxford?

Students cannot attempt the test twice during the same admissions cycle. If you apply again in another admissions cycle, you must take the test again.

How is the PAT scored?

Since the PAT has changed to only include multiple-choice questions, the scoring system will be based on how many questions you answer correctly. We currently don’t know if scores will be converted in any way, but the system may be similar to the system used previously.

The raw mark of the exam was converted into a percentage which acted as your final result. Your result will not be automatically sent to you after the exam. Instead you will need to request for it to be sent to you via the university’s Feedback process. There’s far more to it than this though, so be sure to check out our PAT Results and Scoring Guide!

The PAT is a difficult test, so build your skills up with PAT.Ninja!

PAT.Ninja is the world’s best PAT Preparation Platform that provides you with everything you need to prepare for the big test. Give it a try today by signing up for free!

2/3

PAT MATHEMATICS

Let’s take a look at the first of the two types of questions you can expect in the PAT; Mathematics. We’ll see what the questions look like, what you’re going to need to revise and finish off with a selection of practice questions!

There isn’t an official first section to the PAT, but we feel that maths is the best place to begin your PAT revision. Let’s start things off by taking a look at how you can expect the questions to look on the actual PAT paper:

PAT Maths Example Question

There’s nothing too out of the ordinary here if you’ve ever taken a maths exam before. You’ll be answering the questions digitally so your working out won’t be marked. However, you may be able to request paper to complete rough work on during the test.

PAT Mathematics Syllabus

As we mentioned earlier, the purpose of the PAT is not just to test your maths and physics knowledge – if it was, they wouldn’t be getting any information that your A-level or IB exams couldn’t give them. That being said, the knowledge is obviously an important part of doing well, so let’s take a look at the stuff you’re going to need to know!

Elementary Mathematics

This is all the stuff you did at GCSE (or equivalent) level. Don’t assume that just because you’ve moved onto bigger and better things that it can all be forgotten! The official syllabus mentions arithmetic (mental maths and the ‘numbers’ topics in most exam specifications), geometry and coordinate geometry, as well as probability – so make sure to prioritise these, but if you get a chance, revise it all!

For most students this generally means going back and revising loads of geometry which they haven’t seen in nearly two years – don’t let the easy stuff catch you out! Although none of this is likely to be a standalone question, there are often steps in bigger questions which rely on you being able to use geometrical relations or find probabilities at the drop of a hat – if you can’t remember the rules it can stop you dead in your tracks.

Take a look at the following questions – could you answer them?

How would you work out the interior angles in an n-sided polygon?
What’s the equation for area of a trapezium?
What does the alternate segment theorem say? Could you spot it in a question?
If I want to find the probability of one event AND another event happening, how does that differ from the probability of one event OR the other? What happens if the events aren’t mutually exclusive?
- If you’re stuck on probability questions remember that the old method of drawing 2-way tables or tree diagrams is helpful for visualising what’s going on.
When looking at a block on an inclined plane – why is the parallel component of the weight found using sin(x)? Can you show this convincingly?

The other part of elementary mathematics which is often overlooked is your mental maths ability. While it’s not important in the PAT as in other aptitude tests which don’t have a calculator (good choice!), your ability to estimate and, as a result, spot ‘silly’ calculation errors is so important in making every mark count. It’s also really helpful if you’re trying to factorise slightly awkward quadratics quickly.

Algebra

There’s a lot to cover here so let’s split everything into categories:

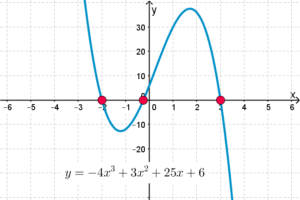
Polynomials

You need to be able to solve quadratics by factorising, by completing the square, and by using the quadratic formula.

If you’re asked for an exact value make sure you keep your answer in terms of surds, and don’t calculate decimals of irrational numbers – they’re not ‘exact’.
If you can skip solving the entire question by just using or similar to find the information you need and nothing else – you should always cut whatever corners you can!
For many students it’s worth looking ahead at the factor theorem (and the remainder theorem) if you haven’t seen them, as they can really speed up your ability to find solutions to equations larger than quadratics. ‘Common sense’ approaches, like finding the factors of the ‘constant’ value at the end of the equation to inform the values you true, are also good to practice.

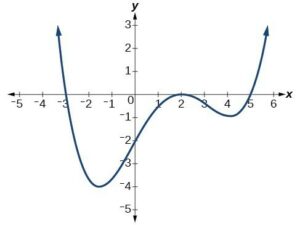
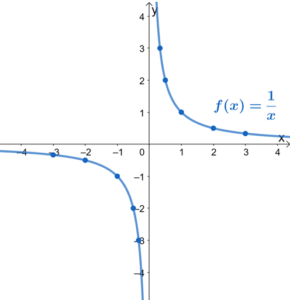
Graph Sketching

You need to know the shapes of common graphs, and how to sketch versions of these graphs which have been transformed. The main graphs you should know without calculation are:

Polynomial Graphs

Reciprocals

Roots

Exponentials and logarithms

Trigonometry

Sin(x), cos(x), tan(x) – don’t worry about any other trig you may have learnt about beyond this.

You need to know the shapes of common graphs, and how to sketch versions of these graphs which have been transformed. The main graphs you should know without calculation are polynomial graphs, reciprocals, roots, exponentials

You should also be able to use differentiating and setting equal to zero to find stationary points, and differentiating a second time to find the ‘nature’ of the stationary point (i.e. Whether it’s a maxima, minima, or point of inflection).

One of the main ways graph sketching can be complicated is by writing the expression in an unusual format – make sure you remember your GCSE techniques for dealing with this.
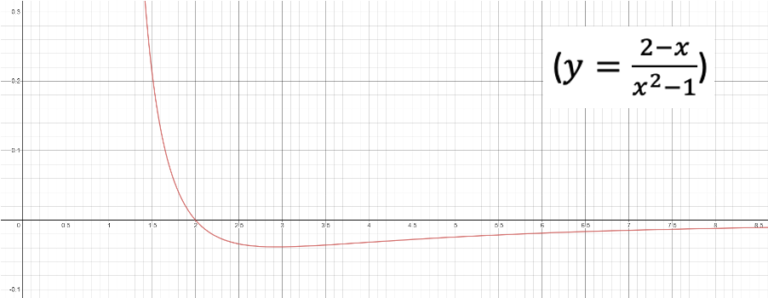
Make sure you know how asymptotes work. Although they’re often (incorrectly) defined as ‘lines which a curve tends toward but never meets or crosses, this is not strictly true, which causes issues for some students. The graph below has an asymptote along the x-axis, and yet it crosses it at x=2, prior to tending back towards y=0 as it tends to infinity.

Transformation of Variables

‘Transformations’ are hopefully quite familiar in times of graphs, but do make sure to revise translations, expansions, and reflections (and how they differ in the ‘x’ and ‘y’ direction). These are more likely to arise in questions where you’re not told the actual function ‘f(x)’, but given a graph with a minimum or maximum point labelled, and asked to figure out where that point will be on a transformed version.

This is not the only meaning of ‘transformation’ though. You may also be asked to transform variables in order to make an equation easier to solve. Some of you may already have seen ‘integration by substitution’ which is an example of the benefits of this. For everyone else, transformation of variables is probably most familiar from ‘quadratics in disguise’ at GCSE. It’s pretty tricky to figure out where to start, when figuring out the solutions to the equation below, without substituting in another variable to help solve it – have a go!

Solutions to Inequalities

The good thing about inequalities is that by the time you’ve made it to the PAT you’ve finally escaped from ‘draw the following inequality on a number line’ questions! You do need to be able to solve inequalities though, including ones which contain quadratics.

If you’re solving a quadratic inequality always draw a graph – it takes 2 seconds to draw a rough sketch, and it’s not worth risking losing the marks by trying to hold it all in your head. (In fact, if we could have a single mantra for every maths and physics exam you ever sit it would be draw a diagram!).
Remember that if you multiply or divide by a negative number you must change the direction of the inequality sign.
- This is why you should never multiply or divide by ‘x’ (or whichever variable you’re using) in these questions – what if one of the values of ‘x’ is negative and you don’t know? Factorise out if you need to, but if you divide before you know what ‘x’ is you’re risking ending up with the inequality sign completely backwards.
Always combine inequalities as early as you can. The easiest way to do this is often to sketch a number line rather than trying to hold all the equations in your head (you can’t completely escape them).

Elementary Trigonometry

Trig in the PAT is all stuff you’ve been doing for a while now. A lot of students will have recently learnt about a whole load of more complicated trigonometry such as expressing sin(A+B) in terms of sin and cos, or the definitions of new expressions such as secant, cosecant, and cotangent (?!?!). The good thing about the PAT is that you can forget all of this! You need to know your ‘SOHCAHTOA’, and how you link sin, cos, and tan, as well as the trig identity for the squares of sine and cosine. And that’s it! None of the new stuff!

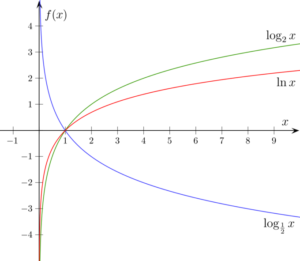
Logarithms and Exponentials

You should know what exponentials and logarithms are, and how they relate to each other in solving equations. You must also know your ‘log laws’, including how to change the base of a logarithm, this is something which is not included in most A-level specifications but does come up on the PAT occasionally – so make sure you know how to do it.

Sequence and Series

Make sure to familiarise yourself with the definitions (and nth-term formulae) for both geometric and arithmetic sequences and series.

You won’t be provided with the equations for the sum to n terms, or the sum to infinity of sequences and series, so if you’re used to looking them up on the formula sheet in your other exams, you must memorise them for the PAT (sorry!)
You should also be aware that you may need to spot sequences in unfamiliar contexts (for example, let’s say you have a spring oscillating around an equilibrium position, and it’s dissipating a set percentage of kinetic energy each time it oscillates – it’s kinetic energy will form a geometric series, and this may be the way to solve the question. Remember what we said earlier about ‘maths’ techniques cropping up to simplify ‘physics’ questions!).

Binomial Expansions

This is probably the bit that people most struggle with in the entire specification. Fortunately it doesn’t come up in questions that often.

You should, however, make sure that you could expand something like (2 + 3x)^7;
You should also bear in mind that it may be easier to ‘expand’ brackets (or combine them) prior to using a binomial expansion. For example, in this question – which can easily take much longer than it needs to if you don’t spot the ‘trick’- what is the coefficient of x^3 in the expansion of (1 – 2x)^5(1 + 2x)^5 ;

Calculus

We have a full guide on Calculus in the PAT available to read when you’re ready to go more in depth. However, let’s first take a quick look at the topic:

Differentiation and Integration

Make sure you know how to calculate all of the following:

Differentiate and Integrate:

Integrate:

Other rules about calculus ‘in practice’ which you will hopefully be familiar with already:

Integration is the reverse of differentiation (as a hint – this means if you’re told how to differentiate something unfamiliar, then you can figure out how to integrate by running the instructions in reverse. E.g. ‘multiply by the differential, multiply by the power, reduce the power by one’ becomes ‘add one to the power, divide by the power, divide by the differential);
You can find the slope of a curve, the location of turning points, and the nature of turning points using differentiation (make sure you know how to do this);
You can find the area under a curve using integration;
You can simplify integration by noticing areas which ‘cancel’ each other out as they’re odd or even functions.
A clear graphical understanding of integration (and what the limits represent) is essential for questions like this one:

That’s quite a lot to remember in one go, which is why it’s so important to revise consistently throughout the entire time from now until testing day. Don’t forget to read through the Official PAT Syllabus regularly, this is what you need to base your revision around.

Before we move on to physics, why don’t we try out a few PAT Practice Questions for Mathematics:

PAT Mathematics Practice Questions

PAT Mathematics Practice Question 1

If x = 1 is a root of the equation 2x³ + x² – 5x = -2, find the other two roots. [2]

A) x = 1 and x = 2

B) x = 1/2 and x = 2

C) x = 1/2 and x = 1

D) x = 1/2 and x = -2

E) x = -1/2 and x = -2

The correct answer is D.

If x = 1 is a root, then (x − 1) is a factor. If we factorise (x − 1) out of the polynomial we get: 2x³ + x² − 5x = −2

2x³ + x² − 5x + 2 = 0

(x − 1)(2x² + 3x − 2) = 0

(x − 1)(2x − 1)(x + 2) = 0

Hence, the other two roots are x =12 and x = −2.

PAT Mathematics Practice Question 2

How many numbers greater than 3000 may be formed by using some or all of the digits 1, 2, 3, 4, and 5 without repetition? [2]

A) 144

B) 160

C) 176

D) 188

E) 192

The correct answer is E.

We can see that the numbers must be either 5 digits, when any combination is valid, or 4 digits, when the number must start with either 3, 4 or 5.

There are therefore 5 × 4 × 3 × 2 × 1 = 120 possible 5-digit options, and 3 × 4 × 3 × 2 = 72 4-digit options.

In total there are therefore 120 + 72 = 192 combinations

PAT Mathematics Practice Question 3

(Please be aware that the PAT will no longer feature written questions of this style in 2024. Only Multiple-Choice Questions are included in the test)

Expand (5 – 3x)⁴ as a sum of powers of x. [5]

Answer:

Using binomial expansion,

(5 − 3x)4 = (5)4 + 4(5)3(−3x) + 6(5)2(−3x)2 + 4(5)(−3x)3 + (−3x)4

=625 – 1500x + 1350x² – 540x³ + 81x⁴

PAT Mathematics Practice Question 4

(Please be aware that the PAT will no longer feature written questions of this style in 2024. Only Multiple-Choice Questions are included in the test)

For 0 ≤ x ≤ 2π, what is the solution for the following equations? [6]

A) sin x cos x = 1/2

b) sin² x – cos² x = 0

Answers:

a) Using the sin 2x identity,

sin x cos x = 12

sin 2x/2 = 12

sin 2x = 1

2x = π/2, 5π/2

x = π/4, 5π/4

b) Using the cos 2x identity,

sin² x – cos² x = 0

–cos² x = 0

cos² x = 0

2x = π/2, 3π/2, 5π/2, 7π/2

x = π/4, 3π/4, 5π/4, 7π/4

Need support with your PAT Prep? PAT.Ninja is exactly what you’re looking for!

Access over 100 tutorials, 900 practice questions and 5 past papers in realistic exam conditions sounds, all when you upgrade your PAT.Ninja account. Create your free account today and start your preparation!

3/3

PAT PHYSICS

If you’re taking this admissions test, you’re going to be apply for to study Physics at Oxford, so this part of the test is going to be pretty important! Let’s go over what you’re going to need to get a great score!

Physics is probably the portion of this exam that you’re more invested in, you are hoping to study a physics-heavy subject after all! The questions aren’t laid out any differently from the maths ones, but let’s take a look at some examples anyway:

PAT Physics Example Question

As you can see, they’re a bit longer than the maths questions, most likely because of the amount of diagrams you’ll find. Other than this though, there’s not really any major differences to note, so be sure to follow the same rules that we stated for the maths questions.

PAT Physics Syllabus

Now it’s time to head back to the PAT Syllabus to check out what you need to know for physics. The Official PAT Syllabus isn’t massive compared to some other admissions test, but it’s still definitely essential to read through.

For now though, let’s run through everything that’s stated in it, along with a bit of extra context:

Mechanics

This is definitely one of the bulkier parts of Physics, covering everything from forces to energy. Here are the major subjects highlighted in the PAT Syllabus:

Distance, Speed, Velocity, and Acceleration.

You must understand the difference between scalars and vectors, and be able to use that when dealing with the relationship between speed and velocity, or when considering velocity as the rate of change of displacement, etc…

You also need to memorise your SUVAT equations and be able to spot the situations in which they’d be inappropriate to use.

It’s almost always best to start any SUVAT question by drawing a diagram in which you define which direction is positive, and which is negative. It’s so easy to make arithmetic mistakes on otherwise straightforward questions if you don’t!
You may also need to go back and revise the graphs of velocity, acceleration, and displacement which you looked at during GCSE. What is the area under a velocity-time graph? What about the gradient?
- This may be developed further in situations which wouldn’t suit SUVAT equations, for example, if you were given an expression for velocity in terms of time and asked to find acceleration, you would need to find rate of change by differentiating.

Newton's Laws of Motion

You need to know how to use (not how to quote) the 3 laws of motion, you should be able to convert between weight and mass using ‘g’ (which you can approximate to 10 in some questions, so always double check on a case-by case basis).

Circular Motion

You should know the following circular motion equations:

Common Forces

You should know what friction is (but don’t worry about anything you may have done about ‘coefficients of friction’ in maths for the PAT), you should know about air resistance, and the fact it’s proportional to the square of the velocity. The fact that air resistance is proportional to a function of velocity is part of the explanation for terminal velocity, and you should be able to form equations (by setting equal to ) in order to calculate variables related to this.

Moments

Not only do you need to know how moments can be calculated (always remembering that it’s perpendicular distance, not just ‘distance, between the pivot and force), you should also be able to apply this to systems of levers, pulleys, or strings.

The key thing to bear in mind with these questions is that you can always break down complex systems into constituent parts. As long as the only forces ‘visible’ once the bits have been put back together are the external forces, you can create as many ‘internal’ forces (e.g. tension in ropes, or in linkages between train carts) as you need to do your calculations.

Logarithms and Exponentials

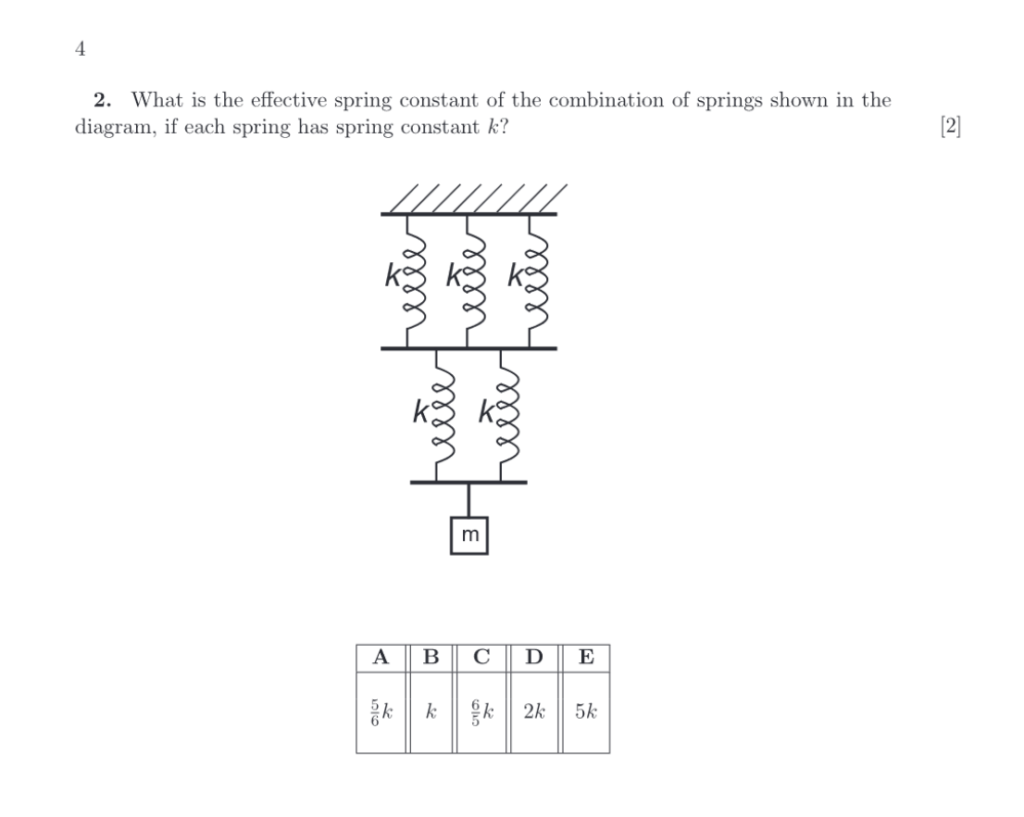
Springs

This, fortunately, is difficult for them to ask in an ‘interesting’ way – so it’s just a case of knowing and being able to apply:

Energy

Never forget your GCSE (or equivalent) topics!

Momentum

You must also be able to apply conservation of momentum, as well as conservation of energy. Impulse is very unlikely to arise, but if this was an area you struggled with at GCSE it’s worth making sure that just seeing the word doesn’t cause a panic!

Waves and Optics

This topic’s a bit more specific, but there’s still a lot of different things to revise:

Waves Basics

You must know the definitions (and units, if applicable), for all of these:

Longitudinal.
Transverse.
Amplitude.
Frequency.
Time Period.
Wavelength.
Speed of a wave (the wave front!).

Electromagnetic Spectrum

You should be aware of the nature and properties of electromagnetic waves in general, the really simple stuff like the fact they’re all transverse, and they all travel at the speed of light.

You should also be able to identify parts of the EM spectrum. Most students don’t have to learn the actual wavelengths of the EM spectrum for their A-levels, and so can put the spectrum in order, but couldn’t actually identify what kind of light might have a wavelength of 450nm, for example (it’d be visible!). For the PAT, make sure that you know the approximate bounds for the electromagnetic spectrum so that you can make ‘common sense’ estimates of what answer you’re expecting in the case of tricky questions, which helps you spot errors. Also, at interview this is one of those things they sometimes expect to be ‘common sense’ (we don’t understand how, either!).

Reflection

As well as the standard reflection equations (angle of incidence = angle of reflection), you should also be able to explain how total internal reflection works (which is actually based on refraction equations!).

Refraction

Learn and use Snell’s law, and make sure you remember that ‘n’ of air can be approximated as ‘1’, because n is the ratio between the speed of light in the material, and the speed of light in a vacuum. Make sure you can move from Snell’s law to the equation for total internal reflection. You should also be able to apply both of these to real-life applications such as prisms and optical fibres.

Standing Waves

Standing (or stationary) waves are one of the bits of physics which most students find to be incredibly tricky to imagine. Fortunately, you don’t need to know that much about them for the PAT! You should be able to explain how they form, and you should know how to relate the number of nodes to the wavelength and the length of the medium they’re forming in (or on). So for example, if I see the first harmonic of a wave on a string of length 1m, then the wavelength is 2m (because the first harmonic is one ‘loop’, or half the wavelength).

Electricity and Magnetism

These two subjects are very different, but still have a lot in common and a fair amount of crossover. That’s why we’ll be looking at them together:

Circut Basics

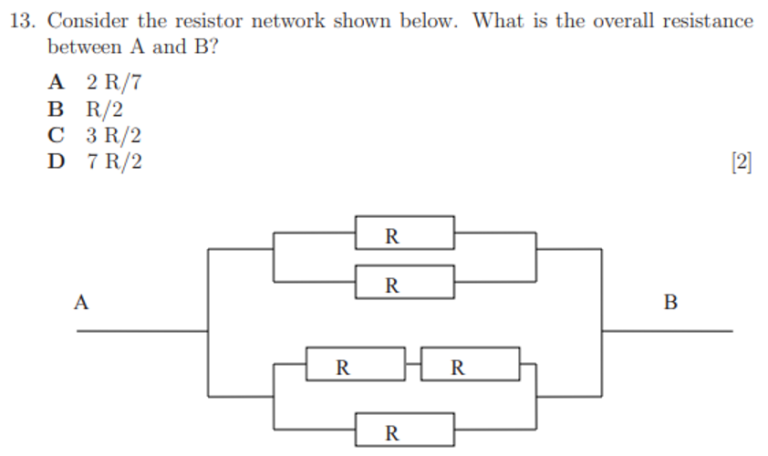
Common lower-mark questions will include finding equivalent resistance in parallel and series circuits, or calculating current or voltage with a need to find an equivalent resistance first. You should practice so that you’re able to do questions like this one from the 2009 paper as quickly as possible:

Make sure you can use all of the equations for current, voltage, power, resistance, and charge. It’s also important to be able to recognise all the common circuit symbols: batteries, resistors, lamps, diodes, capacitors, light dependent resistors, and thermistors.

If you haven’t been taught about capacitors and capacitance yet at school you should revise this before the PAT!
- Make sure to learn how you combine capacitors in series and parallel, which is the same as resistors just in reverse (you add them together when they’re in parallel, and do the weird reciprocal equation when they’re in series)

You should also make sure you remember how to add and divide voltages and currents in series and parallel sections of circuits, including understanding why you might set up a circuit in parallel (e.g. the lights in your house), rather than in series. If you’re not sure, think about what would happen if one of the bulbs broke and stopped letting current through.

Fields

You should know the equation for finding the force between two point charges, and the force on a point charge in a uniform electric field (is the one everyone forgets!).

You may see some questions (for example the last question on the 2013 paper) which also look at magnetic fields. According to the current version of the syllabus you do not need to know about magnetism, however if you have time it wouldn’t hurt to look ahead at this particular topic given how often it has come up in the past.

Photoelectric Effect

The PAT syllabus includes the ‘photoelectric effect’ as a topic you must know about – however the way it’s worded gives you a few hints at what sort of questions they might ask:

“photoelectrons are emitted if they are given sufficient energy to overcome the work function of the material, and how to find the energy of accelerated electron beams”

You’re actually quite unlikely to be asked anything about how the photoelectric effect supports the theory of wave-particle duality, because they’re concerned with much more practical things, like particle accelerators! The main equation you need here goes all the way back to your definition of voltage, and says that:

Energy = Charge x Potential Difference

Natural World

This is a subject that you won’t find in Physics-based admissions tests such as the NSAA and ENGAA, but it’s an equally important part of science that is necessary to be tested. Since it’s not as widely recognised, you may find it harder to find preparation material for it (which is something that PAT.Ninja provides plenty of!)

Atomic Structure

This is all stuff you’ve been doing for years now! Plus a bit of revision to make sure you can define ions, isotopes, and the three types of radiation.

Space

This is where the PAT goes back to primary school! You need to know the order, and names, of the planets. You also need to know what planets, moons, comets, and asteroids are (in very simple terms).

In general, this comes up in questions about eclipses, in which you’ll be given the diameter of the moon and sun, as well as the distance to one of them, and you’ll need to use ‘similar triangles’ (another GCSE topic) to be able to work out the missing dimension. This means you need to know that a solar eclipse is one where the moon gets in between the Earth and the Sun (so you can’t see the Sun), whereas a lunar eclipse is one where the Earth is directly between the Sun and the moon (so the moon is in shadow).

Satellites

Most of the stuff you need to know about satellites, is actually just circular motion but in a space-y context. Remember, that orbits can be circular or elliptical, but straight lines while in a radial gravitational fields wouldn’t work, unless the object was heading along a ‘radius’ (without some external force being applied to keep travelling in a straight line).

You should be familiar with the difference between a polar orbit (which is really low, and goes over the poles), and a geostationary orbit (which is quite high up, and over the equator). You also should be able to explain why you couldn’t make a geostationary orbit that was directly over Oxford, for example, using your knowledge of forces in circular motion.

As with PAT maths, let’s take a bit of time to try out some PAT Physics Practice Questions:

PAT Physics Practice Questions

PAT Physics Practice Question 1

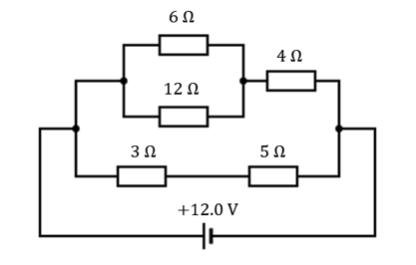
What is the overall resistance of the following circuit? [2]

A) 12Ω

B) 10Ω

C) 16Ω

D)8Ω

E)4Ω

The correct answer is E.

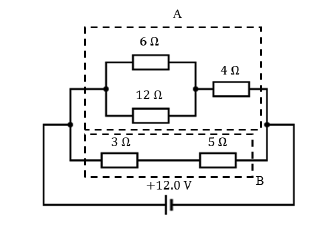
Break the resistors up into different blocks, as in the diagram below.

For block A:

R_A = 4 + ((6)(12))/(6 + 12) = 8Ω

For block B:

R_B = 3 + 5 = 8Ω

The overall resistance is therefore

R_Total = (R_AR_B)/(R_A+ R_B)

=((8)(8))/(8 + 8)

= 4Ω

PAT Physics Practice Question 2

Which of the following statements are correct regarding our solar system? [2]

1.The smallest planet is Mercury and the biggest planet is Jupiter.

2.Jupiter has more moons than Saturn.

3.Mercury is the only planet without moons.

4.As the mean distance from the Sun increases, the duration of the year on each planet increases.

5.As the mean distance from the Sun increases, the duration of the day on each planet increases.

A) 1 and 4

B) 1, 2 and 4

C) 1 and 2

D) 2 and 4

E) 1, 3 and 5

The correct answer is B.

Statement 1 is correct. Jupiter has 67 moons in total whereas Saturn has 62 hence statement 2 is correct. Venus also does not have any moons hence 3 is incorrect. Statement 4 is correct (Kepler’s Third Law). Statement 5 is not necessarily correct as duration of day depends on rate of rotation which has no correlation with distance to Sun.

PAT Physics Practice Question 3

(Please be aware that the PAT will no longer feature written questions of this style in 2024. Only Multiple-Choice Questions are included in the test)

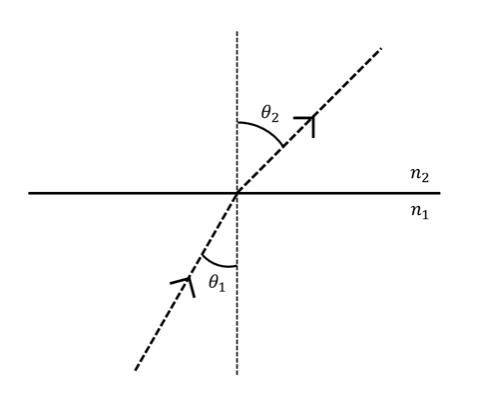
Sketch the path of light travelling from a medium of optical density n₁into a medium of optical density n₂, where n₁> n₂. Label the angle of incidence (θ₁) and the angle of refraction (θ₂). Using Snell’s law, derive the relationship between the critical angle (θ_c) and the angle of incidence. [7]

Carbon disulphide liquid is poured into a container made of crown glass . What is the critical angle for internal reflection of a ray in the liquid when it is incident on the liquid-to-glass surface? [3]

Answer:

Snell’s law:

n₁sinθ₁ = n₂sinθ₂

When the angle of incidence reaches a certain critical value, the refracted ray lies along the boundary and so the angle of refraction is 90°.

n₁sinθ₁ = n₂sinθ90

sinθ_c = n₂/n₁

When the light is incident on the liquid-glass surface, the critical angle is given by:

sinθ_c = n_glass/n_liquid

= 1.52/1.63

=0.93

θ_c ≈ 69°

PAT Physics Practice Question 4

(Please be aware that the PAT will no longer feature written questions of this style in 2024. Only Multiple-Choice Questions are included in the test)

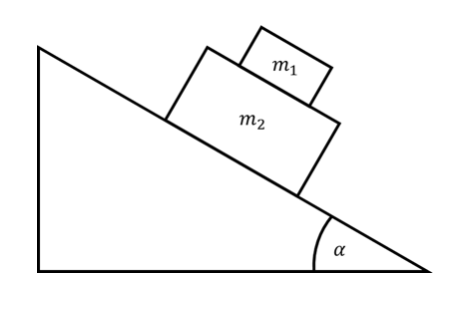
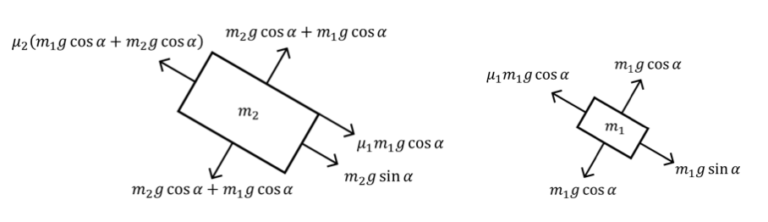
Consider the diagram below, where a mass m₁ rests on top of another mass m₂, which itself sits on plane inclined at an angle α. If the friction coefficient between m₁and m₂is μ₁ and the friction coefficient between m₂ and the inclined plane is μ₂ , determine:

a) the acceleration of m₂ ,

b) the acceleration of m₁with respect to the plane,

c) the acceleration of m₁with respect to m₂ . [10]

Consider the following free body diagrams of the masses m₁and m₂:

As shown, mass m₂experiences an extra force of m₁gcosα perpendicular to the slope due to the reaction force it exerts on m₁. It also experiences an extra force of μ₁m₁gcosα parallel to the slope due to the frictional force it exerts on m₁.

a) Resolve forces on m₂parallel to the slope and use Newton’s second law:

m₂a₂ = m₂gsinα + μ₁m₁gcosα – μ₂(m₁gcosα + m₂gcosα)

a₂ = g/m₂[m₂sinα + μ₁m₁cosα – μ₂(m₁+ m₂)cosα]

b) Resolve forces on m₁parallel to the slope and use Newton’s second law:

m₁a₁ = m₁gsinα – μ₁m₁gcosα

a₁ = g[sinα – μ₁cosα]

c) a′₁ = a₁ – a₂

=g[sinα – μ₁cosα] – (g/m₂)[m₂sinα + μ₁m₁cosα – μ₂(m₁+ m₂)cosα]

=g[sinα – μ₁cosα – sinα – (μ₁m₁/m₂)cosα(μ₂m₂/m₂)cosα + μ₂cosα

=gcosα [-μ₁– (μ₁m₁/m₂) + (μ₂m₂/m₂) + μ₂

=gcosα [-μ₁(1 + (m₁/m₂)) + μ₂(1 + (m₁/m₂)]

=gcosα(1 + (m₁/m₂))(μ₂– μ₁)

Final PAT Tips

We’ve focussed a lot on content knowledge here today, so let’s finish things up with some general PAT tips!

Within the PAT Syllabus, you’ll find this ominous sounding statement:

“Problems may be set which require problem solving based on information provided rather than knowledge about a topic”

What does this mean? This is essentially another way of say that the PAT has a heavy focus on application rather than base knowledge. Without practicing questions and past papers (and leaving time to review and learn from the questions you got wrong!) – the knowledge about a topic will only go so far.

Sometimes, you will be asked to learn a brand new way of working, and then to use that in the rest of the question. This isn’t a reason to panic, because they will always have given you the information you need!

It’s therefore a good idea to find a way of ‘actively reading’ the question, and making notes so that you don’t have to keep reading such large amounts of information over and over again. The key is to just take it a line, or even a word at a time, and don’t worry about figuring out ‘why’ something is if you don’t need to.

The PAT will sometimes ask things in a weird way which is not terribly familiar unless you’ve done lots of practice. That being said, it’s not supposed to be impossible. We’ll often see students who spend far too much time on questions because they’re worried about doing something which seems too ‘easy’. Don’t second-guess the examiners! Sometimes the 2 mark questions are just 2 mark questions, so you’ll need to learn how to prioritise.

Here are a few additinal tips to close things out:

Practice from any resources you can find, especially PAT past papers.
Using past papers from other Physics-based exams will also be helpful for refining your content knowledge and perfecting your multiple-choice skills.
There are a lot of equations you're going to need to memorise in order to get you through the exam, so put a heavy focus on these during revision.
Don't be afraid to leave questions for the end if you really can't answer it within 2 minutes or so.
If you still have questions to answer right before the end of the exam, be sure to leave some kind of answer, you won't lose any marks!

And there we have it, you’ve just made a great starting point for your PAT preparation. You now not only know what content knowledge you need to revise but also how the PAT functions and what you should expect on testing day.

Be sure to keep an eye for new PAT guides on Exams.Ninja, or jump straight into the worlds best PAT Preparation Platform to give yourself the best chance of success!

Oxford PAT Results 2024 – The Definitive Guide to your PAT Score

PAT Preparation: Your 6-Month PAT Preparation Timeline

PAT Calculus: Everything You Need to Know For The PAT

PAT Oxford: The Definitive PAT Starter Guide For 2024

Don’t start your preparation late, get ready for the PAT now!

With the PAT Preparation Platform, you’ll have everything you could need to achieve PAT success. You’ll get instant access to all of these amazing components:

Training Temple- Your revision plan will be sorted with over 100 expert tutorials to go through, along with plenty of exam tips.

Practice Dojo- With over 900 practice questions to take on, you’ll be able to practice all the way through to the exam date! Each question even comes with a fully explained solution to ensure you’ll get it right in future!

Exam Arena- Get access to 5 full PAT Past Papers, each with realistic exam conditions, full marking and worked solutions for every question!