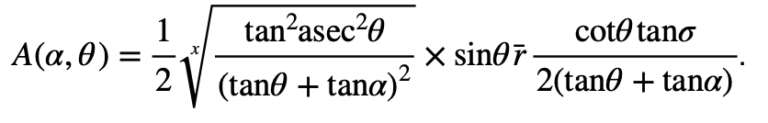YOUR ULTIMATE GUIDE
The Definitive Starter Guide To The MAT (2024)
Written by: Matt Amalfitano-Stroud
The MAT is an admissions assessment required for applicants who wish to study Maths or a related course at some universities. In this guide we’ll cover the essential test information, the different sections of the MAT and how to prepare for the test, along with some practice questions to get you started.
1/4
MAT BASICS: EVERYTHING YOU NEED TO KNOW
First, let’s cover the essential MAT information, including the different test sections, key dates, scoring, results and more. There’s a lot of information to process so we’ve broken down your most important MAT questions to help you understand everything. Let’s get started!


What is the MAT?
The Mathematics Admissions Test (MAT), is exactly what it sounds like – an admissions test for those applying to Mathematics related university courses. The MAT is used by a variety of universities in the UK and is taken at both Batchelor’s and Master’s levels in some cases.
It is produced and delivered for the University of Oxford in partnership with Pearson VUE using its dedicated testing system.
It’s a computer-based test made up of multiple-choice questions and two longer-written questions. It’s designed to be approachable by all students, including those without Further Mathematics A-Level or the equivalent.
What is the Structure of the MAT?
The MAT lasts 2 hours and 30 minutes. Its format is fairly unique compared to other admissions tests such as the TMUA. The paper contains 27 questions and two different question formats:
Questions 1 – 25 are multiple-choice questions, each featuring 5 answer options per problem.
Questions 26 and 27 are longer, written questions, each with multiple parts that are scored individually. These are based more on scenarios rather than basic problems, in which you will need to consider context and provide reasoning as well as solutions.
MAT Format Changes 2024
Pre-2024, the MAT featured a fairly different format in terms of its presentation and questions. In most previous years, the MAT was a paper-based test rather than computer-based (2023 saw an experimental hybrid format used).
The question structure was also vastly different as there were only 6 distinct questions, more of which were written questions. The basic format was as follows:
Question 1 was a multiple-choice question, with ten parts, each worth 4 marks.
Questions 2 – 6 were longer, written questions, each worth 15 marks. You would only attempt four of these depending on which degree you were applying for.
Why is the MAT Used?
The MAT is designed to test the depth of your understanding, and your ability to solve problems. Universities use it to differentiate between candidates who might look similar on paper otherwise – e.g. to decide between two applicants with similar A-Level predictions and GCSE grades. Universities can see your overall mark and how you did on the parts of each question. They use this to identify your strengths and weaknesses and how you think which helps them see if you would thrive in their courses.
The test requires you to think more deeply than your A-Level papers (or equivalent), and so at first, it will seem harder. But don’t worry, this is on purpose! Unlike A-Levels, it is very rare that people get full marks on the MAT, as they don’t want to set a paper that people will find easy – this won’t help them to differentiate between candidates.
Universities want to make you think so that they can see how you think.
Who Needs to Sit the MAT?
Since the MAT is a test of mathematics, it is commonly used to test applicants of relevant courses, including Mathematics, Computer Science, or any joint honours courses, such as Mathematics and Philosophy or Mathematics and Computer Science at an undergraduate level.
In the UK, there are three universities that use the MAT for their various mathematics degrees. Out of these three, the MAT is compulsory at one universities while the other two accept the results but do not require them for entry:
Bear in mind that your results will be automatically sent to Oxford if you are applying there. Your result will also be sent to Bath and Durham but they will not have access to them unless you grant permission.
Nottingham will not receive your results automatically, they will have their own systems in place to receive them but do not require you to send them if you do not wish for them to have access to them.
Which MAT Questions Should I Answer?
As mentioned, previous MAT papers featured some questions that were exclusively for applicants of certain courses.
However, with the new format, applicants will be required to complete all 27 questions in the test.
What are the Key Dates for the MAT?
Below are the important dates for the MAT this year, including registration deadlines and testing dates:
| Applicants Deadlines 2023 | |
|---|---|
| Registration Opens | 15th August 2025 |
| Registration Closes | 4th October 2025 |
| Submit Your UCAS Form (Oxford) | 15th October 2025 |
| MAT Testing Date | 22nd – 23rd October 2025 |
| MAT Results Released | November 2025 |
Where is the MAT Sat?
The MAT is sat within dedicated Pearson VUE testing centres. These are located all across the globe, including over 100 within the UK. You will need to select your test centre during the booking process for your test.
If you have a disability or special requirement and are normally entitled to support for exams, let your centre know when you register as there will be access arrangements available for you.
How Much Does the MAT Cost to Sit?
Nothing. There’s no entry fee to sit the MAT.
How Hard is the MAT?
The MAT is designed to test you by applying the concepts you’re familiar with from A-Levels but in unusual ways. You are expected to think more deeply than your A-Level (or equivalent) papers, and so initially the MAT is likely to seem harder. Also, you may find the MAT harder if you are a less creatively inclined mathematician, but with the right preparation you won’t need to worry!
Can you Resit the MAT?
If you aren’t happy with your MAT score, unfortunately, you are not able to resit later in the year, as the test is run only once a year. If you decide to reapply to these universities next year, you will have to sit the MAT again just as you do this year.
How is the MAT Scored?
For 2024, the MAT will be scored based on raw marks, with a total of 100 marks available in the paper. Due to the increase in multiple-choice questions, the full selection of 25 questions are now worth 75 marks in total.
Based on practice MAT test provided by Oxford, these marks are split up as follows:
- Questions 1 – 10: 2 Marks each
- Questions 11 – 20: 3 Marks Each
- Questions 21 -25: 4 Marks Each
Questions 26 and 27, the two multi-part questions, are each worth 15 points. Based on the practice test, we can see that each part is worth 2 – 6 marks based on its complexity.
There are no score conversions and your results will be reported either as a score out of 100 or as a percentage.
How do you get your MAT results?
Oxford Applicants are automatically sent an email with their results in January. You do not automatically receive a result for the MAT. If you want to find out how you have done you should email the university’s maths department with your name, UCAS ID, and MAT registration number and request feedback. They will not be able to give you any feedback until the admissions cycle is over, so you should email after March 31 next year.
Discover more about MAT scoring in our MAT Scoring and Results Guide.
It’s never too early to begin your MAT preparation, so start your journey today with MAT.Ninja!
With the MAT.Ninja Preparation Platform, you can access 100’s of realistic practice questions and every MAT past paper for free! Sign up today to begin your MAT prep.
2/4
MAT SYLLABUS: WHAT DO YOU NEED TO REVISE?
The MAT is designed to be accessible to any Maths student at the start of their second year of A-Levels or equivalent. All you need is knowledge from the first year of A-Level Maths, and a couple of topics from the beginning of the second year, so let’s run down everything that may be covered in your MAT paper.



The MAT syllabus covers the following ten areas, so it’s a good idea to make sure you are familiar with them early on in your preparation:
- The quadratic formula
- Completing the square
- Discriminant
- Factorisation
- The Factor Theorem
- Simple simultaneous equations in one or two variables
- Solution of simple inequalities
- Binomial Theorem with positive whole exponent
- Combinations and binomial probabilities
- Derivative of xa, including for fractional exponents
- Derivative of ekx
- Derivative of a sum of functions
- Tangents and normals to graphs
- Turning points
- Second order derivatives
- Maxima and minima
- Increasing and decreasing functions
- Differentiation from first principles
- Indefinite integration as the reverse of differentiation
- Definite integrals and the signed areas they represent
- Integration of xa (where a ≠ -1) and sums of these
- The graphs of quadratics and cubics
- Graphs of sin x, cos x, tan x, √x, ax, logax
- Solving equations and inequalities with graphs
- Laws of logarithms and exponentials
- Solution of the equation ax = b
The relations between the following graphs:
- y = f (ax)
- y = af (x)
- y = f (x – a)
- y = f (x) + a
- y = f (x)
- Co-ordinate geometry and vectors in the plane
- The equations of straight lines and circles
- Basic properties of circles
- Lengths of arcs of circles
Solution of simple trigonometric equations. The identities:
- tan x = sin x / cos x
- sin2 x + cos2 x = 1
- sin (90° – x) = cos x
Periodicity of sine, cosine and tangent. Sine and cosine rules for triangles.
- Sequences defined iteratively and by formulae
- Arithmetic and geometric progressions
- Their sums
- Convergence condition for infinite geometric progressions
Exams.Ninja Tip
The MAT syllabus was changed in 2018, adding and adjusting required knowledge throughout most subjects. Some of these changes were minor, but it is still important to make sure you are reading the 2018 version of the MAT syllabus when beginning your preparation.
This will also affect your use of past papers. When using past papers, be aware that the papers dated 2017 or earlier will be following the old syllabus and thus may have questions which are no longer relevant in the MAT. It is still worth taking on these papers though as they provide tonnes of practice questions from the official source.
You can download the official MAT syllabus document here.
Sequences and series are the only topics which you may not come across until the second year of A-Level Maths. Ask your teacher if you can cover these before October half-term, or if you can borrow a textbook to teach yourself these bits.
You won’t get a formula booklet or be allowed your own when you take the MAT so you should make sure you have all the formulae and identities here memorised for when you sit it.
3/4
MAT REVISION TIPS
Once you are comfortable with the material on the syllabus, it’s time to get your practice and preparation started! The tips will help you make the most of your time before the test, so let’s do this.
1. Create a Plan
Before you think about jumping into past papers and practice questions, you should first think about how you’re actually going to approach this. In other words, you’re going to need to make a plan.
We wouldn’t recommend leaving any less than four weeks to prepare for a typical admissions test, but mathematics can generally be more difficult to get so we would suggest six weeks as a minimum. We’ve even outlined how you can structure your preparation over six months!
The essential three elements to include in this plan are revision, practice questions and mock exams. Start off by using your notes and resources to gain a better understanding of the theory behind the maths. Then take some time to get to know the question structure and techniques with some practice questions (preferably with worked solutions). Lastly, as you get closer to the test date, begin to sit more and more past papers in realistic exam conditions to ensure you get to grips with your exam technique.
Exams.Ninja’s MAT Preparation Platform contains everything you need to work through your preparation, so be sure. to create an account today to try it for free!
2. Pay Attention in Class
As we’ve already said, all of the required knowledge for the MAT will be covered in your first and early second years of A- Levels (or equivalent). Your class is where your MAT preparation actually starts, so be sure to make the most of the learning time you have.
Be sure to make detailed notes that you can refer to later, this will be a lifesaver when you’re in the early stages of practice questions for the test. Some teachers may also provide their own teaching resources for you to take home, such as worksheets and presentations. Anything you can get may come in handy when you’re fully stuck into your MAT prep, so gather your resources early and keep them organised.
Lastly, if you’re not getting something in class, don’t be afraid to seek extra help from your teacher, even if it’s after class. It’s vital that you understand as much as possible from the syllabus, so it would be a waste to not take the chance to learn more from an expert.
3. Practice Questions are Key
Mathematics is a pretty practical subject in reality. There isn’t a lot of factual information to memorise other than rules and formulas. These are incredibly important to remember, but we feel that the best way to cement them into your brain is with practice questions.
It’s common knowledge that in many cases, the best way to learn is by doing, and implementing your maths knowledge into practice questions is very easy and effective to do. We wouldn’t suggest you take all your questions from past papers, as you’ll need those for mock exams (although there 18 to currently pick from). Instead, look into using an MAT question bank – the best ones should have 100s of unique questions to answer.
Alongside the number of questions, you should also seek out worked solutions to go with them. You’re not going to get every question right when you’re starting out, or even when you’re sitting the final exam! Therefore, worked solutions will allow you to see where you went wrong and understand what the correct solution is in a clear manner. You can see how good worked solutions should look down below.
4. Test Your Skills Regularly
Sitting mock papers shouldn’t just be saved for the last few days of your preparation, you should be taking them on regularly. With papers available for free dating as far back as 2007, you aren’t likely to run out if you use them sensibly! (Remember that pre-2018 papers are based on a slightly different syllabus).
We would actually say that looking at a mock paper should be one of the first things you do in your preparation plan. At this stage, you shouldn’t be too concerned about completing it within the 150-minute time limit or getting a good score. Instead, just use the time to get an understanding of the exam format and the types of questions that will be asked of you.
As you move forward in your prep, you can gradually become more and more strict with yourself until you’re sitting papers in exam conditions and achieving scores that would get you an offer!
As well as learning from the papers, it’s also important to make sure you’re monitoring your progress. Mark your papers thoroughly and pay attention to the types of questions you’re getting right and wrong as this will help you influence your revision to strengthen your weaknesses.
Exams.Ninja Tip
It doesn’t matter too much what order you take the past papers in, but we would suggest saving the most recent past paper for the last days before your test date. This paper will be the most similar to the one you will be sitting as it was developed most recently. Of course, this may be untrue if any syllabus or format changes have been made on the year you take the test.
Exams.Ninja presents the ultimate platform for your MAT preparation!
With over 90 in-depth tutorials, more than 700 fully explained questions and 15+ full MAT past papers, MAT.Ninja gives you everything you need to pass the MAT with confidence!
Try it for free today to see how you can boost your MAT score.
4/4
MAT PRACTICE QUESTIONS
With all the basics of the MAT now out of the way, the final thing to do here is to check out some questions. This collection of practice questions will provide you with a good entry point to your MAT preparation.
MAT Question 1 Example 1
The equation
4x – 1 – 2 x + 1 = k
where k is a real number, obtains its minimum value when
A) x = 0
B) x = 1
C) x = 2
D) x = -1
E) x = -∞
The correct answer is C.
4x – 1 – 2 x + 1 = k = (22x/4) – 2(2x) = k
Let 2x = y, then y²/4 – 2y = k.
We want to find the minimum of y² – 8y = 4k, so we can initiate and set to zero to see that y = 4 is a stationary point. You can take the second derivative to verify that it is a minimum (as 2 > 0). So we must have 2x = 4 ⇒ x = 2. Alternatively, you can check each option quickly to see this must be the case.
MAT Question 1 Example 2
Let n be an integer and define the functions f(x) and g(x) by
f(x) = x²
g(x) = (x + 4)n – (x + 1)n(x+1)n²
Then x² + 3 is a factor of g(f(x)) for
A) Even n
B) n = 0 only
C) Odd n
D) n = 0
E) n = -1 only
The correct answer is D.
We know that (x³ + 3) is a factor of g(f(x)) which implies that x + 3 is a factor of g(x). So in particular, we have that g(-3) = 0 ⇒ (-1)n – (-2)n (-2)n = 0.
We see general even and odd values of n do not work. Plugging in values for n = 0, -1, we see that both are valid solutions.
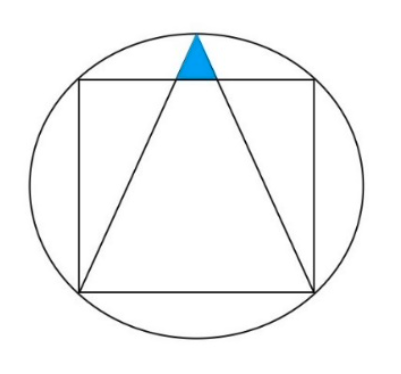
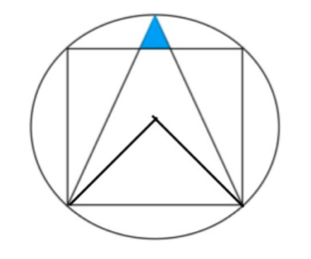
MAT Question 1 Example 3
A square is inscribed in a circle of radius √2. An isosceles triangle is inscribed in the square. What is the area of the shaded region?
A) 5√2 – 7
B) 1/3
C) 4√2
D) 1/10
E) √2 – 1
The correct answer is A.
By Pythagoras on the bold right angle triangle, the side length of the square is 2. The height of the shaded triangle is therefore √2 – 1, and the height of the large triangle is 1 + √2.
Considering their respective angles, note that the small and large triangles are similar with a scale factor of (√2 – 1)/(√2 + 1). Half the base of the small triangle is therefore equal to (√2 – 1)/(√2 + 1) so the small triangle has area (√2 – 1) * (√2 – 1)/(√2 + 1).
MAT Question 1 Example 4
To be awarded a £100n prize, students must score at least 50% on n different exams, where n is a positive integer. Suppose that 6 students are taking these exams, and for every exam, every result is equally likely. Furthermore, individual exam results are independent. What is the probability that 2 of these 6 students received a £100n prize?
A) 2-2n
B) (15(2n – 1)4) / 26n
C) (2n – 1)4 / 22n
D) ((2n – 1)²) / 22n
E) (6(2n – 1)4) / 26n
The correct answer is B.
For these 6 students, the probability of the award is p = 1/2n.
Each student can either get the award with probability p or not get the award with probability 1 – p, independent of all the other student’s performances. This is a binomial probability and so the answer is
6C2 x (1/2n)² x (1 – 1/2n)4 = 15 x ((2n – 1)4) / 26n
MAT Question 2 Example
A function f(x) is called ‘even’ if f(x) = f(-x) for all x and it is called ‘odd’ if f(-x) = –f(x) for all x.
(i) Show that f(x) = x² is an even function and g(x) = x³ is an odd function.
(ii) Must a polynomial be either an odd or even function? Explain your answer.
(iii) What is the only function that is both odd and even? Show that this is the only such function.
Suppose that f(x) is an even function and g(x) is an odd function.
(iv) Show that fg, gf and f² are all even functions.
Now let h(x) be some function. Define
f(x) = (h(x) + h(-x))/2 g(x) = (h(x) + h(-x))/2
(v) Hence show that any function can be written as the sum of an odd and an even function.
(vi) Show that every function can be written as a unique sum of an even and odd function.
(i) [2 Marks] f(-x) = (-x)² = x² = f(x) and f(-x) = (-x)³ = –x³ = – 9(x).
(ii) [2 Marks] No. A correct counterexample is, for example, f(x) = 1 + x with f(-x) = 1 – x which is neither equal to f(x) nor –f(x) for all x.
(iii) [2 Marks] If f is both even and odd, then for all x, f(-x) = f(x) and –f(-x) = f(x). Adding these together gives f(x) = 0 for all x. Thus the only such function is the function that is zero everywhere.
(iv) [3 Marks] g(-x) = f(g(-x))(-g(x)) = f(9(x)) = fg(x) for all x.
gf(-x) = g(f(-x)) = g(f(x)) = gf(x) for all x.
f²(-x) – f(f(-x)) = f(f(x)) = f²(x) for all x.
(v) [3 Marks] f(x) + g(x) = (h(-x) + h(x)) / 2 = –g(x) so g is odd. Given any function h we can always construct this f and g. Therefore every function can be written as the sum of an odd function and an even function.
(vi) [3 Marks] Assume that h can be written in two ways, as the sum of an even and odd function i.e. h(x) = f1(x) + g1(x) = f2(x) + g2(x) where fi(x) are even functions and gi are odd functions. This means that f1(x) – f2(x) = g2(x) – g1(x). Note that the left side of the equation is an even function, and the right side is an odd function. So these must be equal to 0, from part (iii). This implies that f1 = f2 = f and g1 = g2 = g. So h(x) = f(x) + g(x) is the unique decomposition in this way.
MAT Question 4 Example
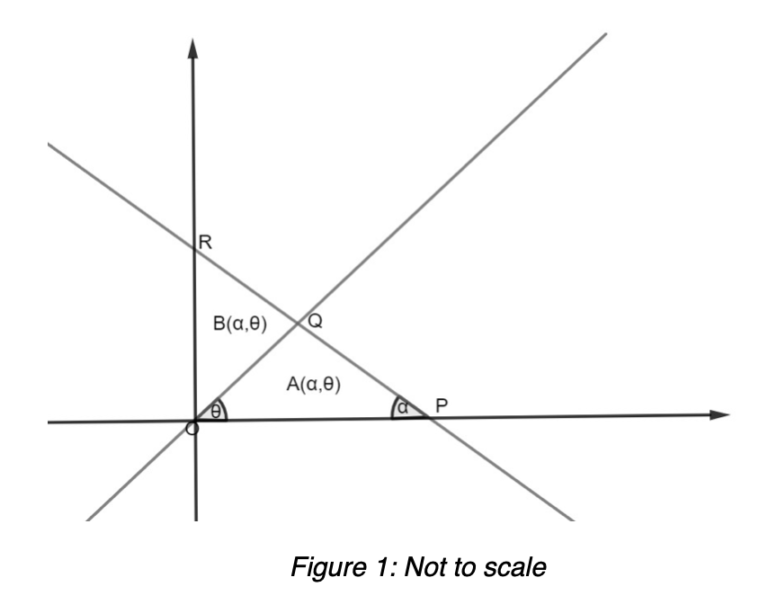
The diagram shows two lines in the plane, intersecting at a point Q. The line joining O and Q creates an angle θ with the x axis, while the line joining P, Q and R creates an angle α with the x axis, as shown in the diagram. Point P is located at (1,0).
(i) Find, in terms of α, the equation of the line joining points P, Q and R.
(ii) Find, in terms of θ, the equation of the line joining O and R. Hence write, in terms of α and θ, the coordinates of point Q.
Triangle OPQ has area A(α, θ) and triangle OQR has area B(α, θ).
(iii) Give an example of an α and θ such that A(α, θ) = B(α, θ). In addition, show that when A(α, θ) = B(α, θ), A(α, θ) is independent of θ.
(iv) Find an expression for A(α, θ) in terms of α and θ.
(v) Now let α = π/4. Find the value of tan(θ) such that A(π/4, θ) = 1/2 B(π/4, θ).
(i) [2 Marks] Using trigonometric relations on triangle POR, we can see that R is located at (0, tan α). The gradient of the line is –tan α/1 – tan α. The equation of the line is y – 0 = – tan α(x -1) which simplifies to y = – tan α(x -1).
(ii) [3 Marks] We know that the gradient of this line will be tan θ. Since the line goes through the origin, the equation of the line is y = xtanθ.
To find the coordinates of Q, we calculate the point of intersection between the two lines. xtanθ = -xtanθ(x – 1) and solving for x gives x = tanα / (tanθ + tanα). The y coordinates is y = tanθtanα / (tanθ + tanα).
(iii) [3 Marks] The simplest example of when A(α, θ) = B(α, θ) = B is when triangle POQ is isosceles and the line OR bisects PQ. This occurs when α = π/4 and θ = π/4.
The area of triangle POQ can be calculated using A = 1/2 bh where b is the base and h the height of the triangle. In this case b = 1 and h = tanα so A(POQ) = 1/2 tanα. We want A(α, θ) to be equal to exactly half this area, so A(α, θ) – 1/4 tanα which is independent of θ.
(iv) [4 Marks] We first calculate the length OQ Pythagoras.
|OQ|² = ((tanθtanα / (tanθ + tanα))² + (tanα / (tanθ + tanα))² = (tan²α(1 + tan²θ) / (tanθ + tanα)² = (tan²αsec²θ) / (tanθ + tanα)².
Then we can determine the area of the triangle using A = 1/2absinC. In this case…
(v) [3 Marks] When α = π/4, A(π/4, θ). The area of triangle POR is 1/2 when α = π/4. For A(π/4, θ) = 1/2B(π/4,θ), we want A(π/4, θ) = 1/6. Then we must have 1/6 = 1/ (2tanθ(1 + tanθ). This simplifies to the quadratic tan²θ + tanθ – 3 = 0 and solving for tanθ gives tanθ= (-1 ± √1-4(-3)) / 2 = (-1 ± √13) / 2. For 0 < θ < π/2, we must have tanθ = (-1 + √73) / 2.
MAT Question 6 Example
Some people are dealt cards which tell them exactly how to act. They say either: “You must always tell the truth” or “You must lie exactly once”. Each person can see everyone else’s cards.
(i) Suppose that there are two people and one of each type of card. First, person A says: “person B has the liar card”. And person B says: “person A has the liar card”. Then, A says: “Today is Monday”, and B says: “I have the truth card”. Who has the liar card?
For the rest of the question assume that there are more than one of each card (so A and B can have the same type of card).
(ii) Does the above conversation contain enough information to know which cards A and B have? Explain your answer and give any conclusions that can be made.
(iii) Suppose a new person C says first: “B has a liar card” and then “I have a truth card”. Does this change the conclusions you can make?
(iv) A new person D enters the room. And players A-D are re-dealt cards.
Person A says: “I have a truth card” and “It is sunny”.
Person B says “It is after 2 pm” and “Exactly one of us has a truth card”. Person C says “It is not sunny” and “Person A has a truth card”.
Person D says “5 is less than 3” and “It is before 2 pm”.
Who has the truth card?
(i) [2 Marks] First let us condition on the card that A receives. Let’s assume it is the truth card. This implies that B has the liar card and it is a Monday. But this means that both of person B’s statements are lies, which is a contradiction – as they can only tell exactly one lie. So, A must have the liar card.
(ii) [5 Marks] Exactly the same line of reasoning holds and shows that A must have the liar card. If person B has a truth card then all of B’s statements are true and, provided it isn’t Monday, exactly one of A’s statements is a lie – so this situation is consistent. If person B has a liar card then B’s second statement is a lie, so B’s first statement is true which gives, as desired, that A has a liar card. Person A is then telling exactly one lie, as desired, provided it isn’t Monday. Therefore, B can have either card.
(iii) [3 Marks] If C has a truth card then B must have a liar card. If C has a liar card then C’s second statement is the lie so “B has a liar card” is true. Therefore, B has a liar card.
(iv) [5 Marks] D’s first statement is an obvious lie so D has a liar card and it is before 2pm. This makes B a liar, so it is true that exactly one person has a truth card. Suppose that C has a truth card. Then A has a truth card. This contradicts B’s true statement, so C has a liar card. Thus, by elimination, A must have the only truth card.
If you’re looking for even more MAT practice questions, you can more for free when you create a free account with MAT.Ninja!
That covers just about everything you need to know for the basics of the MAT! Of course, there is much more to learn in regard to the syllabus and questions, so be sure to gather resources that you feel will help you develop your skills and understanding.
Combine all your MAT preparation in one comprehensive package with Exams.Ninja.
Exams.Ninja’s MAT Preparation Platform will help you optimise your revision in an easy and enjoyable way. With the MAT.Ninja, you’ll get access to:
Training Temple – 99 expert tutorials covering the full syllabus of the MAT, designed to leave you as an MAT expert.
Practice Dojo – over 700 practice questions, each one matching the difficulty of the actual MAT and each with a fully worked solution to help you understand the maths.
Exam Arena – Attempt every MAT past paper in a realistic exam simulator that tracks your results and provides worked solutions for every question.
You can try the platform for free by signing up today!