ENGAA GUIDE

 

ENGAA Section 1B: Your Guide to Advanced Mathematics and Physics

Written by: Matt Amalfitano-Stroud

Please be aware that, as of 2024, the Engineering Admissions Assessment (ENGAA) is no longer being used by the University of Cambridge. Cambridge applicants for Natural Sciences, Engineering, Veterinary Medicine and Chemical Engineering & Biotechnology will be required to sit the Engineering and Science Admissions Test (ESAT). 

The ENGAA is a massive part of your Cambridge Engineering application, so you need to make sure you’re confident when you enter that examination. It’s split into two sections, Sections 1 & 2, and Section 1 is split further into Sections 1A and 1B. Section 1B is all about advanced mathematics and physics, so let’s take a look at what you need to know and how you can optimise your revision! 

Exams Ninja Question Mark Icon
1/5
Exams Ninja Paper 1B Icon
2/5
Exams Ninja ENGAA Knowledge Icon
3/5
Exams Ninja Preparation Pencils Icon
4/5
REVISION AND EXAM TIPS
Exams Ninja Multiple-Choice Questions Icon
5/5
PRACTICE QUESTIONS

1/5

BASICS OF THE ENGAA

First things first, let’s go over the key information you need to know about the ENGAA.

Exams.ninja over questions

What is the ENGAA? 

The Engineering Admissions Assessment (ENGAA) is extremely self-explanatory. You’ll be taking this assessment during your application for Engineering and Chemical Engineering at the University of Cambridge. The ENGAA is a pre-interview assessment and in 2023, it will be sat on October 18th, a few weeks earlier than previous years. Thankfully, there is no fee required for taking the ENGAA.

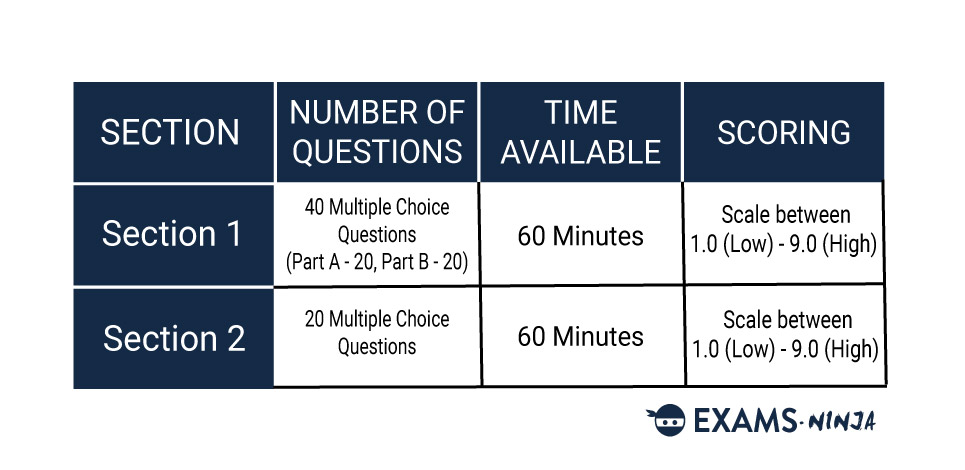
The ENGAA is split into 2 main sections, Section 1 and Section 2. Section 1 is split into two more parts, Section 1A and Section 1B. Throughout Section 1, you’ll be answering a total of 40 questions based on mathematics and physics (20 for each sub-section). 

Section 1A covers your core topics in maths and physics and is typically stuff that you should know from GCSE and early A-Levels.

Section 1B takes things further by looking at Advanced Mathematics and Physics. These 20 questions will be a lot tougher and will require more in-depth knowledge of maths and physics, although it will still be covering topics that you should be familiar with. This section doesn’t focus so much on testing completely different skills than Section 1A, but rather expands on what has already been covered.  

Section 2 doubles down on Advanced Physics, with 20 more multiple-choice questions to complete in 60 minutes. These questions will be tough, so make sure you’re prepared for them! If you’re not sure where to start, we would recommend our ENGAA Section 2 Guide!

Here’s a quick summary of the test format: 

ENGAA Test Format

ENGAA Format Table

How is the ENGAA Scored? 

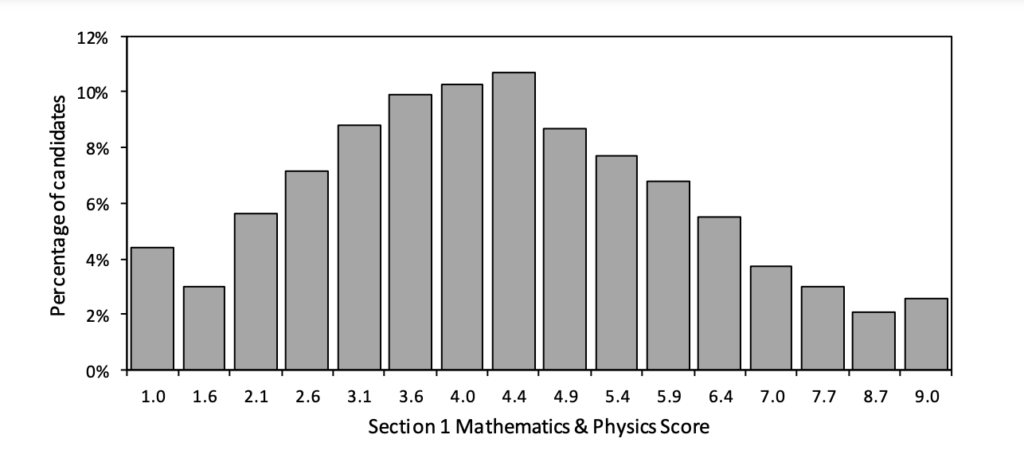
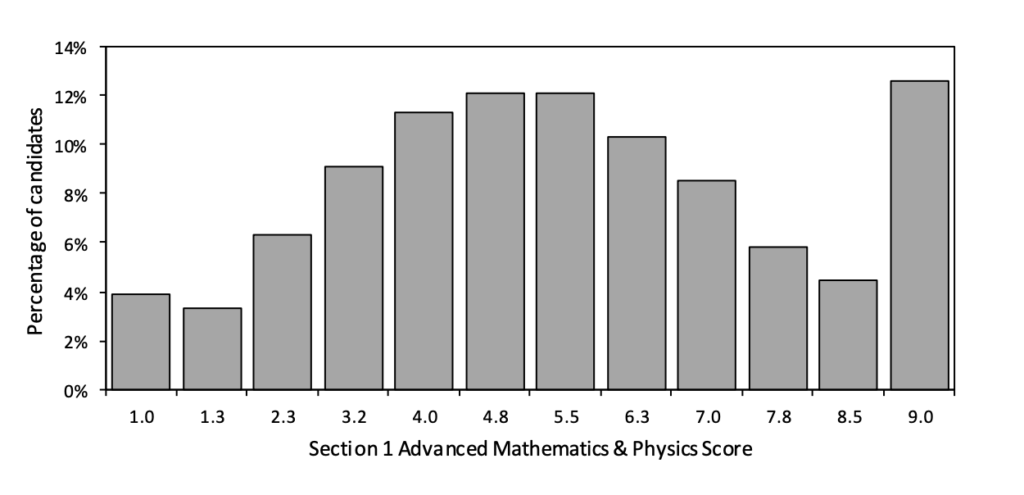
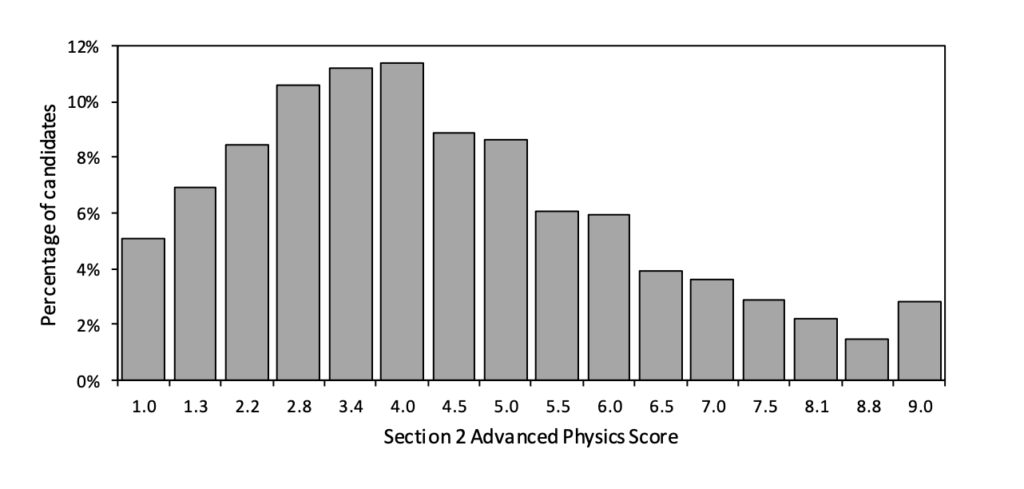
The scoring system in the ENGAA is pretty simple. Each section (including each part of Section 1) is scored on a scale between 1.0 (low) and 9.0 (high) which is converted from your raw marks based on your correct answers. Here are the Score Distributions for the ENGAA in the 2021 admissions cycle.

ENGAA Section 1A Score Distribution (2021)

ENGAA Section 1A Results Distribution 2021

ENGAA Section 1B Score Distribution (2021)

ENGAA Section 1B Results Distribution 2021

ENGAA Section 2 Score Distribution (2021)

ENGAA Section 2 Results Distribution 2021

You can see from these charts that the average scores didn’t change too much throughout each section, with the exception of Section 1B which had an abnormal amount of applicants score a 9.0 (perhaps they used our ENGAA Preparation Platform!). In fact, every section of the exam saw a small spike of students scoring full marks, so it’s possible to ace the paper if you put the work in beforehand!

There’s a pretty clear trend in each Section that will show you the kind of score you should be aiming to reach for a successful application. Generally, you’ll be wanting to score higher than the most common scores, so aiming for at least a 4.5 will increase your chances of getting an offer. 

There’s a lot more to learn about the ENGAA, so check out our Definitive ENGAA Guide.

Advance your skills in maths and physics in time for the ENGAA!

 
 
 
 

The ENGAA Preparation Programme features tons of resources all available instantly! With over 100+ tutorials and 900+ practice questions, your revision will be taken to the next level! Best of all, you can try it for free now!

 
 
 
 
 
 
 
 
 
 
TRY NOW FOR FREE

2/5

WHAT TO EXPECT FROM THE ENGAA SECTION 1B

The ENGAA isn’t the most complex exam in the world, at least not in terms of its format and layout. Still, it’s sensible to be familiar with how the assessment looks and works, so let’s check it out!

Exams Ninja Paper 1B Icon

The ENGAA isn’t anything mind-blowing when it comes to how it’s presented, but that just means it’s nice and simple, allowing you to focus on answering the questions.

Sections 1A and 1B are laid out pretty much identically, barring the content within the questions. Each sub-section, referred to as “Part A” and “Part B” in the paper, is labelled and separated from each other, so if you’re unsure which part you’re currently on, just look for the title page. Keep in mind that the ENGAA is split between two papers, so Section 2 won’t be on the paper that you’re initially given. 

Exams.Ninja Tip 

The questions in Section 1 are numbered from 1 – 40, meaning there is no split in numbering between Part A and Part B. Therefore, another way of checking which part you’re on is checking the question number, if you’re on question 21 or above, you’re in Part B!  

 
 
 
 
 
 
 
 

Each page will contain one or two questions depending on their length and amount of answer options. Speaking of which, each question will have a maximum of eight answers to choose from, all of which are labelled from A – H. 

Here’s what a typical page will look like in the ENGAA: 

ENGAA Section 1B Example Page

ENGAA Section 1B Example Page

The amount of free space you get will depend on the size of the question, but you’ll need to make sure you make the most of what is given, as you will not be allowed additional paper for working out. Your answer sheet, which is separate from the questions, will be reserved for final answers only, no rough work is permitted on it. 

3/5

ESSENTIAL INFORMATION FOR ENGAA SECTION 1B

There’s a lot to revise when it comes to the ENGAA, especially for the advanced questions. This is a rundown of the essential bits to revise before you take the exam. 

Exams Ninja ENGAA Knowledge Icon

First of all, let’s take a look at the official specification for the ENGAA. The specification provides an outline for all the knowledge applicants are expected to have when taking the assessment. We’ve already looked at the specification for the basic mathematics and physics needed for Section 1A in our ENGAA Section 1A Guide, so let’s jump straight into Advanced Mathematics!

Algebra and Functions

Algebra is used in all sorts of mathematics, so this is one that you really need to understand. Some of the things you’ll be expected to know are:

  • The laws of indices for all rational exponents.
  • Using and manipulating surds, including the simplification of expressions contains surds.
  • Quadratic functions, including their graphs.
  • The algebraic manipulation of polynomials.
  • Solving linear and quadratic inequalities.
  • The properties of common functions, such as “f(x) = |x|” and “fx = √x”.

Try out our Practice Questions relating to this topic here! 

Sequence and Series

Sequence and series are all about recognising, identifying and progressing numerical patterns, so you should hopefully be able to recognise a question about it when you’re sitting the ENGAA! Some of the areas covered in the exam include:

  • Arithmetic series.
  • Finite geometric series and convergent geometric series.
  • Binomial expansion of (1 + x)n.
  • The notions of n! and (n r).

Two-Dimensional Coordinate Geometry

Geometry is the mathematics of shapes, so you’ll need to perfect your skills with graphs, angles and converting equations. You’ll need to brush up on the following:

  • Straight-line equations, including “y - y1 = m(x - x1)” and “ax + by + c = 0”.
  • The coordinate geometry of a circle, with the equations “(x - a)2 + (y - b)2 = r2" and x2 + y2 cx + dy + e = 0".
  • The use of various circle properties (e.g. angles in the same segment are equal & the angle of a semicircle is a right angle).

Try out our Practice Questions relating to this topic here! 

Trigonometry

The triangular offshoot of geometry, there are plenty of unique rules at play that you’ll need to revise, including:

  • Sine, cosine and tangent values, functions and rules.
  • The area of a triangle in the form of "1/2absinC".
  • Radian measure.
  • Solving simple trigonometric equations.

Exponentials and Logarithms

Exponents and their inverse, logarithms, will be covered in the ENGAA, so you’ll want to revise the following:

  • y = ax and its graph.
  • The laws of logarithms, including “ab = c <=> b = loga c” and “log a x + logay = loga (xy)”.
  • Solving equations in the form of "ax = b”.

Try out our Practice Questions relating to this topic here! 

Differentiation

The ENGAA will require you to find derivatives and answer questions based on them, so you’ll need to revise the following: 

  • The derivative of f(x).
  • Differentiation of xn for the rational n.
  • Second-order derivatives.
  • The application of differentiation relating to gradients, tangents, normals, stationary points and increasing/decreasing functions.

Integration

Integration is very interlinked with geometry, so you’ll need to make sure you have the following knowledge prepared for the exam: 

  • Definite integration in relation to the axis between a curve and an axis.
  • Definite and indefinite integrals within xn.
  • The Fundamental Theorem of Calculus.
  • Combination of integrals.
  • Solving differential equations in the form of “dy/dx = f(x)”.

Graphs of Functions

Graphic interpretations of functions are extremely handy in mathematics, but learning to use and create them is pretty difficult. You’ll want to revise your knowledge on the following:

  • Recognising and sketching graphs of common functions (specifically those that have featured within the ENGAA specification).
  • The effects of simple transformations on graphs of “y = f(x)”.
  • Altering values of m and c.
  • Altering values of a, b and c in “y = (x + b)2 + c.”
  • Using differentiation to determine graph shapes of a given function.
  • Solving equations using geometric interpretation.

Try out our Practice Questions relating to this topic here! 

That’s a lot of maths to remember! However, that’s only half of it, as we’ve now got Advanced Physics to go through. Let’s take a look!

Forces and Equilibrium

These are the basis of all physics and super important to revise! Topics to look at include: 

  • The nature of scalars.
  • The nature, components and resultants of vectors, including coplanar vectors.
  • Moments, including those defined as force x perpendicular distance from the point to the line of action of the force.
  • Normal and frictional components of contact forces.
  • The terms “smooth” and “rough” in the context of physics.
  • The concept of “centre of gravity”.
  • Solving problems that involve the equilibrium of rigid bodies under coplanar forces.

Try out our Practice Questions relating to this topic here! 

Kinematics

This one is a classical branch of mechanics involving the calculation of possible motion without regard to related forces. It goes hand-in-hand with mathematics, so there are a lot of techniques and equations you’re going to need to remember, including:

  • The equation “power = force x velocity”.
  • The equations of motion; “v = u + at”, “s = ut + (1/2)at2”, “s = (u + v)t/2” and “v2 = u2 + 2as”.
  • The use of graphical methods involving acceleration, displacement, distance, speed, time and velocity.
  • The use of graphical representations of one-dimensional motion.

Newton’s Laws

Newton’s laws of motion are 3 essential rules that will apply to any kind of mechanical science that you use. They are as follows:

  1. An object will not change motion unless a force acts on it.
  2. The force of an object is equal to its mass multiplied by its acceleration.
  3. When two objects interact, they apply forces to each other in opposite directions and of equal magnitude. 

You’re going to need to be able to use these rules in a variety of ways, including:

  • Application to linear motion of point masses moving under the action of forces.
  • Solving problems that involve projectile motion.
  • Solving simple problems that involve two bodies connected by a light inextensible string or rod.
  • Modelling bodies moving vertically with constant acceleration.

Momentum

Another major area of physics, you’ll want to begin by understanding the equation of p = mv. For the ENGAA specifically, you’ll need to revise the following:

  • Linear momentum.
  • The principle of conservation of momentum in the 1st dimension.
  • The relation of conservation of momentum to Newton’s laws of motion.
  • Application of the equation “impulse = F∆t”.

Try out our Practice Questions relating to this topic here! 

Energy

This topic is going to require a lot of effort (or energy) to revise, so be sure to revise the following topics:

  • Use of the equations “∆Ep = mg∆h” (gravitational potential energy) and “Ek = 1/2 mv2” (kinetic energy).
  • Use of the principle of conservation of energy, including quantitative and qualitative use of energy conservation.
  • Application of the equations “power = rate of doing work = rate of energy transfer” and “efficiency = (useful energy transfer/total energy input) x 100%”.

Materials

Material physics covers literally all physical matter, but you’re not going to have to know everything thankfully! However, you will need to revise the following: 

  • Application of the equations “density = mass/volume”, “young modulus = stress/strain" and “pressure = normal force/area”.
  • The concepts of tensile and compressive deformation in elastic and plastic.
  • Application of Hooke’s law, including the equation spring constant = force per unit extension.
  • The behaviour of springs, including loads, extension and elastic limit.
  • The concept of strain energy.
  • Definitions of the terms “stress”, “strain” and “ultimate tensile strength”.

Try out our Practice Questions relating to this topic here! 

Waves

In physics, waves are defined as a disturbance that travels through space-time alongside a transfer of energy. For questions based on this topic, you’ll want to revise these topics: 

  • Describing wave motion when illustrated by strong, ropes and ripple tanks.
  • Use of the equations “frequency = 1/period”, “speed = frequency x wavelength” and n = 1/sinC.
  • Identification of nodes and antinodes.
  • The principle of superposition.
  • The comparison of transverse and longitudinal waves.
  • The concepts of reflection/refraction of waves, total internal reflections and critical angle (C).
  • Definitions of the terms “amplitude”, “displacement”, “frequency”, “path difference”, “phase difference”, “period”, “speed” and “wavelength”.

Electricity

This is an area you definitely will be seeing in Section 1A, but advanced physics will test your knowledge even further. Here are the topics you keep an eye out for: 

  • Use of the following equations; “charge = current x time”, “potential difference = work done/change”, “V = IR”, “P = VI”, “P = I2R”, “P = V2/R” and "resistivity = resistance x (cross-sectional area/length)".
  • Application of Ohm’s law and Kirchhoff’s laws.
  • Recognition and use of standard circuit symbols and diagrams.
  • Electromotive force (emf)

Try out our Practice Questions relating to this topic here! 

So that covers all the specific topics that you’ll need to revise! To wind down a little bit, let’s quickly run down something a little more basic!

Many questions will be using scientific quantities and units (SI-units) which you’re going to need to recognise. Makes sure you memorise these SI-prefixes before you enter the exam:

SI-Prefixes/Units

nano- 10–9

micro- 10–6 

milli- 10–3 

centi- 10–2 

deci- 10–1 

kilo- 103 

mega- 106 

giga- 109

These units will be used throughout the entire exam, so make sure you’re using them! For example, your calculations should be done in kilograms rather than grams. 

If you’re eager to read through the official specification for ENGAA, which covers all sections of the assessment, then you can check it out here. 

4/5

REVISION AND EXAM TIPS FOR ENGAA SECTION 1B

With all the required knowledge out of the way, let’s spend some time looking at a few tips and tricks to help you revise and sit the ENGAA like a pro!

Exams Ninja Preparation Pencils Icon

ENGAA Revision Tips

You now know what you need to revise, but what’s the best way to go about it? Here are a few handy tips to get you through Section 1B and beyond!

1. Plan Before You Revise

Any successful engineering student will tell you that creating a revision plan is essential for utilising your preparation time. You’ve got two full subjects to revise and they each cover pretty different topics. While maths is certainly a vital part of physics, your knowledge of trigonometry isn’t too likely to help you with a question on electric circuits. You need to prepare for everything in the ENGAA syllabus, and that’s no easy feat.  

The key to a preparation plan is the schedule, perhaps even planning 6 months in advance. Having times and dates dedicated to each subject and topic will help to keep your revision focussed. Then there’s the matter of how to spread your time across all these different topics, which is really down to your personal needs. We all have weaknesses, so focussing on improving your weaker subjects is a smart idea. For example, you could know pretty everything possible about advanced electricity, but always get caught out with waves. Which one do you think you should spend more time revising? That’s not to say that you should ignore your better topics, you need to maintain your knowledge from all topics, even your best ones.

Of course, you’re not going to be able to work non-stop, and having scheduled downtime will help you avoid procrastinating. Whether you want to set strict times for your breaks or treat them as a reward for accomplishing certain goals, you’ll need to take some time away from your work to refresh and let your revision sink in.  

 

2. Practice Without a Calculator

Remember, you’re not allowed a calculator during any part of the exam! This should be something you’re used to by now, but it’s easy to get used to the convenience of calculators when you have access to them. 

Your preparation time is your chance to break this cycle and get used to solving problems by hand. Sometimes using a calculator is inevitable, but that won’t be the case in the ENGAA. So whenever you get a chance to solve a problem by hand, put that calculator away! You’ll be thankful when you’re breezing through the ENGAA’s questions!

 

3. Complete Practice Questions and Papers

Once you feel confident in your knowledge of the ENGAA’s topics, your next step is to put that knowledge to the test. Of course, practice questions and mock papers are the best way to test yourself without the pressure or consequences of the actual exam.

To get the most of your practice time, you should seek out questions with worked solutions. With these, you’ll be able to fully understand how the question should be worked out. 

Mock exams may feel stressful and unnecessary at first, almost as if you’re forcing yourself to take the exam extra times! But once you’ve gotten through that stress the first time, the exam won’t feel as bad as you’ll have some experience of what to expect.

If you’re looking for a reliable and large collection of practice questions and papers, Exams.Ninja’s ENGAA Preparation Platform is definitely what you want! We have over 900 questions to attempt, so you won’t be running out of practice resources any time soon! 

 

ENGAA Exam Tips

It’s the big day, and you’ve got the dreaded ENGAA paper in front of you. What do you do? Here are a few tricks to help you avoid freezing in your seat!

1. Skip Ahead

Don’t be afraid to skip a question when you need to! Sometimes you’ll find yourself on a question that you just don’t get or can’t quite figure out. That’s alright, but there’s no point spending the whole of the exam trying to get it right. After all, you may be able to answer every question after it and have time to spare. 

That’s not to say you should skip the question entirely of course. While it’s not worth sacrificing the rest of your marks in the paper to get that question right, it’s still worth attempting it if you have time. And if you don’t have time, you should always try to put an answer down, even if it’s a guess! The ENGAA doesn’t have penalties for incorrect answers so you should always try to answer every question! 

 

2. Work Backwards

Remember, all the questions are going to be multiple choice, so you’re always going to have a hint of what your answer should look like when you’re solving it. If you’re not sure where to start, one option is to work backwards with each potential answer and see which answers are definitely incorrect. 

By using the process of elimination, you can easily narrow down your options or find the correct answer. If you believe you have found the correct answer, it’s always worth solving the question normally to double-check that you’ve got it right. 

 

3. Use your Space Wisely

As we’ve mentioned already, your space for working out is limited to what’s available on the question paper. In some cases, this isn’t a lot to work with, so you need to be careful to make the most of what you’ve got. 

Your working out isn’t going to be perfect, so there are going to be mistakes taking up precious space. The key isn’t to avoid these mistakes, as they can be super helpful to your method, but you should try to write as small as possible to utilise your space the most efficiently. 

For questions with graphs or shapes, use them! While these images aren’t going to be to scale, they are super handy for helping illustrate your solutions for yourself. And remember, it doesn’t matter what you write on the question paper as none of that will be marked. The only thing the examiners are going to see is your answer sheet, so don’t be afraid of making silly mistakes in your rough work!    

 

Looking for even more ENGAA Tips and Tricks?

 
 
 
 

The ENGAA Preparation Programme gives you access to all sorts of amazing resources, including life-saving tips and tricks, in-depth revision notes and over 100 expert tutorials, all available from your home! Try it out for free today and see how Exams.Ninja can boost your ENGAA score! 

 
 
 
 
 
 
 
 
 
 
TRY NOW FOR FREE

5/5

ENGAA SECTION 1B PRACTICE QUESTIONS

You should hopefully know by now that practising actual questions is the best way to let your revision sink while preparing your exam technique. Here’s a taste of what you can expect from the ENGAA’s questions.

Exams Ninja Multiple-Choice Questions Icon

ENGAA Advanced Maths Question 1

The variable x is proportional to y cubed; y is proportional to the square root of z. 

If z doubles, x changes by a factor of:

A) √2

B) 2

C) 2√2

D) 3√4

E) 4

 

The correct answer is C.

The two relationships given are: x ∝ y3, y ∝ √z. Therefore, the relationship between x and z is given by:

⇒ x ∝ √z3

Therefore, if z is doubled, then: √23 = 2√2.

 

Check out the ENGAA Algebra and Functions Syllabus.

ENGAA Advanced Maths Question 2

What is the range where x2 < 1/x?

A) x < 0

B) 0 <  x < 1

C) x > 0

D) x >_ 1

E) None.

 

The correct answer is B.

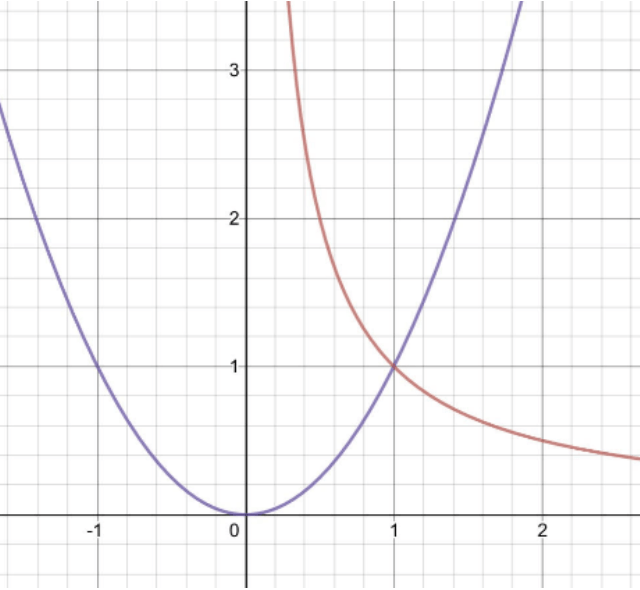
ENGAA Advanced Maths Question 2 Graph

The two graphs have been sketched above. Clearly, the two graphs intersect when x2 = 1/x which is at x = 1. Now we can consider the inequality.

When x > 1, x2 > 1, 1/x > 1.

When x < 1, x2 < 1, 1/x > 1.

In the x < 0 range, the  1/x graph is negative. Therefore, this region does not satisfy the inequality. Thus, the range is 0 < x < 1.

 

Check out the ENGAA Graphs of Functions Syllabus.

ENGAA Advanced Maths Question 3

Which of the following has the largest value for 0 < x < 1?

A) log8(x)

B) log10(x)

C) sin(x)

D) x2

E) ex

 

The correct answer is E.

Firstly, we can approximate the values provided and then compare them with one another:

⇒ log8(x) and log10(x) < 0

⇒ sin(x) ≤ 1

⇒ x2 < 1

⇒ 1 < ex< 2.72.

Therefore, ex is the largest over this range.

 

Check out the ENGAA Exponentials and Logarithms Syllabus.

ENGAA Advanced Maths Question 4

The volume of a sphere is equal to its projected area. What is its radius?

A) 3/4

B) 2/3

C) 1/2

D) 4/3

E) 3/2

 

The correct answer is A. 

The expressions for the volume of the sphere and its projected area, a circle, are equal:

(4/3) πr3 = πr2 ⇒ (4/3)r = 1.

∴ r = 3/4.

 

Check out the ENGAA Geometry Syllabus.

ENGAA Advanced Physics Question 1

What would happen to Vout if the light intensity upon the circuit below is increased?

A) Go up

B) Go down

C) Stay the same

D) Decrease to zero 

E) Increase indefinitely 

 

The correct answer is A.

As the light intensity increases, the resistance of the LDR will decrease. As the potential difference is proportional to the resistance, according to Ohm’s Law, this will increase the share of the potential across the normal resistor. Therefore, Vout will ultimately increase.

 

Check out the ENGAA Electricity Syllabus.

ENGAA Advanced Physics Question 2

 A ball is swung in a vertical circle from a string, of negligible mass, as shown in the diagram. 

ENGAA Section 1B Physics Question 2 Momentum Diagram

What is the minimum speed at the top of the arc for it to continue in a circular path? You may use the formula a = v2/r , where a is the acceleration of a body undergoing circular motion with velocity v and radius r. The acceleration is directed towards the centre of the circle.

A) 0

B) mgr

C) 2r2

D) mg

E) √gr

 

The correct answer is E.

The forces acting on the ball are weight, which is constant and equal to the mass times the gravitational acceleration, and tension T which varies with position. By substituting the expression for acceleration given into Newton’s Second Law, we obtain:

F = ma, a = v2/r

⇒ T + mg = m(v2/r)

The minimum speed at the top of the arc is when it just manages to reach the top, which is when the tension is completely provided by the weight. Therefore, the force keeping the object moving in the circle is instantaneously its weight. Therefore:

T = 0 ⇒ mg = m(v2/r) ⇒ v = √gr.

 

Check out the ENGAA Momentum Syllabus.

ENGAA Advanced Physics Question 3

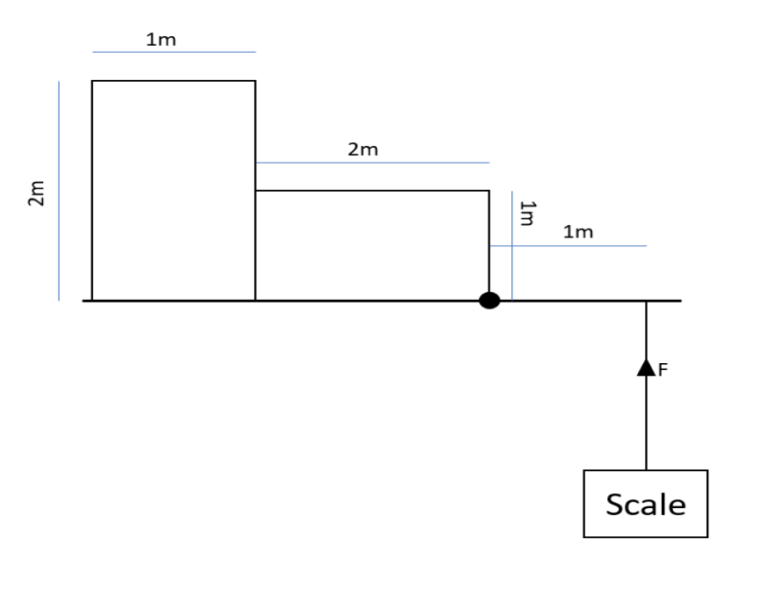
The mechanism below is used to weigh two ridged uniform blocks of dimensions 2 metres by 1 metre, and mass 20 kg, on a lever connected to a weighing scale by a cable. What will the reading on the scale be?

ENGAA Section 1B Physics Question 3 Mechanics Diagram

A) 35kg

B) 40kg

C) 70kg

D) 80kg

E) 90kg

 

The correct answer is C. 

The centre of the mass of the two blocks will be at their geometric centres. So, in this case, that is halfway across each rectangle. The moments can be taken about the black point indicated on the diagram, where the weight of the blocks are used:

1 × F = (1 × (20 × 10)) + (2.5 × (20 × 10)) = 700 N.

This corresponds to a mass of 70 kg and so this will be shown on the scale.

 

Check out the ENGAA Forces and Equilibrium Syllabus.

ENGAA Advanced Physics Question 4

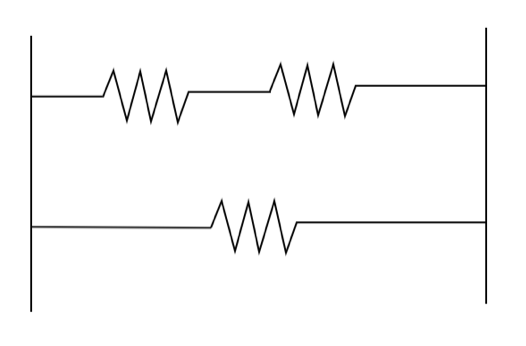
For the arrangement of springs below, what is the spring constant of the whole system, assuming each spring has spring constant k?

ENGAA Section 1B Physics Question 4 Springs Diagram

A) k/2

B) k

C) 2k2

D) 3k/2

E) 2k√3

 

The correct answer is D.

Springs behave like capacitors in series or parallel (the opposite of resistors), so we find the effective spring constant of the springs in series to be: 1/k + 1/k = k2/2k = k/2.

Then, we can add the constant of the parallel spring to obtain 3k/2.

 

Check out the ENGAA Materials Syllabus.

So, with all this knowledge of Section 1B of the ENGAA, you should now have a better understanding of what you’ll need to do in the exam come October!

This is all advanced stuff, so there’s going to be a lot of complex questions in the exam, some of which may trip you up. But that’s OK! At the end of the day, you’re not perfect and the examiners aren’t expecting you to be. With the knowledge you’ve learnt here today and the revision that you’ll be doing from now until the exam, you’ll be able to decrease the number of issues you run into and push through any roadblocks you do encounter! 

Do you want to upgrade your ENGAA revision? Exams.Ninja is just the thing for you!

 
 
 

With the Exams.Ninja ENGAA Preparation Platform, you’ll get to know the exam more intimately than ever before and become an ENGAA genius! When you create and upgrade your account, you’ll have instant access all of to these amazing resources:

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

Training Temple- the home of our essential tips, tricks and tons of expert tutorials (over 100 of them in fact!).

 
 
 
 
 

Practice Dojo- the perfect place to practice your skills, with over 900 exam-quality practice questions, each with a full worked solution to boost your understanding of the topic!

 
 
 
 
 
 
 

Exam Arena- Exams.Ninja has 8 past papers to complete. You’ll get an authentic exam experience alongside an accurate score and worked solutions at the end! 

 
 
 
 
 
 
 
 

So get ready to maximise your chances of success with Exams.Ninja now!

 
 
SIGN UP FOR FREE
Tags: , , , ,