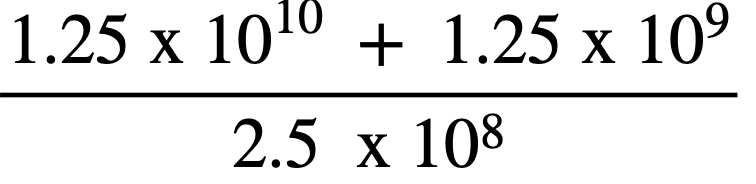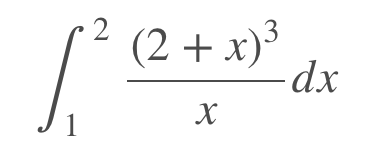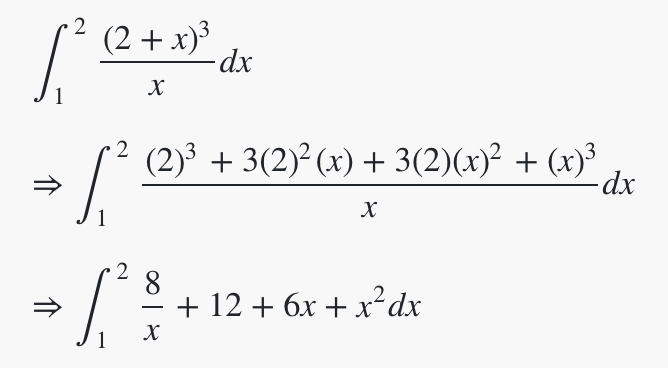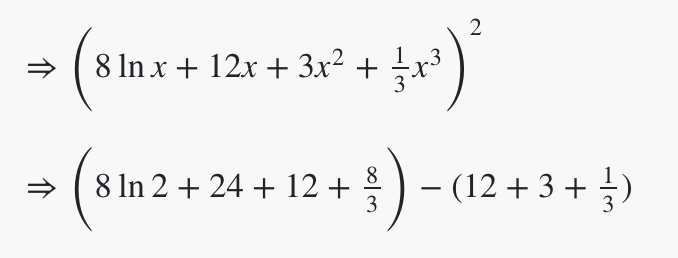ESAT Guides
ESAT Mathematics - What Do You Need To Know?
Written by: Matt Amalfitano-Stroud
The ESAT is a very broad admissions test, featuring 5 subtests covering four separate subjects. In most cases, you’ll be able to choose two of these subtests to complete, but Mathematics is the exception. All applicants must take the Mathematics 1 subtest, so it’s vital that you prepare for it. As well as this, Mathematics 2 is also available for those who want to challenge their mathematical skills further, so this guide will explore everything you need to know for each of these subtests.
1/4
BASICS OF THE ESAT
Before we get our maths hats on, let’s take a moment to refresh our memory on what the ESAT actually is!


What is the ESAT?
The Engineering & Science Admissions Test (ESAT) is an exam used by the University of Cambridge, UCL and Imperial College London as an admissions test for various STEM courses. These include Natural Sciences, Engineering and Veterinary Medicine at Cambridge and a variety of Engineering and Physics courses at Imperial. The ESAT is a pre-interview assessment that can be sat on either October 9th -10th or January 6th – 7th (Cambridge applicants cannot take the January sitting).
The ESAT is designed to test your mathematical and scientific knowledge and to let the admissions team determine your suitability for the university. These courses are demanding and require an in-depth understanding of everything covered within the assessment, so starting your revision now is a great way to ensure you’ll succeed when you’re actually studying at university.
The assessment is made up of 5 subtests, or parts. When you take the test, you’ll usually have to pick two subtests to complete. The options available are Physics, Chemistry, Biology and Mathematics 2. Cambridge Engineering applicants do no have a choice and must take Physics and Mathematics 2.
However, before these subtests, all applicants will be required to take the Mathematics 1 subtest, which features mathematics problems at a GCSE level.
Every subtest of the ESAT features 27 questions, all of which are multiple-choice. Each subtest lasts 40 minutes, leading to a time limit of two hours for the assessment (as you will only be taking 3 subtests). This chart gives a quick rundown of the test format:
ESAT Format Chart
How is the ESAT Scored?
The ESAT is scored on a scale of 1 to 9, with each part being scored separately. This score is determined by the raw marks from each part you completed, with every correct answer increasing your score on the scale. The conversion between raw marks and the final score differs between each part.
There’s no official passing or failing score for the exam, but different colleges within Cambridge will have different scoring standards, so be aware of what they may be when choosing a college. The ESAT is computer-based, meaning there will be no physical answer sheets to fill out. However, it’s recommended you bring a pencil with you as you may still need to complete rough working out on scrap paper. Calculators are not permitted for any part of the test.
More information about ESAT Scoring and Results is available in our dedicated ESAT Results Guide. If you want to find out more about the ESAT, you can check out our Definitive ESAT Guide, which covers everything you need to know about the exam!
Boost your ESAT skills with Exams.Ninja!
With the ESAT Preparation Platform, you’ll be able to use over 100 guides and over 1,200 practice questions to get yourself ready for every part of the ESAT. Start your preparation now by setting up a free account!
2/4
MATHEMATICS 1 IN THE ESAT
The Mathematics 1 subtest in the ESAT is required by everyone who takes the test, so it’s crucial that you’re prepared for everything in the specification. It’s a set of pure mathematics questions that you’ll need to get through, so let’s go through all the mathematical principle you’ll need to be prepared for.
Beyond the assumed mathematics knowledge that is required for Biology, Chemistry and Physics, you’re going to need to know how to answer some pure maths questions for the Mathematics 1 subtest. Let’s go through the Official ESAT Specification to see exactly what you’re going to need to know for it:
Exams.Ninja Tip
Before diving into the specific topics required for ESAT Mathematics, you need to ensure you understand the essential SI prefixes, or Scientific Quantities and Units:
nano- 10–9
micro- 10–6
milli- 10–3
centi- 10–2
deci- 10–1
kilo- 103
mega- 106
giga- 109
Units
We’re starting off with the absolute basics here! You will of course be required to know how to use various units in a mathematical and scientific context. These units range from your basic measures of time, distance and weight, currency, area and volume.
This extends to compound units too, which are units that combine multiple measures into one. Examples include speed, density, pressure, rates of pay and unit pricing. You will need to be able to convert related units in both numerical and algebraic contexts (such as converting seconds into minutes).
Given that this is a science-focused exam, you will also need to have a good understanding of your various scientific units, be it those relating to forces, electricity and more! Those aren’t specific to mathematics however so we’ll need to cover those another time.
Numbers
We can only hope that you’ve learnt how to use standard number functions at this stage in your education! This topic essentially covers your understanding of integers, place values, basic mathematical symbols, exponents, parentheses and the four operations. Part of that will include your understanding of the relationships between operations, particularly the order of operations, otherwise known as PEMDAS.
As a basic example, solve this problem using the correct order of operations:
(17 – 6 ÷ 2)+ 4 x 3
This topic also covers your understanding of fractions, decimals and percentages, as well as your use of the above concepts with them. All of this simply boils down to knowing how to do basic maths!
There are a few terms and slightly more advanced principles to bear in mind too, including negatives, squaring, roots, Pi, surds and rounding. There’s too much to cover everything in detail, but these are all concepts that should be ingrained in your brain at this point!
(FYI: the answer was 26!)
Ratio and Proportion
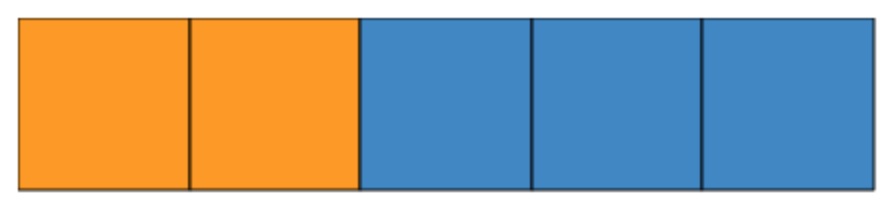
This topic is all about scales and quantities. Ratios in their most basic form are essentially the following:
Here are five blocks, two orange and three blue. The ratio here is 2:3. Of course, this can easily get more complex by adding greater variation and higher quantities. This will then pave the way for concepts such as scale factors, scale diagrams and interchangeable ratios. You’ll also need to be conformable with using ratios alongside fractions, decimals and percentages, plus, of course, the use of ratios in practical, real-world scenarios.
Proportionality could be seen as an even simpler topic. It’s essentially the relationship between different values when manipulated. A linear example could be the increase of a shopping cost as more of an item at the same price is added. The cost of the item and the cost of all the shopping are linked and increase in a proportional manner. Non-linear proportion is much more advanced and goes hand in hand with a topic like geometric manipulation, being used in relation to lengths and areas.
Overall, the concepts at play here aren’t too tricky, the challenge comes more from the values and contexts you’ll be working with.
Algebra
Algebra is where we really start to sink our teeth into the kind of knowledge that’s going to be tested in the exam.
It’s essentially the use of symbols to represent values in a manner that is easier to work with. The questions in the ESAT for algebra can range from finding missing values represented by letters, solving simplifying extended equations into a more understandable format or even representing algebraic equations in a graphic format.
The most essential thing to know for algebra is how values are represented. Here are a few common examples:
ab = a x b
3a = a + a + a
a² = a x a
a/b = a ÷ b
From here, your job is going to be to solve one of the following:
Quadratic Equations
First of all, you’ll definitely need to know the quadratic formula: ax2 + bx + c = 0 (a, b and c represent actual values). You’ll also want to know the formula x = (b ± √b² − 4ac)/2a.
Using this is one of the three ways you can solve a quadratic equation, with the other two being Factorisation and Completing the Square. No matter what method you use, your goal here is usually to work out the missing value in the equation.
Simultaneous Equations
This typically involves manipulating two separate equations to find the common values featured within both, typically represented by x and y. Sometimes you’ll be given one of these values, sometimes you won’t! Take these equations as an example:
3x + y = 10
4x − 3y = 9
There are four steps we need to take to solve this problem. We need to pick a variable to eliminate (for this example we’ll take away y), eliminate said variable, solve the remaining variable and substitute the now known variable back into the equations so we can find y. By taking these steps, we can find that x = 3 and y = 1.
Graphic Questions
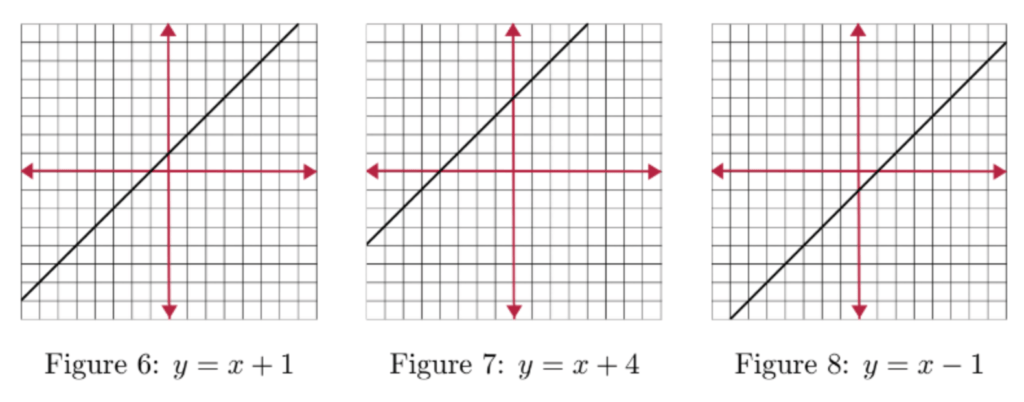
As we mentioned, any algebraic equation can be represented in a graphic form, which is something you’re likely going to have to do in some form for the ESAT. All of the questions are multiple-choice, so you won’t need to actually sketch a graph for a question, but you may need to identify a correct graph or find points on a line. It’s also a handy skill for when you are working out more advanced questions.
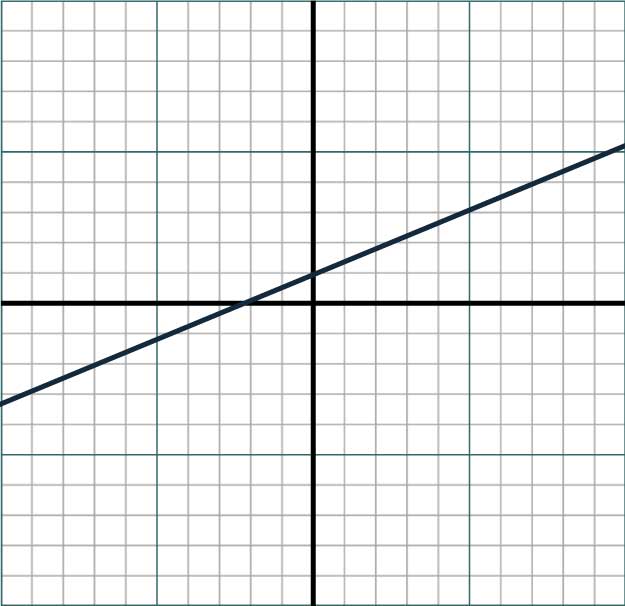
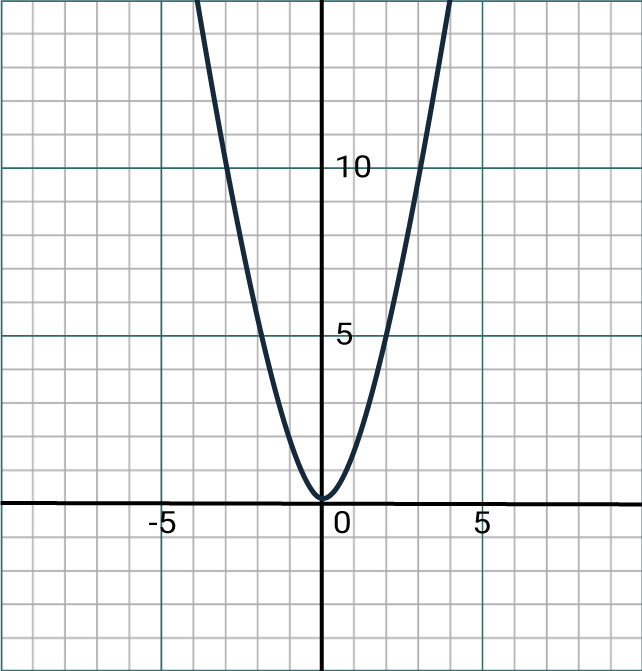
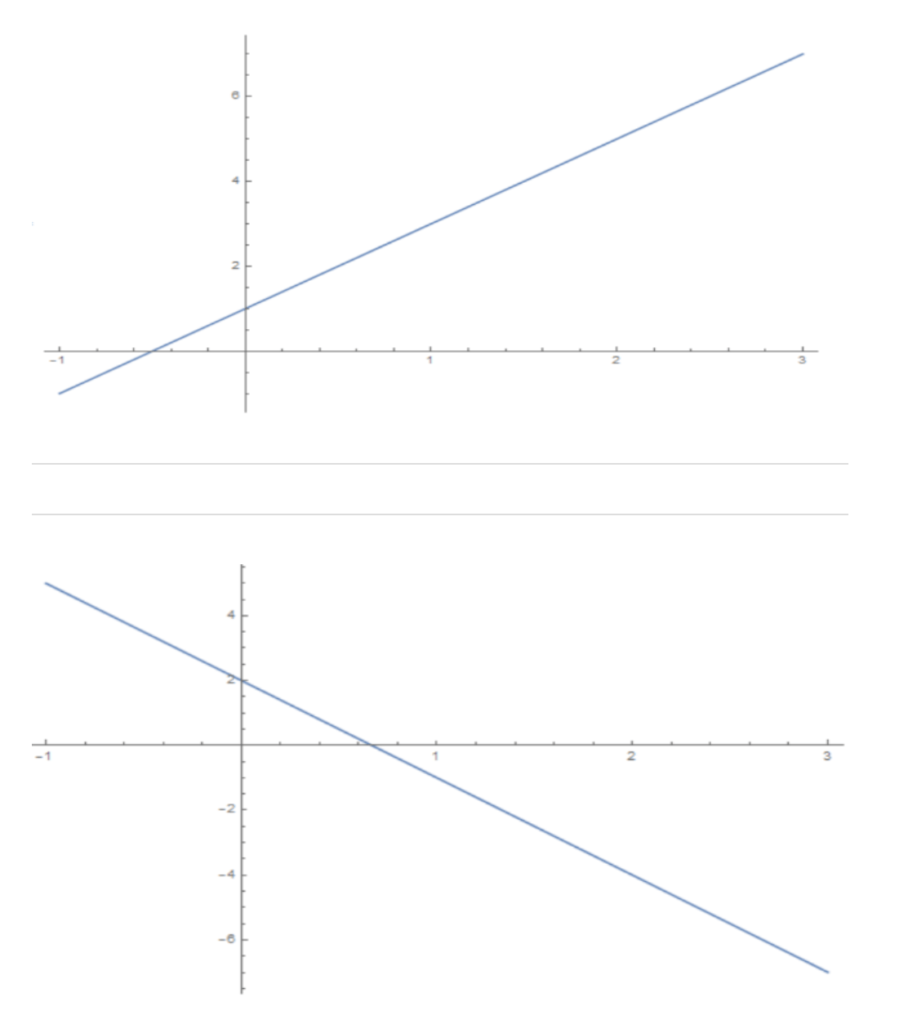
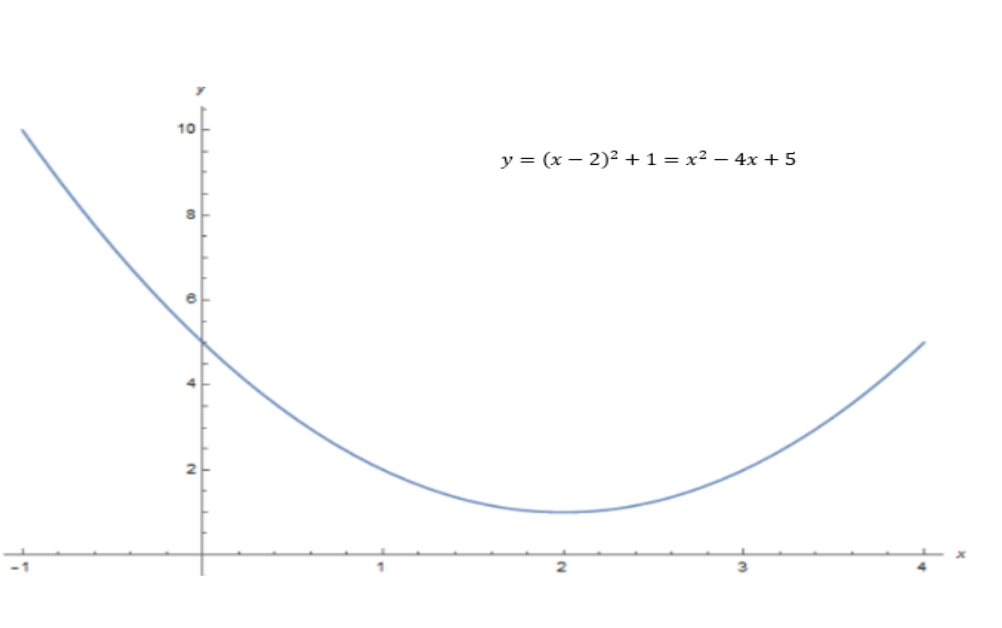
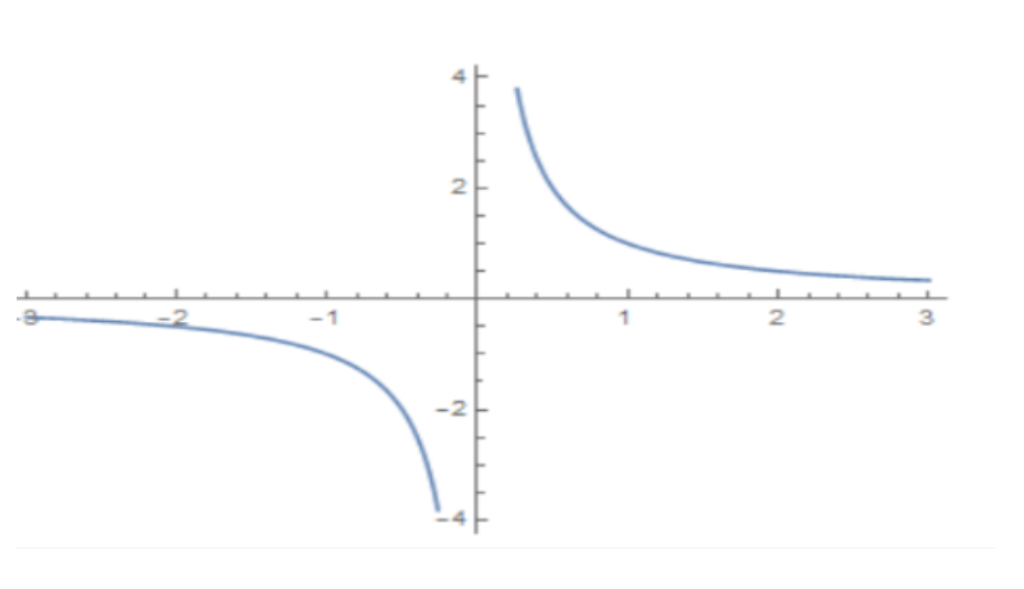
You should expect to find linear and quadratic graphs in these questions, which will typically look something like this:
Linear Graph
Quadratic Graph
Geomerty
Geometry is basically the mathematics of shapes, a favourite for the visual learners out there! You’ll be needing to find angles, perimeters, areas, volumes and more. The most basic rule to remember is that angles of any complete shape add up to 360º.
Different shapes have different rules, the most basic of these being squares and rectangles. The angles here are simple, at 90º in each corner. The perimeter is just a matter of adding all the sides together, while the area = length x width. The same applies to a cuboid, except height will also be included in the equation.
Other shapes such as trapeziums and circles have different rules when it comes to area:
Trapezium – A = 1/2(a + b)h (a and b represent the lengths of the parallel sides of the shape)
Circle – A = πr² (r is the radius of the shape, which is found by dividing the circumference by 2π)
Circles in particular have a very different set of rules, known as Circle Theorem. These relate to the angles, radius and chords that are found within a circle and are essential to know.
Basic trigonometry is also covered in the part of the specification, including knowledge of Pythagoras’s theorem (a² + b² = c²), trigonometric ratios and basic congruence criteria.
Statisitics
Statistics is the mathematics of data. The skills required for this subject are a mixture of interpreting data and representing it in different formats. You’re going to need to be able to read through potentially large amounts of numbers and related data and use what you have available to you to solve problems.
In terms of graphic interpretation of the data, you can expect to see anything from bar charts, line graphs and pie charts. It’s important that you know how to read these and are able to extract pure data from them. You may also need to compare data between two or more different formats in order to come to a single conclusion.
Lastly, you’re going to need to know how to calculate the averages of grouped and ungrouped data:
Mean – m = sum of terms/number of term (essentially the overall value of the data divided by the number of individual pieces of data).
Median – This is the value that fits in the exact centre of the data set, it will likely need to be found by hand at this level as you won’t have too much data to go through.
Range – This is the difference between the highest and lowest values and is simply found by subtracting the lowest value from the highest value.
Mode – the least common of the averages, this is the most frequent value to appear in a data set and will again need to be found by hand.
Probability
This is all about chance. The chance of an event happening under certain circumstances and the chances of multiple events happening together. A key term to understand here is uncertainty, which is what probability seeks to resolve.
Questions on probability will almost always revolve around real-world scenarios, even if it’s something as simple as tossing a coin. Therefore, you’ll need to read the question carefully to ensure you understand every detail that you need to consider.
There are 4 major rules to probability that you should learn:
- Equally Likely Events: If events are equally likely, that means that the probability is a simple split between the different events (for example picking out a red or blue ball from a bag when there are 3 of each colour). A question with this kind of event will likely involve an event that makes things unequal.
- Probabilities must sum to 1: This one’s simple, the values of all your probabilities need to equate to 1, as there is always a 100% chance of one of the potential events happening (at least in the context of an ESAT question).
- Multiple Events: Sometimes you may be asked the probability of multiple events happening. That doesn’t mean two events happening at the same time or one after the other, but rather combining the chances of two potential events into one (for example, the probability of rolling a 1 or 2 on a dice). These would initially be considered as 2 separate chances (e.g. 1/6 chance for each). But with this rule, we would combine the probabilities to 2/6, or simplify to 1/3.
- Conditional Probability: Here, we must consider if a probability is reliant on a separate event. Going back to the red and blue balls example, if 1 red ball were to be taken out of the 6, the probability of then picking out a red ball would be 2/5, and blue 3/5. These probabilities are conditional on the fact that a red ball was initially picked.
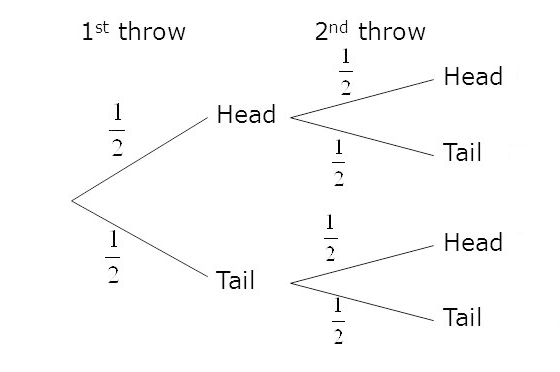
You’ll also need to understand various graphic representations of probability, including Venn diagrams and Tree diagrams (one of which is shown below).
3/4
MATHEMATICS 2 IN THE ESAT
Moving onto the Mathematics 2 subtest of the ESAT, this is where things will really begin to heat up. As well as the maths you’ve just gone through, you’re going to need. to be confident in the use of advanced mathematics. This subtest is usually optional, so only consider it if you’re taking maths at A-Levels (or equivalents), but if you are planning on taking it, read on to learn what’s included in the ESAT specification!



Algebra and Functions
We looked at this topic already, but there’s loads more that we need to consider for advanced maths. Let’s start off with something a bit simpler. We discussed before about the functions within algebra, but in advanced maths, we’re going to need to take into account the Laws of Indices. These essentially show us the functions that can be performed with all rational exponents and intergers, which are represented by n and m:
an x am = an + m
(an)m = anm
an/am = an – m
a0 = 1
a1 = a
a-1 = 1/a
a1/n = n√a
Knowing these will be vital for succeeding in any algebra-based question.
Following on from this, you are also going to need to understand various techniques, including manipulation of surds, solving quadratic inequalities and simplifying polynomials.
it is also important that you understand various basic functions and how they may be used graphically. This is explained below:
- A function can be one-to-one or many-to-one (they cannot be one-to-many). When trying to figure out which way round these are it does help to think of functions as a ‘black box‘ which takes an input (or several) and, as if by magic, gives an output for each of them.
- If a function is one-to-one, one value of x only gives one value of y (for example, the line y = 3x + 2 gives y = 2 when x = 0, and y doesn’t equal 2 anywhere else on the line.
- If a function is many-to-one, lots of values of x can give the same value of y (for example, in quadratic graphs like y = x² ‘inputting’ both 2 and -2 as x would give the same output of 4)
- Things like circles would be examples of one-to-many situations (in a circle centred on the origin with radius 5, the input x = 0 gives an output of both y = 5 and y = -5) – this is not a function as a result – if you were inputting numbers into a computer and it had loads of outputs and ‘didn’t know which it wanted’ that’d usually be pretty unhelpful!
Sequence and Series
This area of maths is, in simple terms, about pattern recognition. A sequence in this context is defined as an ordered list of numbers, worked out by a given formula or relation.
There are two types of sequences that you will need to know about:
Arithmetic Sequence: These are progressions in which the term increases by a fixed amount each time, a, a+d, a+d+d, a+d+d+d, and so on… things like 1, 3, 5, 7, 9…
Geometric Sequence: These are progressions in which the term is multiplied (or divided) by a fixed amount each time, a, 2a, 4a, 8a, and so on… this looks something like 5, 15, 45, 135…
Questions involving either of these will likely be asking you to either find the nth term in the sequence or find the next term.
The other major aspect of this topic is Binomial Expansion, which is an extremely helpful way of finding statistics or approximate expressions without a calculator (which you’re going to need to know considering you won’t have a calculator).
Coordinate Geometry
This is another topic we already had a look at, but there’s still plenty more to be aware of. When we say coordinate geometry, this essentially means two-dimensional, as you will only be working with the x and y planes.
First of all, let’s remind ourselves of some key equations that you’ll need to remember when it comes to graphing:
The Equation of a Straight Line
y = mx + c
Here are a few examples of this equation in action:
We can also use the equations:
y – y1 = m(x – x1)
ax + by + c = 0
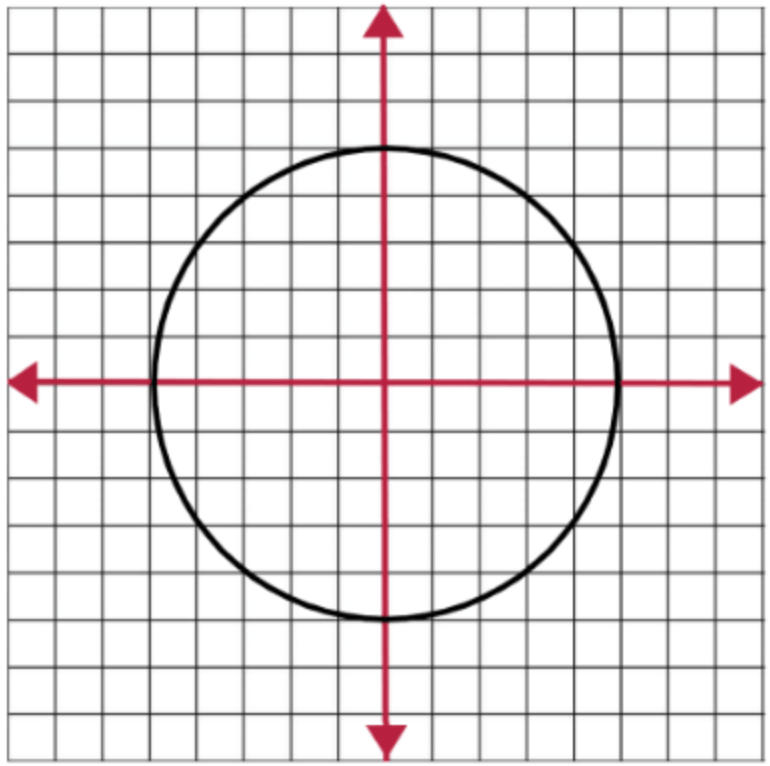
Circle Equation – (x − a)² + (y − b)² = r²
The circle of this equation can be seen below:
We can also use the equation: x² + y² + cx + dy + e = 0
There are various circle properties to understand, including:
a. The perpendicular from the centre to a chord bisects the chord.
b. The tangent at any point on a circle is perpendicular to the radius at that point.
c. The angle subtended by an arc at the centre of a circle is twice the angle subtended by the arc at any point on the circumference.
d. The angle in a semicircle is a right angle.
e. Angles in the same segment are equal.
f. The opposite angles in a cyclic quadrilateral add to 180°.
g. The angle between the tangent and chord at the point of contact is equal to the angle in the alternate segment.
Lastly, be sure to understand how parallel and perpendicular lines work in a geometric context.
Trigonometry
This could be lumped into the same boat as geometry, and in a broad sense they are the same, but trigonometry has so many unique rules and methods that it really needs to be looked at as its own separate thing.
Starting with some basics, you need to be aware of the sine and cosine rules.
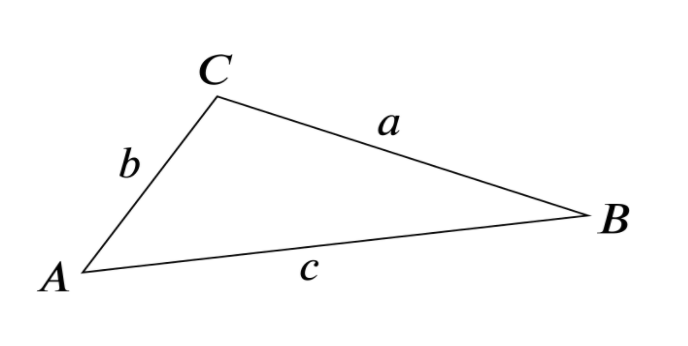
Sine Rule – a/sin A = b/sin B = c/sin C
Cosine Rule – a² = b² + c² – 2bc cosA
We also need to be able to find the area of a triangle using the form 1/2ab sinC. As an example, The area of a triangle ABC shown below is given by 1/2ab sinC = 1/2bc sin A = 1/2ac sin B
You’re also going to need to be aware of Radian Measure, which is the ratio of the circular arc (a) to the radius of the arc (r) in any given part of a circle’s circumference.
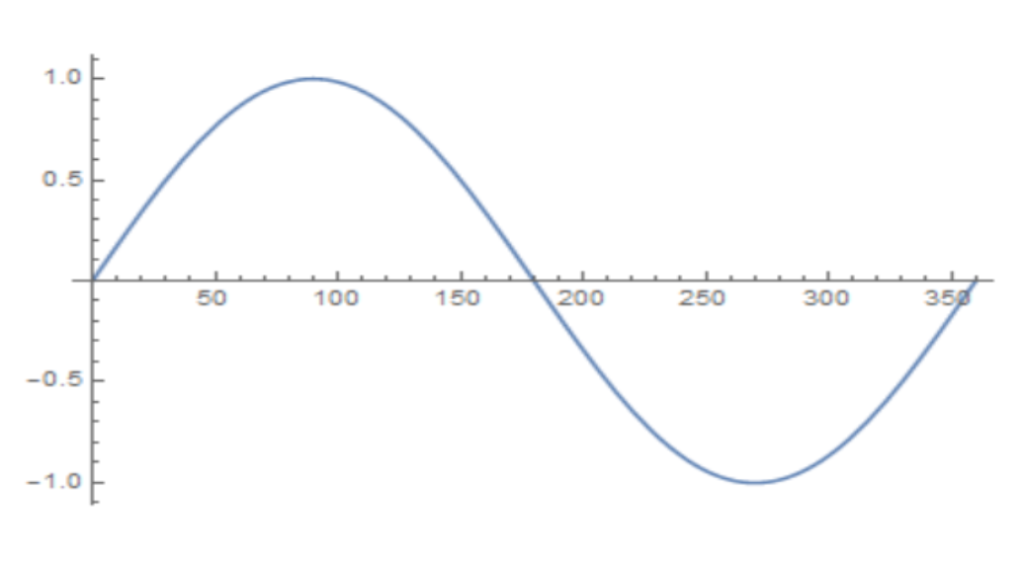
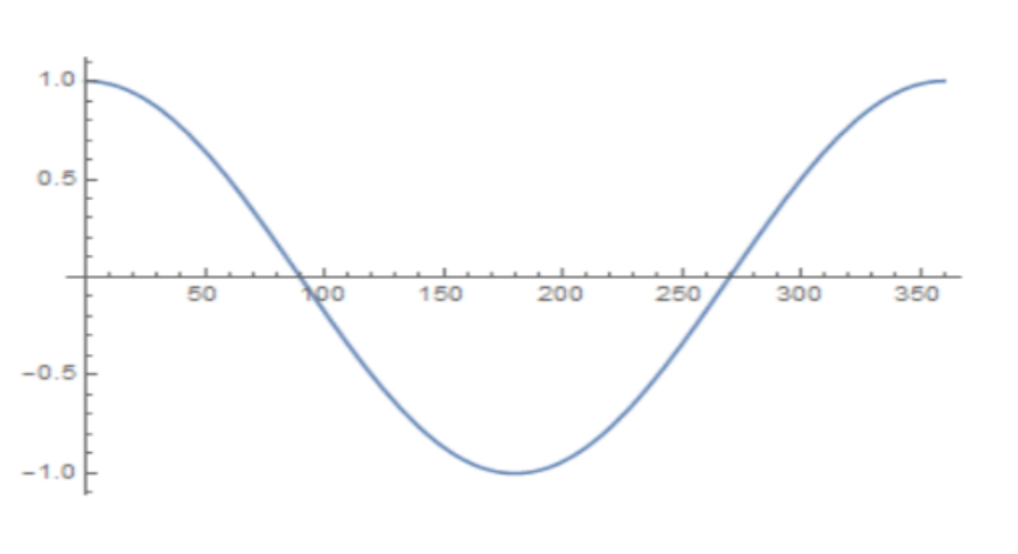
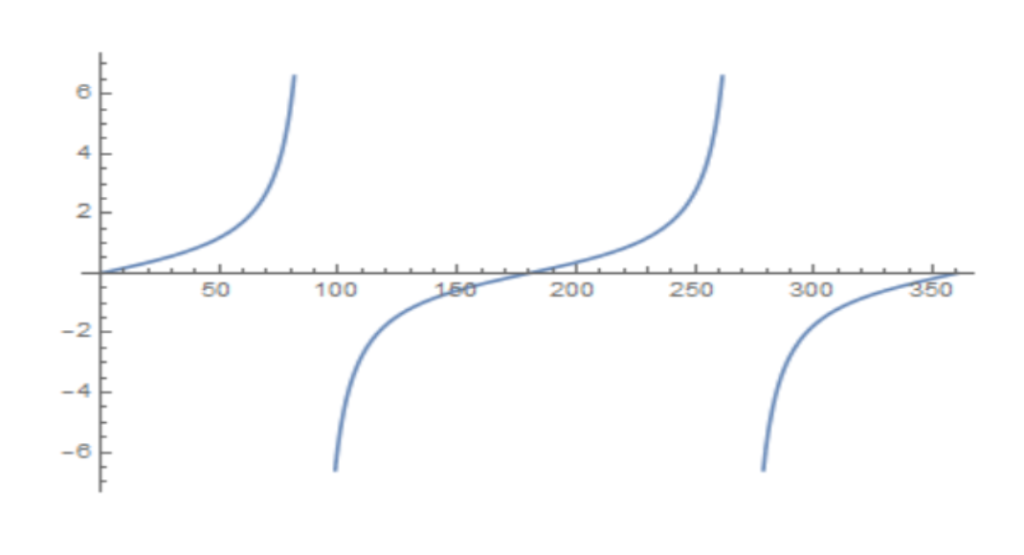
Lastly, you need to know about the Sine, Cosine and Tangent functions. This will include their graphs, symmetries and periodicity. The basics of these functions in regard to a right-angled triangle are as follows:
sinθ = opposite/hypotenuse
cosθ = adjacent/hypotenuse
tanθ = opposite/adjacent
You’ll also need to be aware of the following equations:
a. tanθ = sinθ/cosθ
b. sin²θ + cos²θ = 1
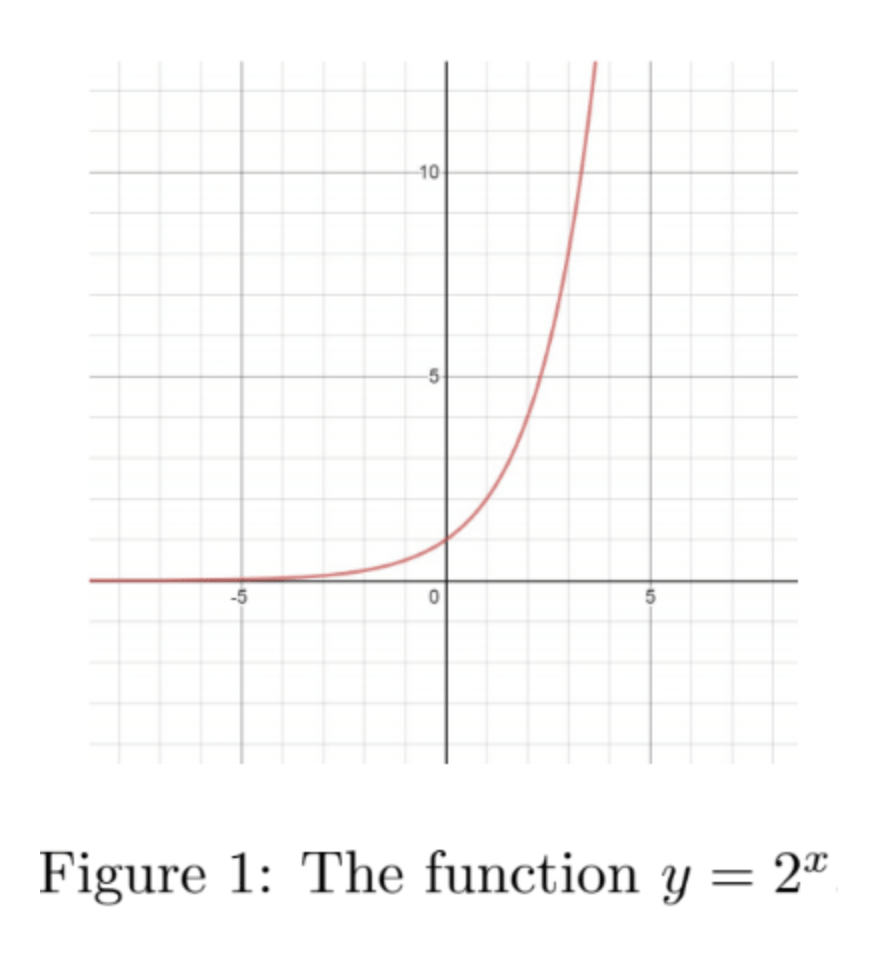
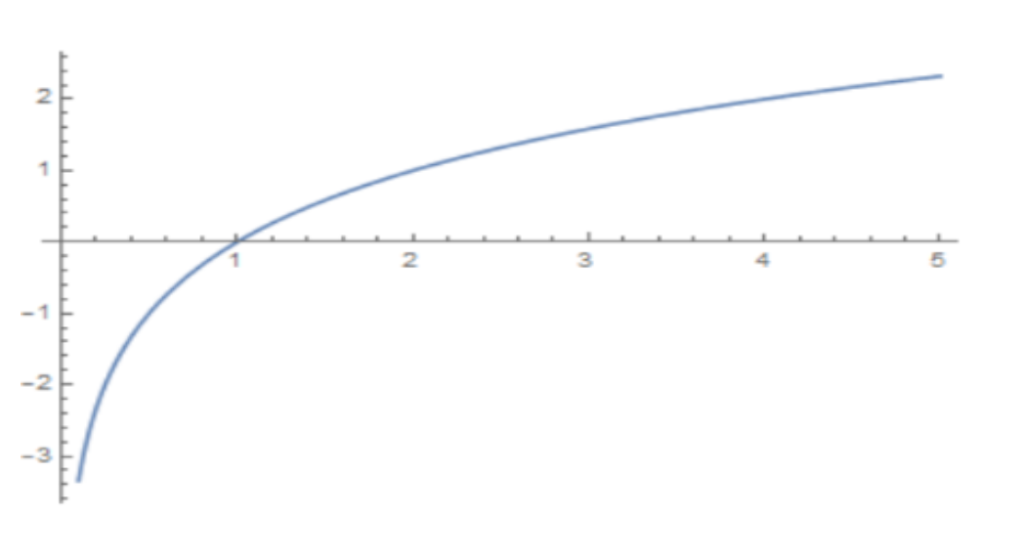
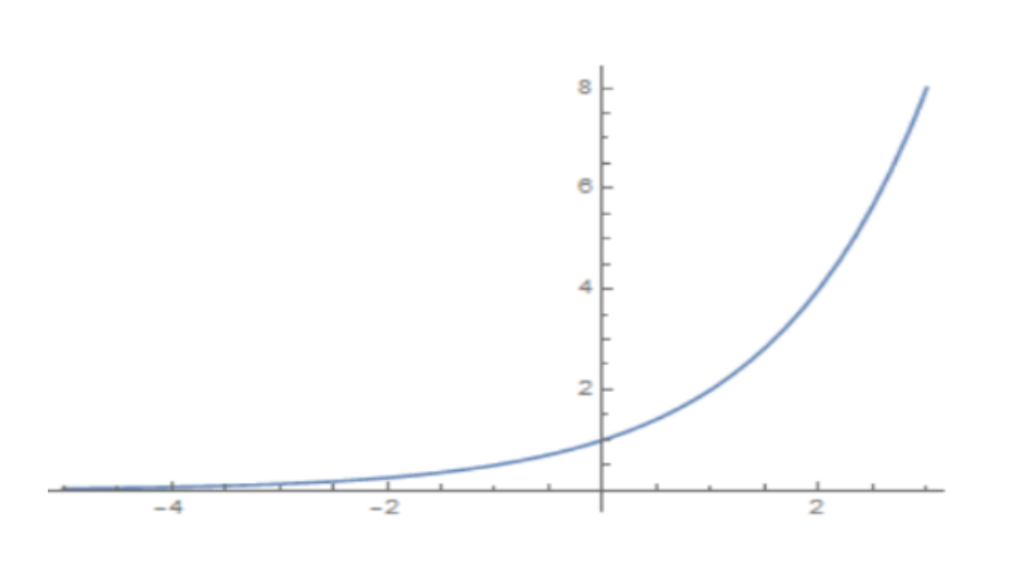
Exponentials and Logarithms
An exponential function is a function of the form y = ax, where ‘a’ can be any positive real number. These can be fairly quickly put into a graph, which you will need to know how to do for simple positive numbers in this case. Take a = 2 as an example:
As for logarithms, you going to need to be familiar with their laws:
ab = c ⇔ b = loga c
Product Rule: loga x + loga y = loga(xy)
Quotient Rule:logax – loga y = loga (y/x)
Power Rule: x loga (y) = loga yx
kloga x = loga(xk)
The are also two special cases to consider:
loga(1/x) = – loga x
loga a = 1
You’ll mostly be using all of this to solve equations, such as 32x = 4 and 25x – 3 × 5x + 2 = 0
Differentiation
Differentiation simply means ‘find the gradient/slope of a curve’ in its most basic sense. It could be described as finding the rate of change in one thing with respect to another.
If we differentiate y with respect to x, the function we get is written as dy/dx.
Often, we have a function written as y = f(x) in which case we also sometimes write dydx=f′(x)
“>dy/dx = f′(x).
One key area you will need to revise is differentiating xn for rational n.
Integration
Integration acts as the reverse of differentiation, as it’s basically completing the process of differentiation backwards. Where you may differentiate x3 to become 3x2, you would integrate 3x2 to become x3, meaning x3 is the integral of 3x2.
One of the first things you’ll need to understand is the notation for integration, which looks like this: ∫f(x)dx
This reads as ‘the integral of the function f(x) with respect to x‘.
Beyond the basics, you’re going to need to understand and be prepared for the Fundamental Theorem of Calculus, the Trapezium Rule, Differential Equations and the ability to interpret definite and indefinite integrals.
Graphs of Functions
Graphs of functions have been a theme throughout a lot of what we’ve spoken about, but we’ll quickly refresh our memory on what they look like to finish things off.
Line Graphs
Quadratic Graphs
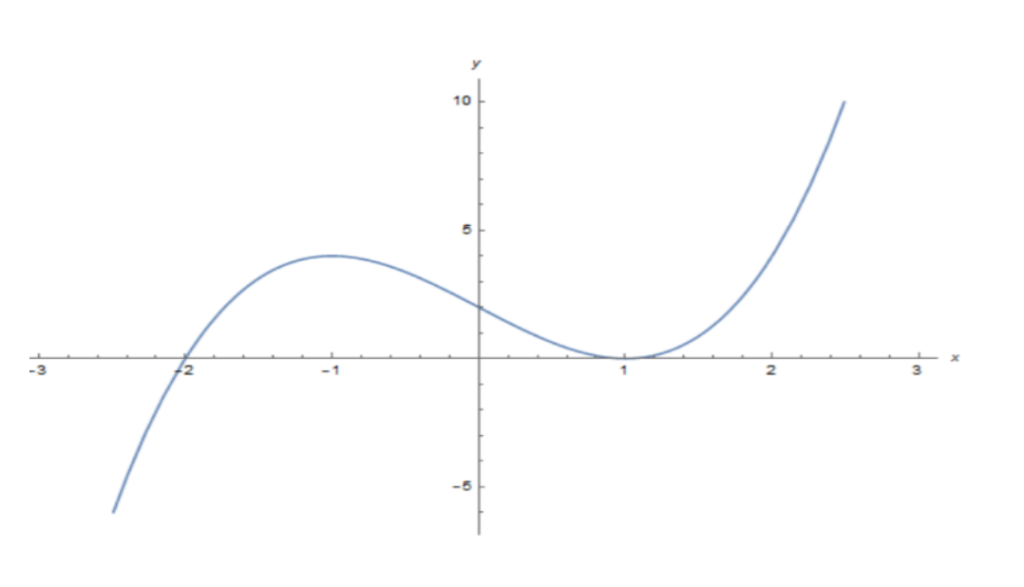
Polynomials Graphs
This graph represents the polynomial y = (x−1)2(x+2).
y = sinx
y = cosx
y = tanx
y = log²x
y = 2x
y = 1/x
Remember the four major types of graphic transformations as well:
- y = af(x) – stretch of scale factor aa in the y direction.
- y = f(x) + a – translation of aa in the positive y direction.
- y = f(ax) – stretch of scale factor 1/a in the x direction.
- y = f(x + a) – translation of scale factor −a in the positive x direction.
That covers everything that you’re going to need to know for the ESAT, at least in terms of pure mathematics.
Don’t forget, there are three whole sciences that are covered too, so be sure to plan out your revision so you have time to look at everything included in the subtests you plan to complete!
Still unsure about what you need to know for the ESAT?
The ESAT.Ninja Preparation Platform provides you with over 100 expertly written tutorials that cover everything you need to know about ESAT mathematics and science, as well as plenty of amazing revision and exam tips!
Start your ESAT revision with Exams.Ninja today and boost your chances of success!
4/4
ESAT MATHS PRACTICE QUESTIONS
To finish off this guide, let’s look at a selection of practice questions from Mathematics 1 and Mathematics 2 in the ESAT. Work through these examples to get a taste of what to expect in the real test.
ESAT Mathematics 1 Question 1
Calculate the following:
A) 0
B) 1
C) 55
D) 110
E) 1.25 x 108
F) 5.5 x 107
G) 5.5 x 108
The correct answer is C.
Let y = 1.25 x 108; this is not necessary, but helpful, as the question can then be expressed as:
(100y + 10y)/2y = 110y/2y = 55
ESAT Mathematics 1 Question 2
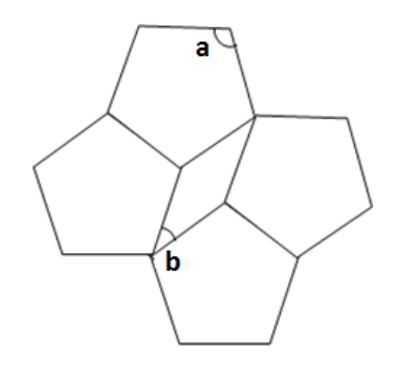
The diagram to the right shows a series of regular pentagons. What is the product of angles a and b?
A) 580º
B) 1,111º
C) 3,888º
D) 7,420º
E) 9,255º
The correct answer is C.
Remember the interior angles of a pentagon add up to 540° (three internal triangles), so each interior angle is 540/5 = 108°. Therefore angle a is 108°. Recalling that angles within a quadrilateral sum to 360°, we can calculate b. The larger angle in the central quadrilateral is 360° – 2 x 108° (angles at a point) = 144°. Therefore the remaining angle, b = (360 – 2(144)]/2 = 36°. The product of 36 and 108 is 3,888°.
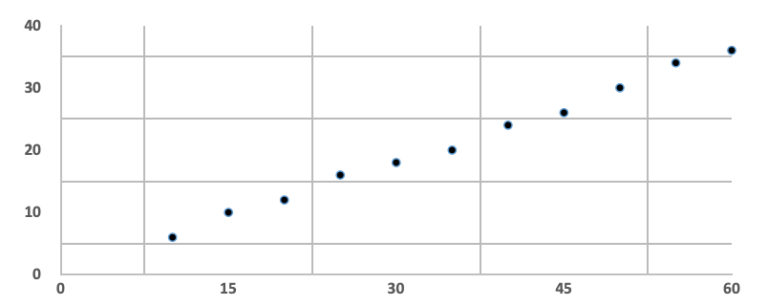
ESAT Mathematics 1 Question 3
What is the equation of the line of best fit for the scatter graph below?
A) y = 0.2x + 0.35
B) y = 0.2x – 0.35
C) y = 0.4x + 0.35
D) y = 0.4x – 0.35
E) y = 0.6x + 0.35
The correct answer is E.
Begin by drawing your line of best fit, remembering not to force it through the origin. Begin fitting the general equation y = mx + c to your line. Calculate the gradient as ∆y/∆x and read the y intercept off your annotated graph.
ESAT Mathematics 1 Question 4
The table below shows the results of a study investigating antibiotic resistance in staphylococcus populations.
A single staphylococcus bacterium is chosen at random from a similar population. Resistance to any one antibiotic is independent of resistance to others. Calculate the probability that the bacterium selected will be resistant to all four drugs.
A) 1 in 1012
B) 1 in 106
C) 1 in 1020
D) 1 in 1025
E) 1 in 1030
F) 1 in 1035
The correct answer is D.
The key here is to note that the answers are several orders of magnitude apart so you can round the numbers to make your calculations easier:
Probability of bacteria being resistant to every antibiotic = P (Res to Antibiotic 1) x P (Res to Antibiotic 2) x P (Res to Antibiotic 3) x P (Res to Antibiotic 4)
=100/1011 x 100/109 x 100/108 x 10/105
=108/1033 = 1/1025
ESAT Mathematics 2 Question 1
Evaluate the value of the following integral:
A) 8 ln 2 + 70/3
B) 3/2 − ln 2
C) In(1/2)
D) In 2 – 11/3
E) 2 In 3 – 7/3
The correct answer is A.
To compute this integral, you need to rewrite it by expanding the bracket term in the numerator.
Now this can be evaluated. The only term you may be unfamiliar with is the first – here, we have to use the “In” trick. If the numerator is the derivative of the denominator, the integral is just the log of the denominator.
This is easy to evaluate and gives a result of 8 In 2 + 70/3.
ESAT Mathematics 2 Question 2
What number should be added to each of the three numbers 3, 11 and 27 so that the resulting numbers form a geometric sequence?
A) 2
B) 3
C) 4
D) 5
E) 6
The correct answer is D.
For a geometric sequence a,b,c: b = √ac
Assuming that x is the value that needs to be added, the resulting sequence would be: 3 + x, 11 + x, 27 + x. Applying the property of a geometric sequence:
11 + x = √(27 + 3)(3 + x) → 121 + 22x + x2 = 81 + 30x + x2 → x = 5 → solution (d)
ESAT Mathematics 2 Question 3
Which of these expressions is strictly positive in the range π/4 < x < 3π/4?
A) cos(2x)/sin (2x)
B) (tan(x))3
C) In(x)
D) 1/arctan(x – 1/2)
E) None of the above
The correct answer is D.
We disregard A because cos(x) is negative between π/2 and 3π/2, whereas sin(x) is positive and negative in this range, meaning there is a range of values between π/4 and 3π/4 for which cos(2x)/sin(2x) is negative.
We disregard B because tan(x) is negative between π/2 and 3π/4 thus (tan(x))3 will be negative in this range too.
We disregard ln(x) because it is negative for x<1 ; π/4 is < 1.
arctan(x) is positive for x > 0, and so 1/arctan(x) is positive in this range too. Whilst 1/arctan(x – 1/2) is only positive for x > 1/2, π/2 > 1/2, thus arctan(x – 1/2) is positive for the required range.
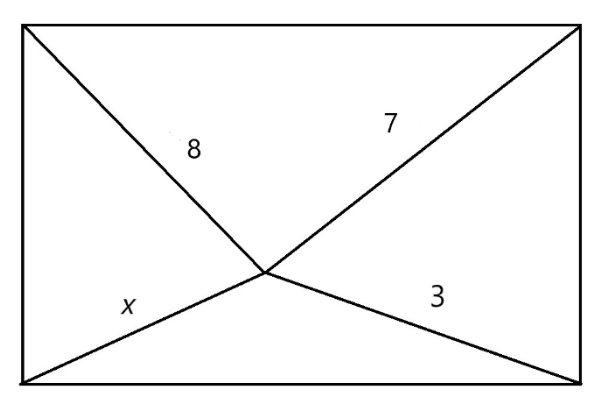
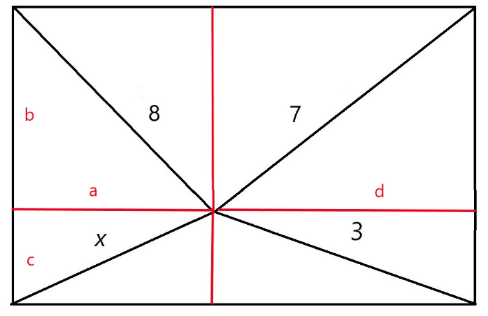
ESAT Mathematics 2 Question 4
The diagram below is a rectangle, with lines connected from its corners. The length of each line is labelled.
Determine the length of x.
A) x = 2√6
B) x = 4√3
C) x = 4√2
D) x = 2√5
E) x = 2√3
The correct answer is A.
We have to break the rectangle into smaller rectangles in order to solve the problem.
Now, we can use Pythagoras’s theorem on all of these triangles.
a2 + b2 = 64, a2 + c2 = x2
b2 + d2 = 49, c2 + d2 = 9
To solve for x, we must take away the second equation from the first and the fourth equation from the third to obtain:
a2 + b2 – (a2 + c2) = 64 – x2
⇒ b2 – c2 = 64 – x2
b2 + d2 – (c2 + d2) = 49 – 9 = 40
⇒ b2 – c2 = 40
Now, we can equate the two expressions to solve for x:
⇒ 64 – x2 = 40
⇒ x2 = 24
⇒ x = 2√6
We hope these practice questions have helped you start to understand what you should expect in the ESAT. You can also keep an eye out for more ESAT practice questions on Exams.Ninja coming soon!
So, that’s pretty much everything covered by the ESAT specification for assumed mathematical knowledge! The majority of these topics should be pretty well known to you by now but it’s always good to have a general refresh, especially when considering the context of the ESAT itself.
Don’t forget to prepare for the sciences as well, though it’s best to choose your subtests well in advanced so you don’t spend too much time revising for a subtest you won’t actually complete. How you revise is up to you, but we wish you the very best of luck!
Imagine a platform with everything you need to revise for the ESAT…
Imagine no more, because that’s exactly what the ESAT.Ninja Preparation Platform provides you with! Here are some of the amazing features you can expect to find when you sign up:
Training Temple- exclusive tips, amazing revision notes and over 100 expert tutorials to guide you every through everything you’ll need to revise.
Practice Dojo- take on over 1,200 practice questions that cover every part of the assessment. Each one provides fully worked solutions to leave no questions unanswered!
Exam Arena- Attempt our collection of ESAT mock papers and NSAA & ENGAA Past Papers in a simulated exam scenario. You’ll get an accurate score and you’ll be able to try again as many times as you need!
Start your ESAT preparation today and become an ESAT Master!